مساحة الدائرة

اضغط هنا لمشاهدة البرمجية

الهدف العام : إجادة حساب مساحة الدائرة

الأهداف التفصيلية:

التعرف على قانون حساب مساحة الدائرة.

استخدام مساحة متوازي الأضلاع في إيجاد مساحة الدائرة .

تحديد طول محيط الدائرة .

شرح البرمجية وخطوات العمل:

 النقطة الحمراء الموجودة أعلى الرسم الأول إلى اليسار تستخدم لتحريك شكل الدائرة.

النقطة السوداء الموجودة أسفل رسم الدائرة تستخدم لتوضيح الأبعاد

.

إيجاد مساحة الدائرة

·         المطلوب إيجاد الدائرة الموجودة بالرسم الأول.  

·         حرك النقطة الحمراء الموجودة أعلى الرسم الأول إلى اليسار.

·         لاحظ من الرسم الثاني أن مساحة الدائرة تم تقسيمها إلى عشر مثلثات متطابقة.

·         لاحظ من الرسم الثاني أن المثلثات متساوية المساحة وكل منها متساوي الساقين كل من ضلعي

المثلثات يساوي نصف قطر الدائرة كما بالشكل .

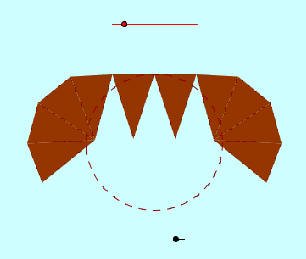
·  حرك النقطة الحمراء الموجودة أعلى الرسم حتى المنتصف والنقطة السوداء الموجودة أسفل الرسم إلى نهايتها كما هو موضح بالشكل الثالث .

·         لاحظ أن مجموع أطوال قواعد العشر مثلثات يساوي طول محيط الدائرة وأن ارتفاع المثلثات متساوي وكل منهم ارتفاعه يساوي نصف قطر الدائرة كما هو مبين بالرسم الثالث.

·         حرك النقطة الحمراء الموجودة أعلى الرسم قرب النهاية .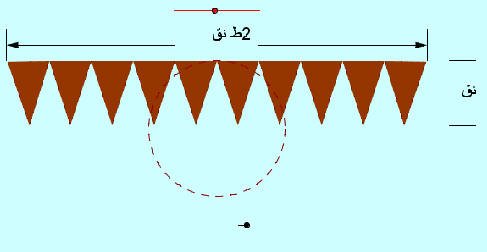

·         لاحظ أننا نقوم بإنشاء عشر مثلثات ذات لون قاتم تتطابق مع العشر مثلثات الأساسية  .

·         حرك النقطة الحمراء الموجودة أعلى الرسم حتى نهايتها.

·         لاحظ أن الشكل المتكون من اتحاد المثلثات (20 مثلث ) عبارة عن متوازي أضلاع  .

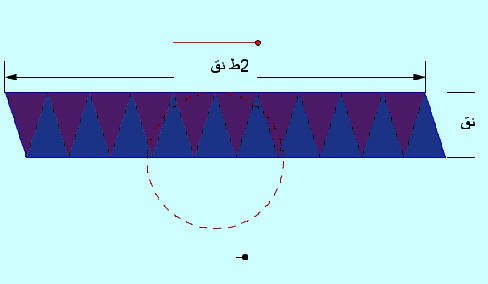
·         لاحظ أن طول قاعدة متوازي الأضلاع المتكون عبارة عن مجموع أطوال عشر مثلثات ويساوي طول محيط الدائرة(2 ط نق ( وارتفاعه يساوي طول نصف قطر الدائرة ( نق ) .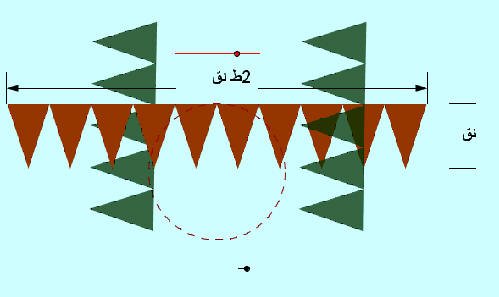

·         أوجد مساحة متوازي الأضلاع مستخدماً القانون مساحة متوازي الأضلاع = طول القاعدة × الارتفاع الساقط عليها

  .نستنتج من ذلك أن مساحة متوازي الأضلاع=2ط نق×نق

 ·        نستنتج من ذلك أن مساحة متوازي الأضلاع = 2 ط نق²

·       لاحظ أن مساحة الدائرة تساوي مساحة عشر مثلثات فقط.

·        بناءاً على ذلك تكون مساحة الدائرة تساوي نصف مساحة متوازي الأضلاع.

·        بناءاً على ذلك تكون مساحة الدائرة = ط نق².

المادة العلمية:  مساحة الدائرة = ط نق²