مكعبات متداخلة

المكعبات المتداخلة

واجهة البرنامج:

تتكون واجهة البرنامج من مساحة للعمل في الجهة اليسرى وبعض الازرار في الجهة اليمنى موزعة كما يلي:

1- نجد في اعلى الجهة اليمنى منطقة قاتمة اللون(نسميها المخزن) تكون فيها المكعبات (ثلاثة) ولكن على شكل مربعات لسهولة التعامل معها ولاخذ أي واحد منها نؤشر عليه بالفأرة ونسحبه الى المكان الذي نريده في ساحة العمل ثم نفلته فيظهر على شكل مربع منقط دلالة على انه نشِط ولالغاء تنشيطه نضغط في اي نقطة خارجة عنه فيصبح في الوضع الطبيعي ولتنشيطه مرة اخرى نضغط عليه .

2- في الجهة اليمنى مجموعة من الازرار الملونة عند الضغط على أي منها يتم تلوين المكعب النشط حسب اللون المراد ، واذا لم يكن أي شكل نشطا فانه يتم تحويل اللون الى مخزن المكعبات.

3- تحت الالوان يوجد مؤشر ازرق اللون يتحرك رأسيا لتكبير المكعبات في منطقة العمل.

4- اسفل مؤشر التكبير يوجد زر وكما هو واضح فانه يستخدم لمسح منطقة العمل كاملة

ملاحظات مهمة للعمل في البرنامج :

أ) يوجد في البرنامج امكانية تجميع عدد من الاشكال في شكل واحد بحيث يتم تحريكة وتلوينه كانه شكل واحد ، ويكون ذلك بالضغط على الفأرة قريبا من الاشكال المراد تجميعها ثم سحب الفارة فيتكون خلال عملية سحب الفارة شكل مستطيل يشمل جميع الاشكال ، بعد ذلك نترك الفارة لتتم عملية التجميع ، ولا يمكن التراجع عن هذه الخطوة فكن على حذر عند استخدامها.

ب) عند وجود مكعب زائد في مساحة العمل يمكن التخلص منه بوضعه على أي مكعب موجود في مساحة العمل أو تجميعه معه في شكل واحد.

ج‍) يمكن تدوير أي شكل أو مجموعة من الاشكال فعند اقتراب الفأرة من ركن أي شكل تظهر نقطة سوداء كبيرة على الركن وبالضغط على الفأرة وتحريكها يتم تدوير الشكل سلبا أو ايجابا.

د ) اذا لم تظهر واجهة البرنامج كاملة على الشاشة يمكن الضغط بالفارة على أي مكان خارج لوحة العمل ومن ثم الضغط على زر (F11) في اعلى لوحة المفاتيح والعودة بنفس الطريقة.

استخدامات المكعبات المتداخلة :

يوجد العديد من المفاهيم الرياضية والمنطقية التي يمكن تعلمها باستخدام هذه المكعبات والتي لا يمكن حصرها وتعتمد على قدرات وخيال المتعلم في تسير معه الى مالا نهاية .

(1)- استخدام المكعبات في البناء والتصنيف باللون والشكل والمقارنة وتركيب عدة اشكال مختلفة.

(2)- مكونات العدد عشرة وتطبيق عمليتي الجمع والطرح عليها كما في الشكل التالي:

من خلال الشكل يتعلم الطالب كيف ان 1+9 = 10 ، 2+8 = 10 ، ... وهكذا

ثم يتعلم 10-3 = 7 ، 10-4 = 6 ، ... وهكذا

(3)- دراسة عمليات التناظر حول محور ( اللون الاصفر) وحول نقطة( اللون الازرق) والدوران (اللون الاخضر) كما نراه في الشكل التالي:

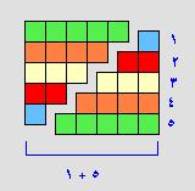
(4)- يمكن اثبات ان مجموع الاعداد الصحيحة 1 +2+3+4+ ....+ ن

يساوي ن(ن+1)÷2 كما يوضح الشكل التالي :

(5)- تمثيل العدد بأكثر من صورة كما يتضح مع العدد 12 :

(6)- عملية الجمع البسيط فيما دون المائة وكذلك الطرح بنفس الطريقة (اضافة أو طرح مكعبات ) :

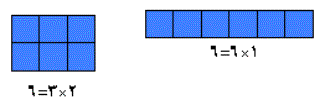
(7)- الضرب :

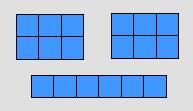
تتلخص عملية الضرب في المكعبات بتكوين مستطيل ابعاده العددين المضروبين ، ثم نكمل انشاء المستطيل وتكون المكعبات التي يحتوى هي ناتج الضرب والشكل يبين حاصل ضرب 2×3=6 و 1×6=6 .

(8)- القسمة :

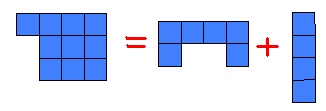
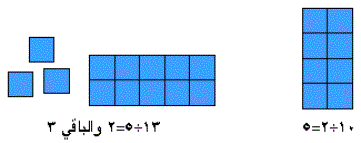
بالنسبة لعملية القسمة فانها بنفس الطريقة السابقة للضرب ولكن نقوم بتمثيل المقسوم ثم محاولة انشاء مستطيل قاعدته هي المقسوم عليه فيكون الارتفاع هو ناتج القسمة وباقي المكعبات التي لاتتمم المستطيل هي الباقي ، والشكل يبين حاصل العمليتين :

10÷2=5 وَ 13÷5=2 والباقي 3

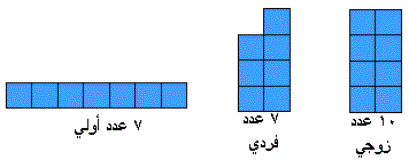
(9)- الأعداد الزوجية والفردية والأولية :

تقوم فكرة تمثيل العدد الزوجي بتكوين مستطيل من العدد عرضه 2 ، والعدد الذي لا يمكن تمثيله بهذا المستطيل يكون فرديا .

وبالنسبة للعدد الأولي فانه العدد الذي لا يمكن تكوين مستطيل منه إلا على شكل سلسلة عرضها الوحدة فقط مهما كانت طريقة تكوين العدد .

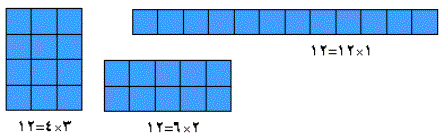
(10)- القواسم العدد :

قواسم العدد هي العوامل الناتجة من تمثيل العدد بكل صورة ممكنة

فمثلا العدد 12 قواسمه : 1 ، 2 ، 3 ، 4 ، 6، 12 .

لأن 12= 1×12 = 2×6 = 3×4

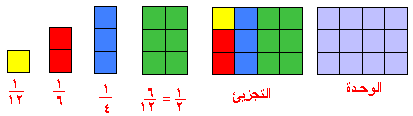
(11)- الكسور :

يسهل التعامل مع الكسور باستخدام المكعبات على اعتبار ان شكلا ما هو الوحدة ومن ثم نستطيع دراسة اجزاء هذا الشكل كما هو موضح ادناه .

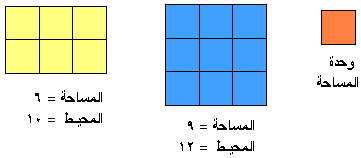
(12)- المحيط والمساحة :

نستطيع من خلال البرنامج والمكعبات دراسة المحيط والمساحة بكل وضوح وخصوصا المربع والمستطيل