اللوحةالهندسية

اللوحة الهندسية المربعة :

هي عبارة عن لوحة مربعة الشكل عادة لها مسامير على مسافات متساوية أفقيا وعموديا ومنتظمة على شكل شبكة مربعة . وتستعمل المطاطات المشدودة بأطراف المسامير لتمثيل الأشكال الهندسية ودراسة بعض المفاهيم الرياضية مثل المحيط والمساحة والتوازي وغيرها.

واجهة البرنامج:

كما هو موضح على الصورة التالية :

طريقة العمل :

نسحب أي مطاط من المخزن إلى أي مسمار نريده بالضغط المتواصل على زر الفأرة ثم نتركه عند المسار المحدد فتلاحظ وجود مطاط معاق على المسمار ، ننشط المطاط بالضغط على أي طرف منه ليصبح لونه ازرق ، ثم نسحب طرفه إلى أي نقطة أخرى نريدها فيصبح لدينا خط مستقيم ومن أي نقطة علي المطاط نسحب المطاط ونضع طرفه على أي مسمار فيتكون لدينا شكل مثلث وإذا أردنا تلوينه نختار أحد الألوان بالضغط عليه فقط ،وهكذا باقي الأشكال الهندسية.

ملاحظة مهمة للعمل :

(*) قد لا تظهر اللوحة بشكل كامل على الشاشة ، ولذلك لابد من الضغط بالفارة على أي نقطة خارج لوحة العمل ومن ثم ضغط الزر ( F11 ) الموجود في أعلى لوحة المفاتيح لتأخذ مساحة العمل كامل الشاشة.

مميزات البرنامج :

(*) إذا أردنا تحرير(إفلات) المطاط من أي نقطة نريدها نضغط على أحد الزرين ( Ctrl , Shift ) باستمرار ونؤشر على المسمار بالفأرة فيتحرر المطاط من المسمار ، وإذا أردنا حذف شكل كامل نضغط على الزر مسح ( Delete ) في لوحة المفاتيح أو الزر مسح في لوحة البرنامج ليمسح كامل المطاطات على اللوحة.

(**) من خواص الزر قياسات على لوحة العمل انه إذا كان الشكل المرسوم يمثل شكلا هندسيا فانه بالضغط عليه يحسب لنا محيط ومساحة الشكل وإذا كان الشكل المرسوم عبارة عن مستقيم فانه يحسب لنا طول القطعة المستقيمة وميلها .

استخدامات اللوحة الهندسية :

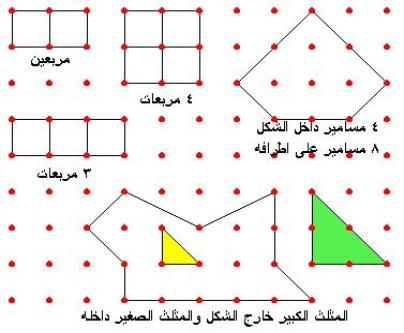
(1)- التسلية ورسم أشكال هندسية مختلفة كما هو واضح أدناه :

(2)- العد ، مفهوم داخل وخارج الشكل ، المقارنة :

عند تكوين شكل ما مغلق يمكن دراسة مفهوم داخل وخارج الشكل، ومفهوم الأكبر والأصغر كذلك يمكن استخدام اللوحة لتكوين أي شكل مستطيل أو مربع وعد المربعات داخله .

أو تكوين أي شكل هندسي مغلق وعد المسامير التي داخل الشكل أو التي على أطراف الشكل.

(3)- مفهوم المساحة والمحيط :

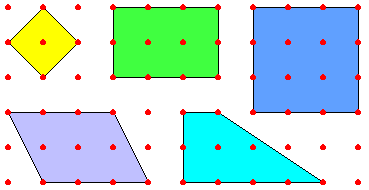
من خلال البرنامج نستخدم اللوحة الهندسية لدراسة المحيط والمساحة باعتبار أن كل مسافة بين نقطتين تمثل وحدة طول واحدة ، وكل مربع صغير يمثل وحدة مساحة ، وندرس أيضا الأشكال الهندسية وأسمائها مثل المربع والمستطيل والمعين والمسدس وغيرها ،كما في الشكل التالي :

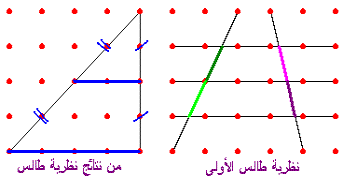
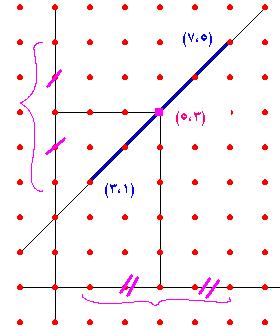
(4)- دراسة مفاهيم التوازي والتعامد والتناظر والدوران كما في الشكل :

(5)- دراسة الزوايا وأنواعها ، الزوايا المتجاورة ، والمتقابلة بالرأس والمتبادلة داخليا .

(6)- نظريتي طالس الأولى والثانية ونتائجهما :

والتي تنص على انه إذا حددت مستقيمات متوازية قطعا متطابقة على قاطع فإنها تحدد قطعا متطابقة على أي قاطع آخر .

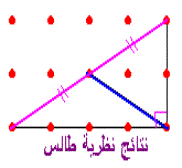
ومن نتائجها أن " طول القطعة المحدودة بمنتصفي ضلعي مثلث تساوي نصف طول الضلع الثالث"

ومن نتائجها انه " في مثلث قائم الزاوية ، طول المتوسط على الوتر يساوي نصف طول الوتر"

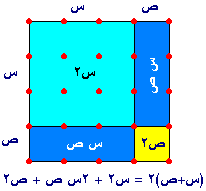
ونظرية طالس الثانية التي تنص على انه " إذا حددت عدة مستقيمات متوازية قطع متناسبة على قاطع فإنها تحدد قطعا متناسبة على أي قاطع آخر"

(7)- تطابق المثلثات وتشابهها ومجموع زوايا المثلث:

(8)- دراسة المتطابقات :

فمثلا المتطابقة (س+ص)² = س² + 2س ص + ص² يمكن فهمها بسهولة من خلال الشكل المقابل

وبنفس الطريقة يمكن رؤية أن

س² - ص² = (س+ص) (س-ص)

(9)- تمثيل الأزواج المرتبة وتمثيل العلاقات الخطية:

برسم محورين متعامدين على اللوحة باستخدام المطاطات تصبح اللوحة شبكة تربيع وبالتالي يمكن تمثيل الأزواج المرتبة عليها ودراسة معادلات الخط المستقيم وتمثيله بيانيا .

ويتضح كيف أن الميل ثابت كما في الشكل 1÷1 أو 2÷2 ، ويبدو كذلك الجزء المقطوع من محور الصادات =2

وبذلك يمكن كتابة معادلة المستقيم على الشكل : ص = س + 2 وبكل وضوح بحيث نرى الميل ونرى الجزء المقطوع

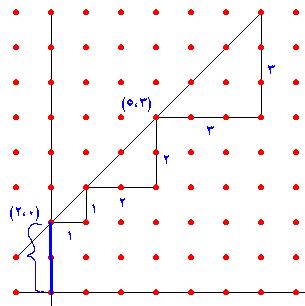
(10)- تحديد منتصف قطعة مستقيمة وطولها :

تتحدد نقطة المنتصف في قطعة مستقيمة بالنقطة التي إحداثياتها هي : نصف مجموع الإحداثيات السينية لطرفي القطعة وَ نصف مجموع الإحداثيات الصادية لطرفي القطعة .

وهذا يبدو واضحا من الشكل لأن طول القطعة المستقيمة كما يظهر في الشكل هو

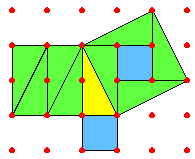
(11)- نظرية فيثاغورس :

تنص نظرية على انه في أي مثلث قائم الزاوية يكون مربع طول الوتر يساوي مجموع مربعي الضلعين الآخرين

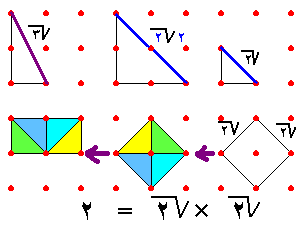
أي أن مساحة المربع المقام على الوتر تساوي مجموع مساحتي المربعين الآخرين المقام كل منهما على ضلع وهذا ما يظهر في الشكل المرافق . والشكل الآخر يبين لنا كيف يبدو العدد جذر 2 أو ضعفه أو مربعه .

(12)- العمليات على الأعداد

مثل عملية الضرب التالية :

(13)- مساحة شبه المنحرف :

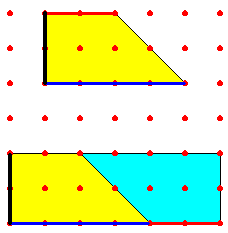
نعتمد في إثبات قانون مساحة شبه المنحرف على تكوين مستطيل باستخدام شبه منحرف آخر مطابق للأصلي فتصبح مساحة شبه المنحرف هي نصف مساحة المستطيل الناتج ،وكما يبدو في الشكل فإن

مساحة شبه المنحرف = نصف مساحة المستطيل

= نصف مجموع القاعدتين × الارتفاع

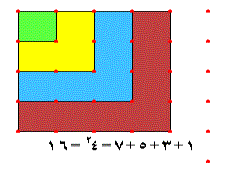
(14) دراسة بعض الأنماط والعلاقات الرياضية :

مثل دراسة مجموع الأعداد الفردية واثبات أن مجموع الأعداد الفردية من 1 ، 3 ، ... إلى العدد الفردي (ن) يساوي ( ن² )