15

      

اضغط هنا لمشاهدة البرمجية

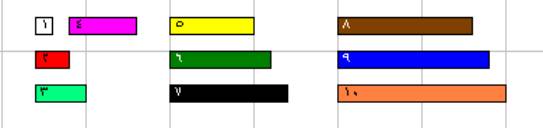
قضبان كوازينير

 قضبان كوازينير وتسمى أحيانا قطع الأعداد الصحيحة تستخدم لدراسة وتقريب العديد من المفاهيم الرياضية والهندسية أحيانا واكثر استخداماتها في المرحلة الابتدائية.

وهذه القضبان ثابتة الدلالة واللون والقيمة حيث أن :

  واجهة العمل :

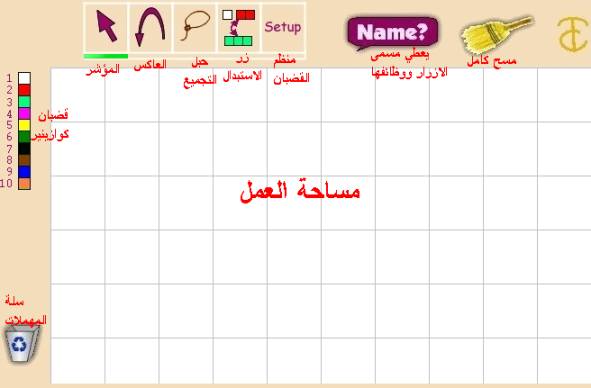
الواجهة واضحة وسهلة جدا كما في الصورة

دعنا الآن نصف الأدوات الأخرى على اليسار و الأعلى وهي تغير العمل كلما ضغطت على زر الفارة ،  ويصف الجدول التّالي كلّ الوظائف المتاحة :

بعض استخدامات قضبان كوازينير :

(1)- عملية التصنيف باللون والشكل :

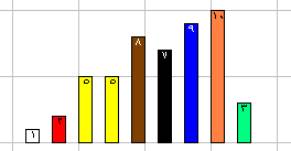
   (2)- مقارنة الأعداد ،والعد والمقارنة والقياس والأعمدة البيانية  :

  (3)-دراسة مكونات العشرة والإبدال :

حيث يجد المتعلم من خلال تعامله مع البرنامج والقضبان أن :

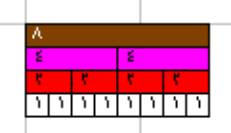
1+9=10     2+8=10     3+7=10 ....       9+1=10 

                                                          

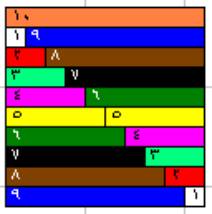
(4) الجمع :

بعد أن يكون المتعلم قد تعلم العلاقة بين القضبان من خلال تعامله معها وطريقة المقايضة ، سوف يجري عملية الجمع بشكل طبيعي ومفهوم كما هو موضح في الشكل التالي :

2+5 = 7 ،   2+2+3 = 7 ،               7+8 = 15

                     

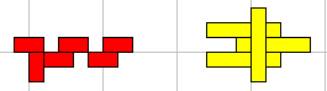
(5)- الطرح :

تقوم فكرة الطرح هنا كما هي عادة على الأخذ حيث نمثل المطروح منه ثم نمثل عليه المطروح فيبقى ناتج الطرح هو العدد المكمل للمطروح منه.

                        

  (6) الضرب

 هنا يتم بالفكرة المعهودة وهي التكرار ( أي تكرار أحد المضروبين بعدد مرات الآخر )

كما نرى في  3 × 4 = 12   أو   2 × 6 = 12  

                                 

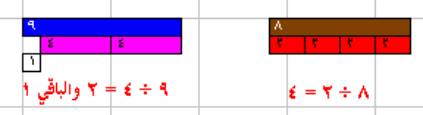
(7) القسمة :

تقوم فكرتها على أساس تمثيل المقسوم ثم محاولة تمثيل قطار من وحدات المقسوم عليه طوله يساوي المقسوم عليه فيكون عدد الوحدات هو الناتج

              

  (8)- الأعداد الزوجية الفردية :

يكون العدد زوجيا إذا استطعنا تمثيله بقطع صحيحة من القطعة رقم 2 ويكون فرديا إذا لم نستطع .

            

   (9)- قواسم العدد والقاسم المشترك الأكبر :

تقوم الفكرة على أساس بناء العدد ثم محاولة بنائه من قطع صحيحة أخرى بكل الطرق الممكنة،

مثل قواسم العدد 8 : 1 ، 2 ، 4 ، 8

وبنفس الطريقة نوجد قواسم أي عدد آخر ونوجد اكبر قاسم مشترك من بين قواسم العددين .

                 

(10)- الأعداد الأولية :

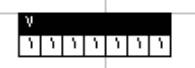
العدد الأولي هنا هو العدد الذي لا يمكن تغطيته إلا بأطوال الوحدة أو الطول نفسه :

مثل العدد 7

                   

  (11)- المضاعفات والمضاعف المشترك الأصغر :

تقوم المضاعفات هنا على فكرة بناء قطار طويل من نفس العدد وحساب طوله

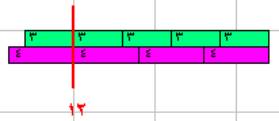
ولإيجاد المضاعف المشترك الأصغر لعددين نبني قطارين معا حتى يتساوى طوليهما

كما في العددين 3 ، 4 حيث مضاعفيهما المشترك الأصغر = 12