القطع الهندسية

للتعرف على كيفية عمل البرمجية أنت بحاجة إلى قراءة الشرح

شرح القطع الهندسية :

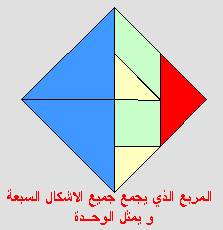
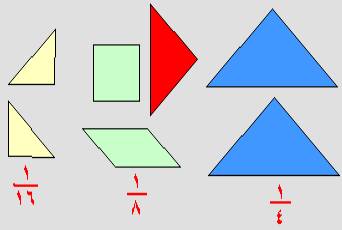
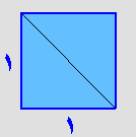
هي عبارة عن سبع قطع منها مثلثان متطابقان كبيران و مثلثان متطابقان صغيران ومثلث وسط بينهما ، ومربع ، ومتوازي أضلاع ، وهذه القطع مصنوعة بشكل مميز بحيث يمكن تركيب أي قطعتين أو ثلاثة منها معا بحافة واحدة منطبقة على الأقل ، وكذلك جميع المثلثات متطابقة الساقين وقائمة الزاوية.

واجهة البرنامج :

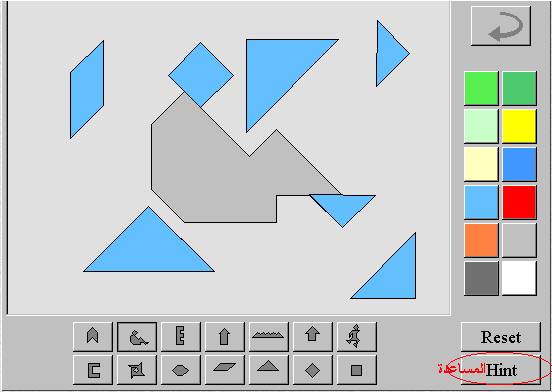
قواعد استخدام البرنامج:

× يتم تحريك الأشكال بالضغط عليها بالفارة وسحبها لإلصاقها بأي شكل آخر .

× يتم تلوين الأشكال بالتأشير عليها بالفارة ثم ضغط اللون المناسب .

× يمكن تكبير واجهة البرنامج لظهور كامل العناصر باستخدام الزر (F11) في أعلى لوحة المفاتيح

× يمكن تدوير أي قطعة بوضع الفارة عند ركن القطعة حيث تظهر نقطة سوداء يمكن من خلالها تدوير القطعة بسحب الفارة في أي اتجاه .

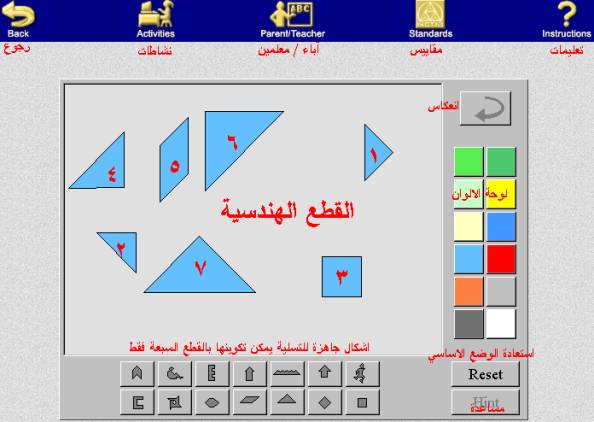
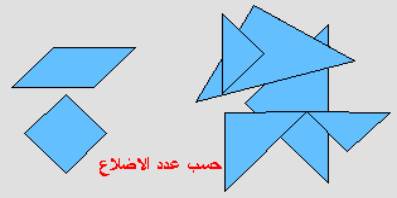
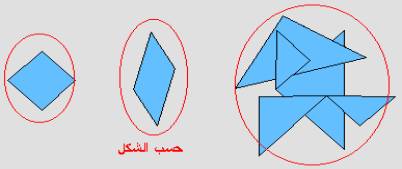
أمثلة لاستخدامات القطع الهندسية من خلال البرنامج :

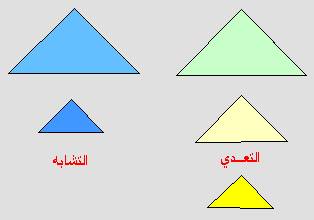
· تعلم مفاهيم التصنيف حسب عدد الأضلاع أو حسب المضلعات المنتظمة أو حسب الزاوية القائمة.

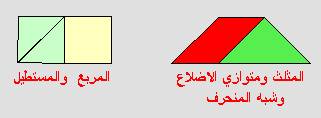
· دراسة الأشكال الهندسية المألوفة : مربع ، مستطيل ، مثلث ، متوازي أضلاع ، شبه منحرف .

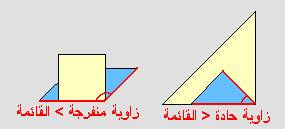
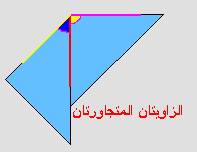
دراسة أنواع الزوايا والمقارنة بينها.

· دراسة العلاقة بين أطوال أضلاع القطع .

· المقارنة من حيث الكبر والمساحة والمحيط ودراسة علاقة التعدي و التشابه .

· مجموع زوايا المثلث والزاوية الخارجية في مثلث

· الزاويتان المتناظرتان والزاويتان المتبادلتان

· الزاويتان المتجاورتان

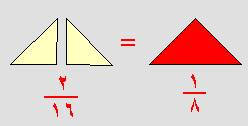
· الكسور والكسور المتكافئة.

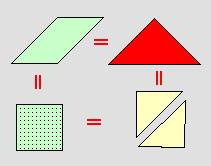
من خلال تركيب أشكال معروفة ( مثلث ، مربع ، مستطيل ) من هذه القطع السبعة أو بعضها يمكن معرفة العلاقات بين الأشكال السبعة ودراستها .

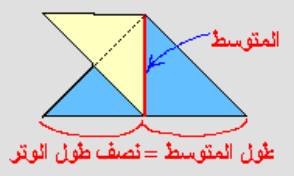
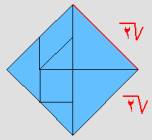
· المستقيم المتوسط في مثلث قائم الزاوية يساوي نصف الوتر

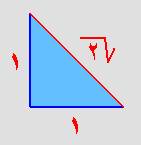
· المستقيم الواصل بين منتصفي ضلعي مثلث يوازي الضلع الثالث ويساوي نصفه .

· نظرية فيثاغورس

تنص نظرية على انه في أي مثلث قائم الزاوية يكون مربع طول الوتر يساوي مجموع مربعي الضلعين الآخرين

أي أن مساحة المربع المقام على الوتر تساوي مجموع مساحتي المربعين الآخرين المقام كل منهما على ضلع وهذا ما يظهر في الشكل المرافق .

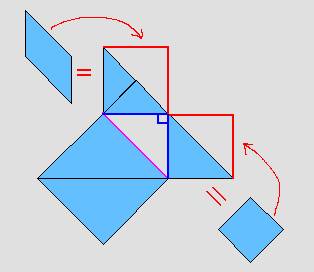
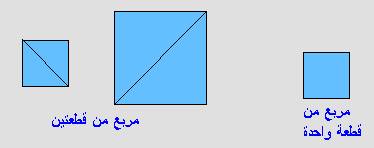
· حاصل ضرب جذر 2 في جذر 2 يساوي 2 .

وهذا الشكل يوضح لنا كيف تكوّن العدد جذر 2 لدينا من خلال القطع .

ولو عدنا للمربع الكبير الذي يتكون من جميع الأشكال السبعة لوجدنا أن المثلثين الكبيرين مساحتهما =1 وهما يساويان نصف الشكل .

وعليه تكون مساحة الشكل كامل = 2 = مساحة المربع الكبير = جذر 2 × جذر 2 .

· يمكن كذلك استخدام هذه القطع للتسلية من خلال البرنامج والذي توجد فيه نماذج جاهزة والمطلوب إعادة تكوين الشكل من خلال هذه القطع ويوجد زر للمساعدة في إظهار بعض الخطوط .

· ويمكن كذلك محاولة تكوين مربع من بعض القطع أو منها كلها كما رأينا في المربع الكبير .

ويمكن بالطبع استنتاج المثلث المكون من هذه القطع من خلال تكوينات المربع السابقة لأنها تحوي غالبا مثلثات .