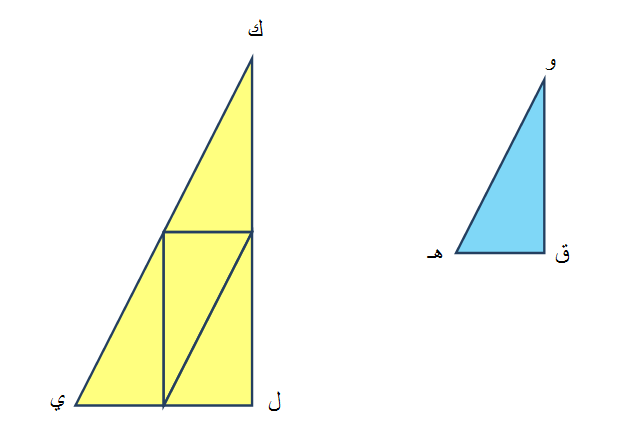
التشابه:
تسمى المثلثات التي لها الشكل نفسه مثلثات متشابهه، إلا أنه ليس من الضروري أن تكون لها أطوال الأضلاع نفسها .
وبإستخدام نماذج المثلثات يستطيع الطالب وبشكل ملموس التعرف على التشابه بين مثلثين قام بتكوينهما أو قدما له لكنه يستطيع التعامل مع اجزاءهما بشكل محسوس.
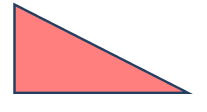
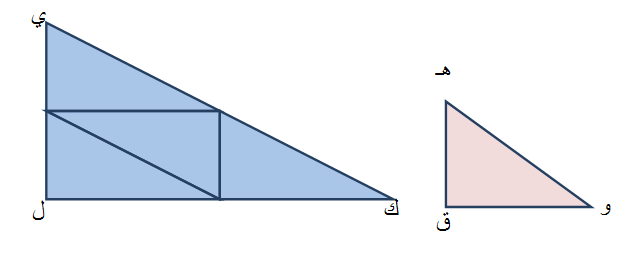
والشكل التالي يوضح الفكرة
يستطيع الطالب أن يستنتج أن الزوايا الثلاث في المثلثين متطابقة .
لانها ببساطه تمثل نفس الزوايا في المثلثين الصغير والمشابه له الكبير . ويستطيع الطالب ان يدرك ذلك بشكل محسوس من خلال تحريك المثلثات ووضعها بعضها فوق بعض ليتاكد من ذلك .
ليستنتج أن : زاوية و تطابق زاوية ك
زاوية هـ تطابق زاوية ي
زاوية ل تطابق الزاوية ق
نسبة التشابه :
النقطة التي يمكن أن يستنتجها الطالب أيضا بطريقة محسوسة هي نسبة التشابهه بين المثلثين. فمن خلال قطع المثلثات المستخدمة يستطيع الطالب أن يقارن بين الأضلاع في المثلثين .
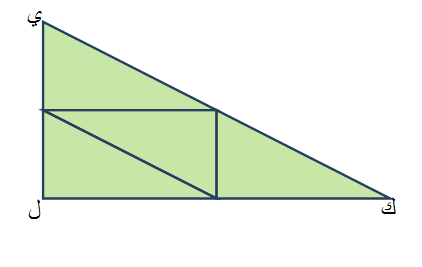
فيجد أن طول الضلع و ق يقابله وحدتين من ذات الضلع في المثلث الكبير والذي يمثله الضلع ك ل .
كما أن الضلع ق هـ يقابله وحدتين من ذات الضلع في الضلع الكبير والذي يمثله الضلع ل ي .
الوتر في المثلث الصغير يقابله أيضا وحدتين من ذات الضلع في المثلث الكبير والذي يمثله الضلع ك ي .
ومن خلال هذه المقارنة بين أطوال أضلاع المثلثين يستنتج الطالب بطريقة محسوسة أن النسبة بين تشابه المثلثين هي 1 : 2 .
علاقة نسبتي مساحتي المثلثين بنسبتي تشابهما :
من خلال عدد المثلثات المستخدمة في عملية تكوّين المثلث الكبير يستطيع الطالب بطريقة محسوسة وسهلة في إيجاد النسبة بين مساحتي المثلثين.
وبالتالي يستنتج الطالب وبكل سهولة أن نسبة بين مساحتي المثلثين هي 1 :4
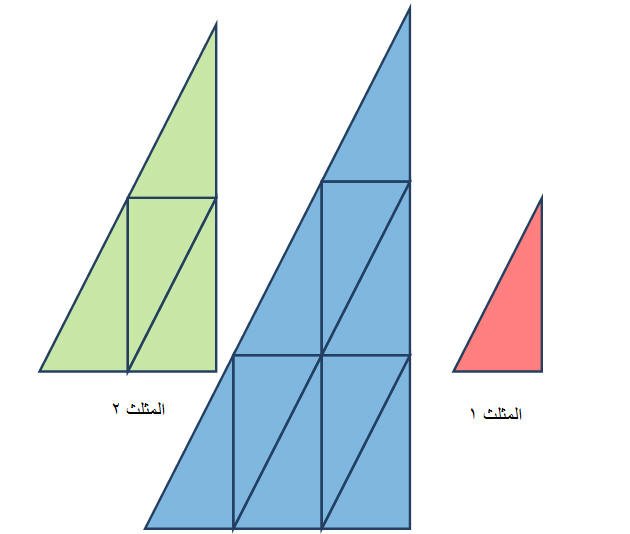
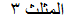
وبملئ الجدول التالي :

يستنتج الطالب :
أن النسبة بين مساحتي مثلثين متشابهين تساوي مربع نسبة التشابهة
علاقة نسبتي محيطي المثلثين بنسبتي تشابهما
 |
 |

وبالتالي فإن النسبة بين محيطي المثلثين = 1: 2
وقد أوجد الطالب في نشاط سابق نسبة التشابه بين المثلثين = 2:1
ومن خلال النشاط السابق يقوم الطالب بملئ الجدول التالي

ليستنتج الطالب :
أن النسبة بين محيطي مثلثين متشابهين تساوي نسبة تشابهما
علاقة إرتفاعي مثلثين متشابهين بنسبتي تشابهما
من خلال معرفة الطالب بأبعاد المثلث المستخدم يستطيع إيجاد ارتفاعه.
فارتفاع المثلث الصغير = 1
محيط المثلث الكبير = 2 .
وبالتالي فإن النسبة بين ارتفاعي المثلثين = 1: 2
وقد أوجد الطالب في نشاط سابق نسبة التشابه بين المثلثين = 2:1
ومن خلال النشاط السابق يقوم الطالب بملئ الجدول التالي :

ليستنتج الطالب :
أن النسبة
بين ارتفاعي مثلثين متشابهين تساوي نسبة تشابهما
تطبيقات :
حدد هل الشكلين التاليين متشابهين ؟ لماذا ؟
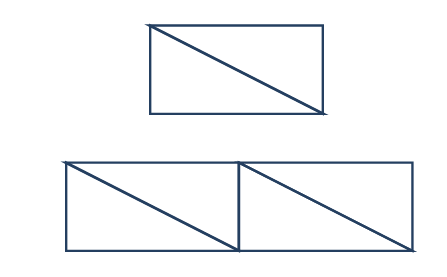
كوّن مستخدما المثلثات القائمة شكلا مشابها للشكل التالي: