نظرية طالس :

 

من الدروس التي يمكن تقديمها بإستخدام المثلثات القائمة إثبات نظرية طالس  " أن المستقيم الواصل بين منتصفي ضلعين في مثلث يوازي الضلع الثالث ويساوي نصف

طوله ".

نستخدم أربعة مثلثات لتكوين مثلث قائم الزواية بحجم كبير  كما هو موضح في الشكل التالي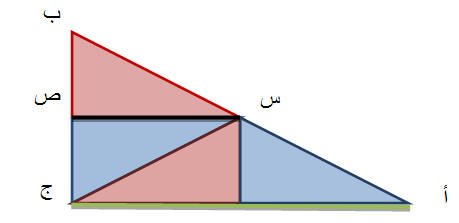

نجد المستقيم باللون الأسود هو مستقيم يصل منتصفي ضلعين كما هو واضح بشكل محسوس للطالب كما أنه يوازي الضلع باللون الأخضر من خلال الزوايا القائمة .

 

من الشكل الذي تم تكوينه يستطيع الطالب أن يستنتج طول  س ص  يساوي نصف طول  أ ب .

 

ونستطيع  أن نبرهنها بطريقة محسوسة

نقوم بأكمال الجزء السفلي بحيث يكون متوازي أضلاع أ س هـ ج كما هو مبين في الشكل التالي

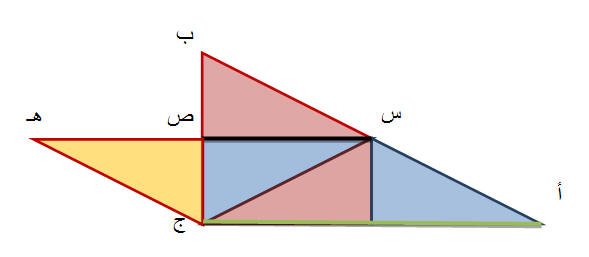
من الشكل يستنتج الطالب بطريقة محسوسة أن المثلثين أ ب ج  و  ص هـ ج متشابهان :

·       قياس زاوية س = قياس زاوية هـ (نفس الزاوية في المثلث ) يمكن إثبات ذلك من خلال كونهما  متبادلتان .

·       قياس زاوية ص 1= قياس زاوية ص 2 (الزاوية القائمة في المثلثين )يمكن إثبات ذلك كونهما متقابلتان بالرأس .

قياس زاوية ج = قياس زاوية ب (نفس الزاوية في المثلث ) يمكن إثبات ذلك من خلال كونهما  متبادلتان