التحويلات الهندسية :
تسمى حركة الشكل الهندسي تحويلا هندسيا ويسمى الشكل الناتج عن هذه الحركة صورة الشكل وأنواع التحويلات الهندسية ( الأنسحاب ، الإنعكاس ،الدوران ) .
الانسحاب:
يعرّف الانسحاب على أنه إزاحة الشكل دون تدويره ولا ينتج عن ذلك تغير في مقاساته أو شكله .
ومن خلال استخدام نماذج المثلثات يستطيع الطالب إجراء العديد من عمليات الإنسحاب ولعدد من الأشكال بطريقة محسوسة لا يكتفى فيها بالرسم فقط .
والشكل التالي يوضح الفكرة
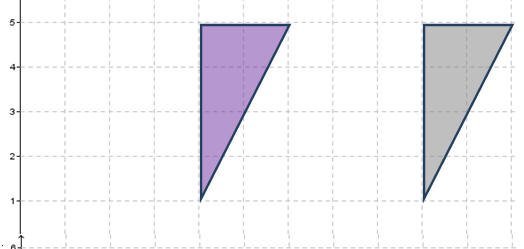
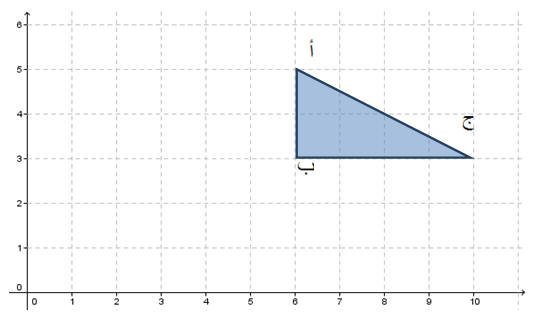
فالمثلث أ ب جـ رؤوسه أ(6،5)،ب(6،3)،جـ(10،3) .وعند إجراء عملية إنسحاب له بمقدار خمس وحدات إلى اليسار تتكون صورة المثلث في الشكل التالي
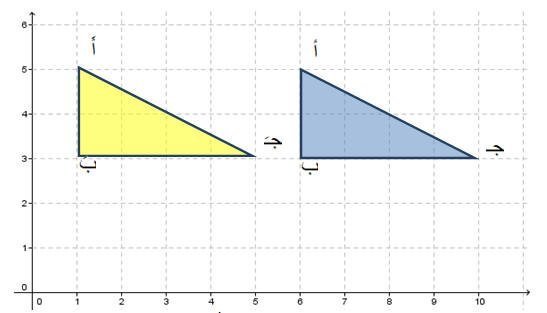
وتصبحالأزوراج المرتبة لرؤوسه الجديدة هي أَ(1،5)،بَ(1،3)،جـَ(5،3) .
هنا يقوم الطالب بعملية الانسحاب بشكل محسوس بحيث يحرك فعليا الشكل المعطى مدركا للاتجاه والمسافة في الوقت ذاته .
ويمكن تكوين العديد من الأشكال بإستخدام نماذج المثلثات ومن ثم إجراء عملية الانسحاب عليها كما هو موضح في المثال التالي
مثال آخر :
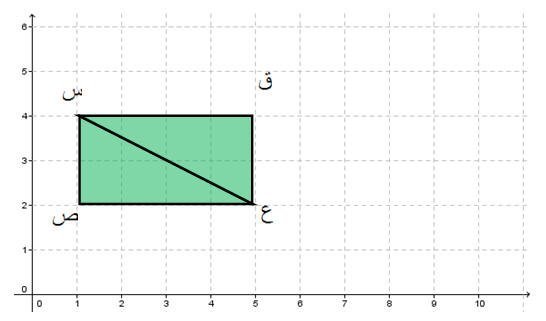

تصبح رؤوس المستطيل الناتج من عملية الانسحاب قَ (4،11) ، سَ (4،7) ،صَ (2،7) ، عَ (2،11) .
ويمكن أن يكون الانسحاب في اتجاهين في الوقت ذاته كما هو موضح في المثال التالي .
مثال آخر:
نفذعملية إنسحاب للشكل التالي وحدتين إلى اليمين ووحدتين إلى الأسفل
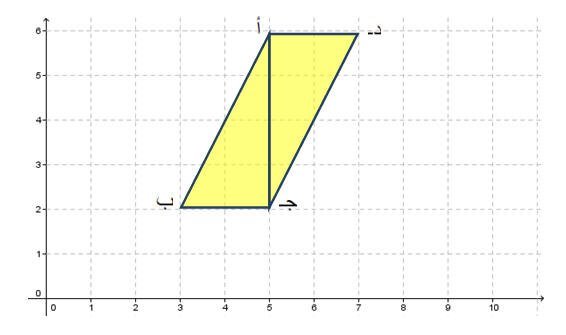
والذي تقع رؤوسه أ (5،6) ، ب (3،2)،جـ (5،2) ،د (7،6)
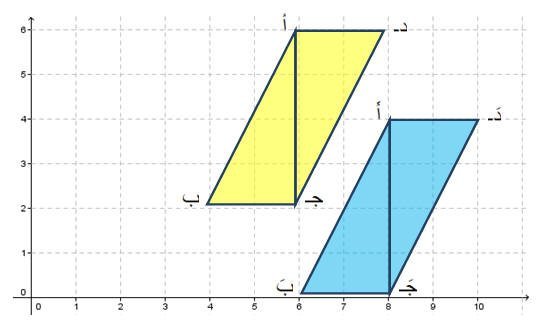
لتصبح صورته بالانسحاب أَ (8،4) ،بَ (0،6)، جـَ (0،8)،دَ (4،10).
الانعكاس:
يعرف الانعكاس على أنه قلب الشكل الهندسي حول مستقيم والحصول على صورة مرآة لهذا الشكل ،ويسمى المستقيم محور الانعكاس .
ومن خلال استخدام نماذج المثلثات يستطيع الطالب اكتساب مفهوم الانعكاس ويمارسه بصورة محسوسة.
والشكل التالي يوضح الفكرة
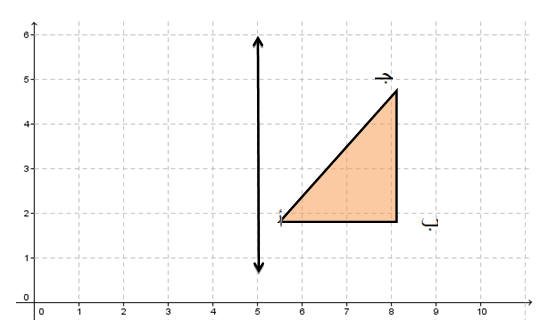
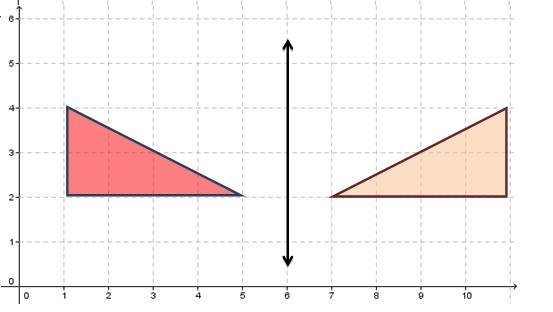
نجد أن صورة المثلث أ ب ج والذي تمثل رؤوسه بالنقاط أ (1،6) ،ب(1،8) ،جـ(5،8) بالانعكاس حول المحور هي المثلث الذي تمثل رؤوسه النقاط أَ (1،4) ،بَ (1،2) ،
جـَ (5،2).
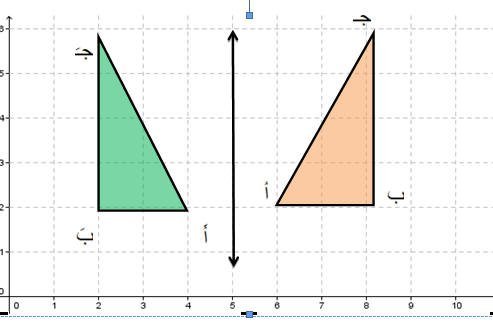
ويستطيع الطالب أن يستنتج أن الرؤوس المتناظرة حول المحور تكون على مسافة متساوية من ذلك المحور
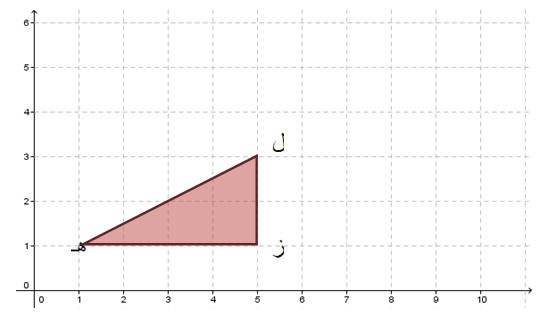
مثال آخر :
أوجد صورة شبه المنحرف التالي بالتناظر حول المحور
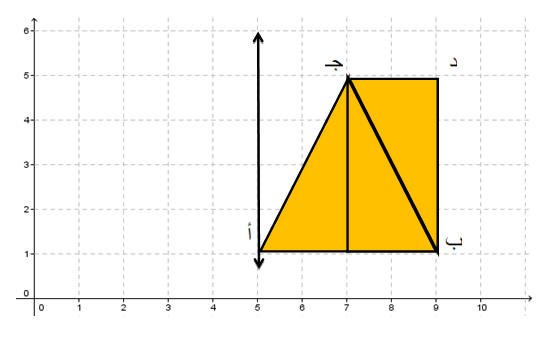
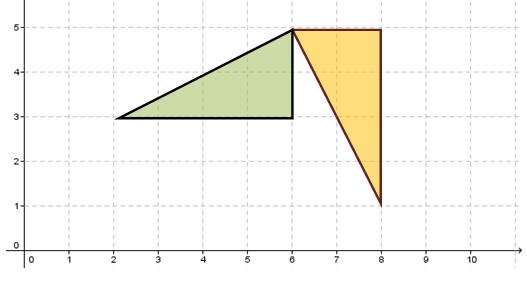
فنجد أن رؤوس شبه المنحرف قائم الزاوية هي أ (1،5) ،ب(1،9) ،جـ (5،7) ، د (5،9) وعند إجراء عملية الانعكاس له بإستخدام المثلثات نجد أن صورته هي
لتمثل رؤوس الصورة المتكونة من عملية الانعكاس أَ (1،5) ،بَ (1،1) ، جـَ (5،3) ،دَ (5،1)
الدوران:
يعرف على أنه تدوير الشكل الهندسي حول نقطة .ويتطلب معرفة مقدار ذلك الدوران وإتجاهه.
ويستطيع الطالب من خلال استخدامه لنماذج المثلثات تنفيذ عملية الدوران بشكل محسوس.
والشكل التالي يوضح الفكرة
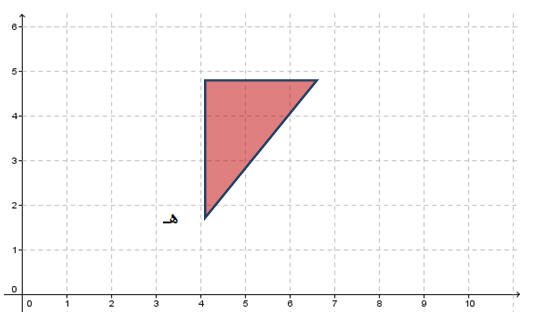
فصورة المثلث السابق بالدوران بإتجاه عقارب الساعه بمقدار 90 ْ حول النقطة هـ
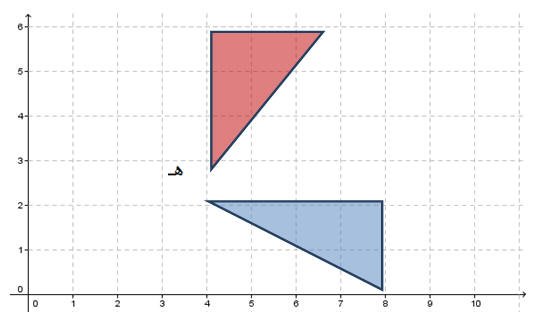
مثال آخر
يستطيع الطالب مستخدما نماذج المثلثات بتدوير المثلث 180 ْ حول النقطة ل والواقعة رؤوسه في المستوى الاحداثي عند النقاط هـ (1،1) ، ز (1،5) ، ل (3،5) وبإتجاه عقارب الساعة ليصبح بالصورة التالية
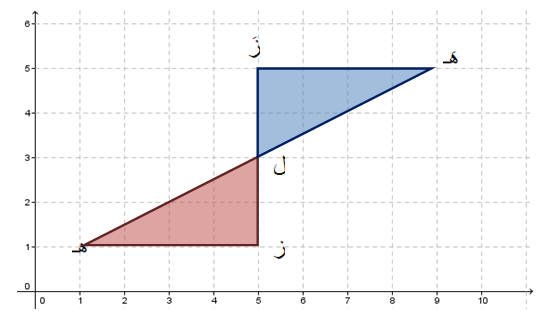
لتصبح صورة المثلث هـ ل ز بالدوران حول النقطة ل 180 ْ هي هـَ (5،9) ،زَ (5،5)، ل (3،5) .
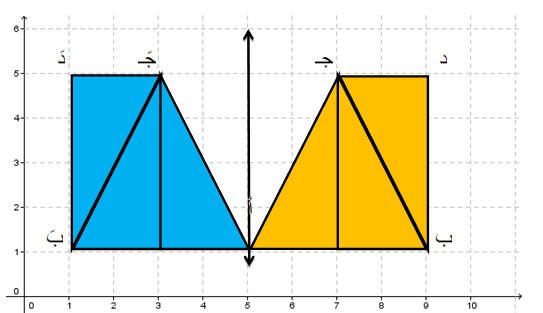
التناظر المركب حول محورين متقاطعين:
يستنتج الطالب أن التناظر حول نقطة هو تركيب تناظرين حول المحور ،بمعنى آخر هو دوران بمقدار 180 ْ حول تلك النقطة . والشكل التي يوضح الفكرة
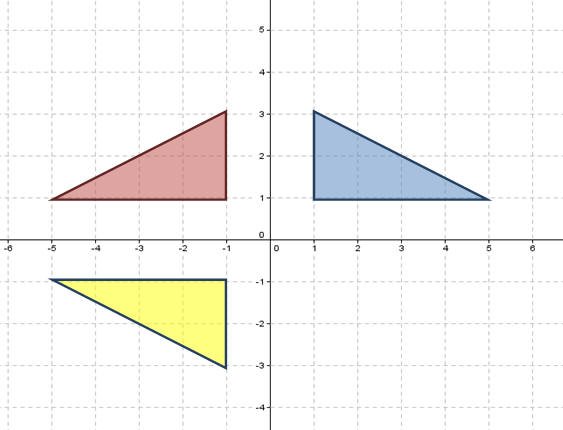
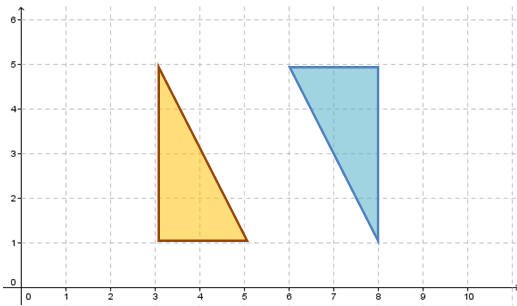
فعلاقة المثلث الأحمر بالأزرق هي صورته بالانعكاس حول المحور السيني ، وعلاقة المثلث الأصفر بالمثلث الأحمر هي صورته بالانعكاس حول محور الصادات.
يترك للطالب استنتاج إجابة السؤال التالي من خلال المثلثات المحسوسة :
ما علاقة المثلث الأصفر بالمثلث الأزرق ؟
الشكل السابق يوضح أن تركيب عملية التناظر حول محورين متقاطعين هو تناظر حول نقطة بدوران مقداره 180 ْ .
وبالتالي فإن
التناظر حول نقطة عبارة عن تركيب تناظرين
التناظر حول نقطة هو دوران بمقدار 180
ويستنتج الطالب أن خصائص التناظر حول نقطة وحول محور والانسحاب هي :
1. يحافظ على الأطوال.
2. يحافظ على الزوايا.
3. يحافظ على التعامد.
التناظر المركب حول محور:
إن استخدام نماذج المثلثات في تكوّين تناظر مركب كول ذات المحور يجعل من عملية استنتاج علاقة الصورة الأخيرة بالشكل الأساسي أمر في غاية السهولة. فعملية إجراء
تناظرين حول ذات المحور ينتج عنه صورة هي ذات الشكل بأبعاده دون تدوير له وهو ما يعرف في التحويلات الهندسية بالانسحاب.
والشكل التالي يوضح الفكرة
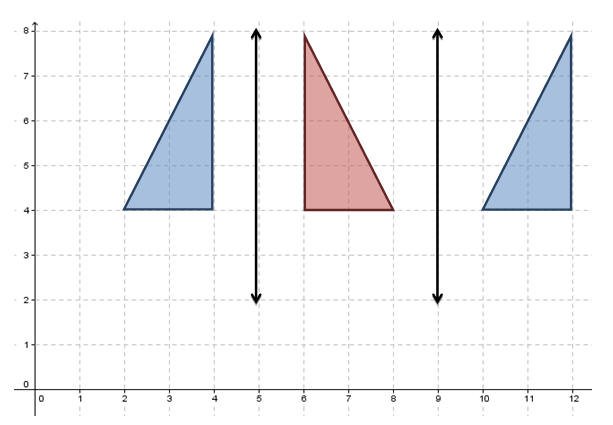
 يستنتج
الطالب وبطريقة ملموسة أن التناظر المركب حول محور هو انسحاب .
يستنتج
الطالب وبطريقة ملموسة أن التناظر المركب حول محور هو انسحاب .
أنشطة : حدد نوع التحويل الهندسي فيما يلي