تكويّن الأشكال :

 

يستطيع المعلم تقديم العدد من الدروس بإستخدامه عدد من المثلثات قائمة الزاوية من خلال تكوين الأشكال والتعرف على خصائصها  كما هو موضح في التالي :

 

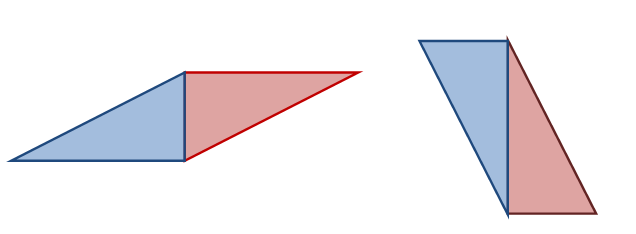
متوازي الأضلاع :

 

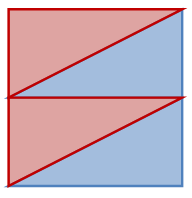
يعرف متوازي الأضلاع بانه شكل رباعي فيه كل ضلعين متقابلين متوازيين. ومن خلال استخدام مثلثين قائمين يستطيع الطالب تكوين متوازي أضلاع ومن ثم يستنتج خواصه كما

 

هو موضح في الشكل التالي:

 

 

 

ويستنتج الطالب أن :

 

·       الأضلاع المتقابلة متطابقة ، فضلعين من اضلاع متوازي الأضلاع عبارة عن الوتر في كل مثلث قائم والضلعين الآخرين عبارة عن أحد أضلاع الزاوية القائمة.

·      

أن الأضلاع المتقابلة متوازية .

 

  

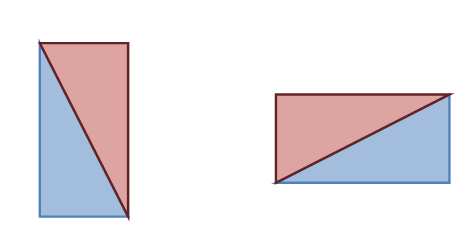
المستطيل :

 

من المعلوم أن المستطيل شكل رباعي فيه كل ضلعين متقابلين متطابقين ومتوازيين وزواياه الأربع قوائم ويستطيع الطالب الوصول إلى هذا التعريف من خلال مثلثين قائميي

 

الزاوية كما هو موضح في الشكل التالي :

 

 

ويستنتج الطالب بطريقة محسوسة أن :

·       أن الأضلاع المتقابلة متطابقة لأنها تمثل نفس الضلع في المثلث الآخر .

·       أن الزوايا الأربع قوائم ،لدينا زاويتين قياسهما 90 ْ وزاويتين عبارة يساوي مجموعهما 90 ْ .

·       أن الأضلاع المتقابلة متوازية .

 

 

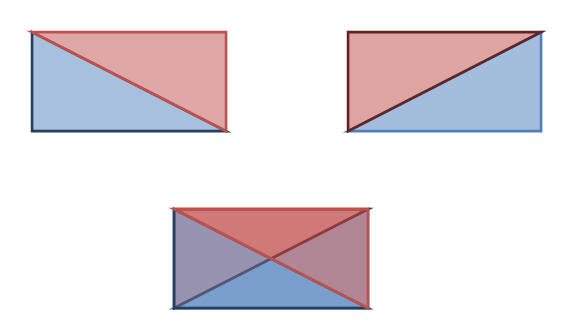
كما يستطيع الطالب استنتاج أن قطري المستطيل متطابقين على اعتبارأن القطر هو الوتر في كل مثلث قائم الزاوية كما يوضح الشكل التالي

 

 

 :

 

 

المعين :

المعين شكل رباعي أضلاعه الأربعة متطابقة وكل ضلعين متقابلين متوازيين. ويستطيع الطالب تكوين المعين مستخدما أربعة مثلثات قائمة كما هو موضح في الشكل التالي :

 

 

 

 

                                             

 

 

ومن خلال النشاط السابق يستنتج الطالب أن :

·       أضلاع المعين الأربعة متطابقة على أعتبار أنها الوتر في كل مثلث.

·       أن كل ضلعين متقابلين متوازيين .

·       كل زاويتين متقابلتين متطابقتين .

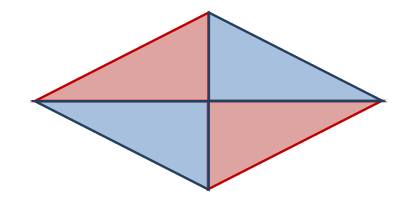
كما يستطيع الطالب استنتاج أن قطرا المعين متعامدين كونهما ضلاعا الزاوية القائمة في كل مثلث.كما هو موضح في الشكل التالي:

 

المربع :

يعرف المربع بأنه شكل رباعي أضلاعه الأربعه متطابقة وزواياه الأربع قوائم . ويستطيع الطالب مستخدما أربعة مثلثات قائمة الزاوية أن يكوّن منها مربعا .كما هو موضح في الشكل التالي:

 

من خلال تكوين الأشكال السابقة يستنتج الطالب أن :

·       الأضلاع المتقابلة متطابقة .

·       أن الأضلاع المتقابلة متوازية .

·       أن الزوايا الأربع قوائم.

 

 

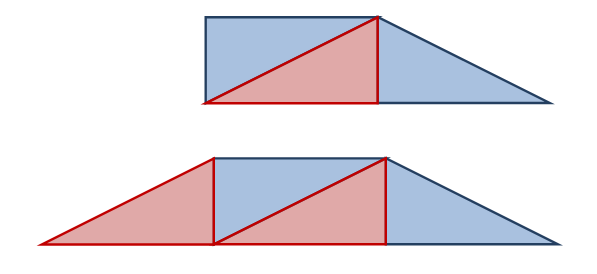
شبه المنحرف : يعرف شبه المنحرف على انه شكل رباعي فيه ضلعان فقط متوازيان وبإستخدام المثلثات يستطيع الطالب أن يكون شبه المنحرف بنوعيه الأول ( القائم الزاوية )

 

والثاني ( متطابق الساقين ) والتعرف على خصائصهما . كما هو موضح في الشكل التالي:

 

ويستنتج الطالب أن :

·       زاويتا القاعدة في شبه المنحرف المتساوي الساقين متساويتان.

·       في شبه المنحرف مجموع قياس يساوي 360ْدرجة .

 

 

المثلث المتطابق الضلعين :

 

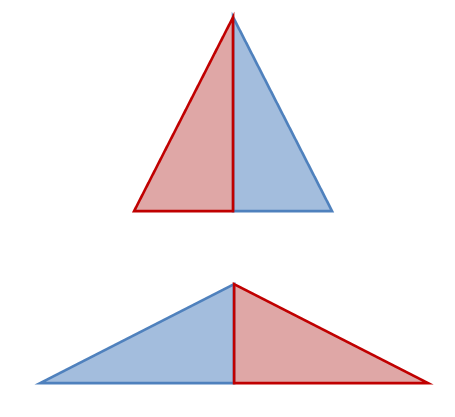
ويُعرّف على انه مثلث فيه ضلعين متطابقين . ومن خلال مثلثين قائمي الزاوية يستطيع الطالب أن يكون مثلثاً متطابق الضلعين.كما هو موضح في الشكل التالي:

 

ويستنتج الطالب عند تكوينه للمثلث المتطابق الضلعين أن:

 

 

 

    

زاويتا القاعدة متطابقتان. حيث تعتبر هي نفس الزاوية في المثلثين قائمي الزاوية .

·       العمود المنصف للضلع الثالث يمر من الزاوية المقابلة له وينصفها.

·       منصف زاوية الرأس هو عمودي على القاعدة ويمر في المنتصف.حيث تكوّن من التقاء ضلع الزاويتين القائمتين للمثلثين قائمي الزاوية.

·       منصف زاوية الرأس هو خط تناظر للمثلث متطابق الضلعين.

 

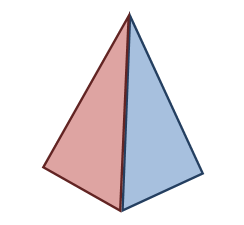
شكل رباعي  :

 

يمكن تكوين شكل رباعي باستخدام مثلثين يكونان زوجين من الاضلاع المتجاورة المتطابقة. كل ضلعين متقابلين فيه ليسا متطابقين ولا متوازين.. كما هو موضح في الشكل التالي:

 

 

 

 

 

 

 

ويستنتج الطالب من خلال الشكل السابق وبطريقة محسوسة أن :

·       هنالك زوجين من الأضلاع المتجاورة المتطابقة .

·       هنالك زوج واحد من الزوايا المتقابلة متطابقة .