المساحة :
بقاء المساحة:
تُعّرف المساحة على أنها عدد الوحدات المربعة التي تغطي سطح شكل ما .
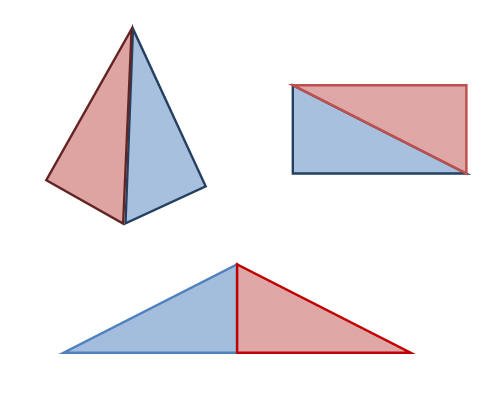
ويستنتج الطالب ومن خلال استخدامه لنفس عدد المثلثات في تكوين أكثر من شكل أن مساحة الأشكال المتكونة هي نفسها كما هو موضح في الشكل التالي :

مثال آخر :
مساحة المستطيل :
تُعرف المساحة بإنها عدد الوحدات المربعة التي تغطي سطح الشكل. وبإمكان الطالب استنتاج مساحة المستطيل بإستخدام الوحدة المربعة حيث يستنتج أن مساحة المستطيل المتكون من مثلثين قائمي الزاوية تساوي وحدتين مربعة كما هو موضح في الشكل التالي
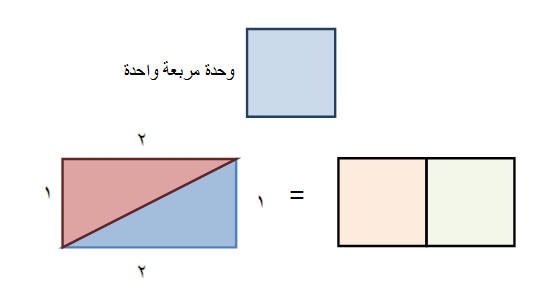
أي أن مساحة المستطيل تساوي وحدتين مربعتين. وتساوي وفق أبعادها 1×2 .
مساحة المستطيل = الطول ×العرض = المساحة بالوحدة المربعة
مساحة المثلث :
من خلال توصل الطالب إلى العلاقة الرياضياتية لمساحة المستطيل يستطيع أن يستنتج مساحة المثلث كما هو موضح في الشكل التالي
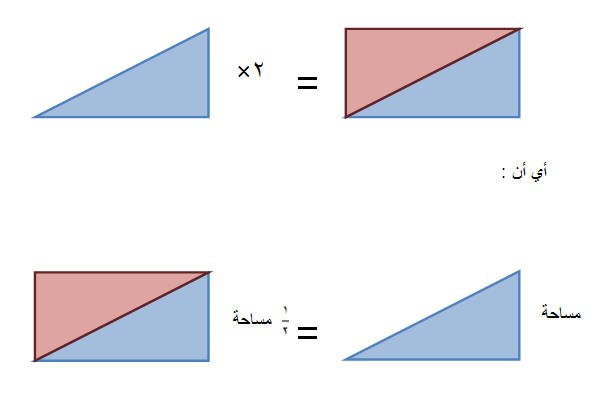
وعليه فإن :
مساحة المثلث = نصف مساحة المستطيل = ½ × 1×2 = 1 وحدة مربعة
½ × (الطول ×العرض)
مساحة المثلث=
½
× القاعدة × الارتفاع = المساحة بالوحدة
المربعة
وهنا يستنتج الطالب بصورة محسوسة سبب وجود ½ في قانون إيجاد مساحة المثلث.
مساحة متوازي الأضلاع :
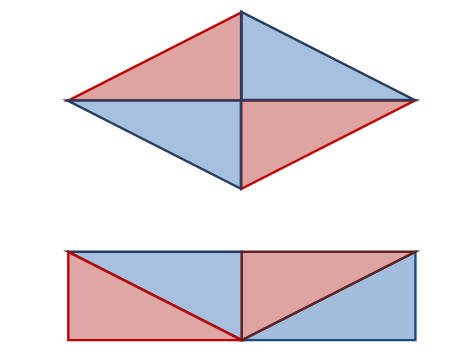
يستنتج الطالب مساحة متوازي الأضلاع عند تكوينه بإستخدام المثلثات قائمة الزاوية ومقارنته بالمستطيل الذي عرف العلاقة الرياضياتية لمساحته. والشكل التالي يوضح ذلك
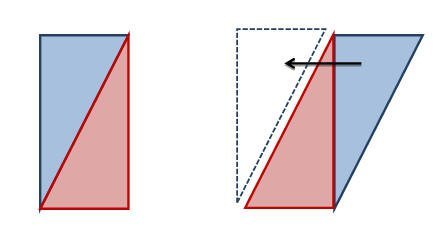
إذن مساحة متوازي الأضلاع = 1×2 = 2 وحدة مربعة
وكعلاقة أو تعميم رياضياتي يمكن صياغتها بالصورة :
مساحة متوازي الأضلاع= القاعدة ×
الارتفاع = المساحة بالوحدة المربعة
مساحة المعين :
بإستخدام المثلثات قائمة الزاوية يسستطيع الطالب التوصل إلى العلاقة الرياضياتية لمساحة المعين كما هو موضح في الشكل التالي:
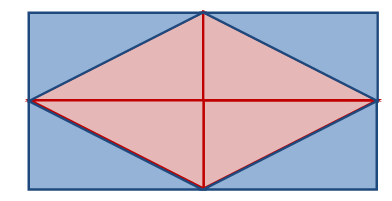
في خطوة سابقة استطاع الطالب أن يستنتج مساحة المستطيل ، وكما هو واضح أن مجموع مساحة المثلثات الداخلية (الحمراء) مساويا لمساحة المثلثات الخارجية (الزرقاء) والتي يعتبر مجموعهما مساحة للمستطيل وبالتالي فإن مساحة المثلثات الحمراء والتي تكوّن معينا مساوية لنصف مساحة المستطيل .ويمكن التعبير عنها كعلاقة رياضياتية بالصورة
مساحة المعين = ½ × حاصل ضرب قطريه = المساحة بالوحدة المربعة
وهنا يستنتج الطالب بصورة محسوسة سبب وجود ½ في قانون إيجاد مساحة المعين.
مساحة المربع :
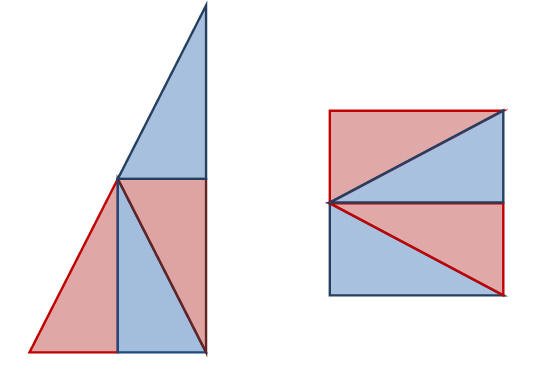
يستطيع الطالب مستعملا أربعة مثلثات تكوين مربعا كما هو موضح في الشكل التالي :
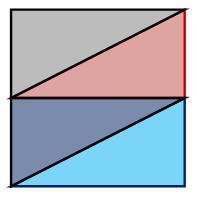
يستنتج الطالب أن المربع حالة خاصة من المستطيل وبطريقة محسوسة أي أن الطول في المربع هو نفس العرض والشكل التالي يوضح الفكرة
وعليه يستنتج الطالب أن :
مساحة المربع = طول الضلع × طول الضلع
توصل الطالب بإستخدام قطع المثلثات إلى مساحة متوازي الإضلاع :
مساحة متوازي الأضلاع = القاعدة
× الارتفاع = المساحة بالوحدة المربعة
ومن خلال تكملة شبه المنحرف بعدد من قطع المثلثات يستطيع الطالب الوصول إلى شكل متوازي الأضلاع زمن ثم مستطيل كما هو موضح في الشكل التالي
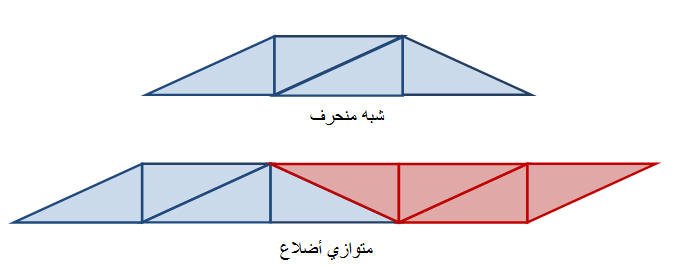
ومن خلال النشاط السابق إستطاع الطالب تكوين متوازي أضلاع مستخدما ضعف العدد من المثلثات التي استخدما في تكوين شبه المنحرف . أي أنه أصبح لدينا شبهي منحرف متطابقين. وبالتالي فإن مساحة شبه المنحرف تساوي نصف مساحة متوازي الأضلاع الذي تمثل قاعدته طول قاعدتي شبه المنحرف الكبرى والصغرى ويتساوى معه في الارتفاع أي :
مساحة شبه المنحرف = ½ ( مجموع طولا قاعدتيه × الارتفاع )
مساحة الأشكال المركبة :
يتكون الشكل المركب من شكلين بسيطين أو أكثر . ويعد استخدام المثلثات القائمة في تقديم هذا الدرس عاملا مساعدا في جعله مفهوم الشكل المركب محسوسا من خلال قدرة الطالب على تقسيمه إلى أشكال يسهل إيجاد مساحتها ومن ثم إيجاد المساحة الكلية لذلك الشكل بجمع المساحات للأشكال المكونة له.
والشكل التالي يوضح الفكرة :
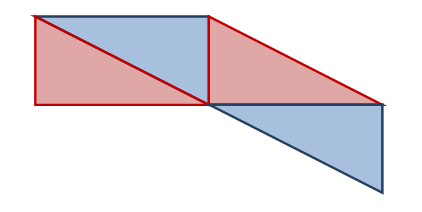
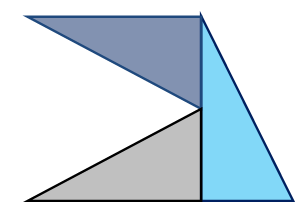
واعتمادا على قدرة الطالب في تحريك المثلثات والتحكم في موقعها يدرك وبشكل محسوس أن الشكل السابق يمكن تقسيمه إلى شكلين يسهل إيجاد مساحتيهما كما هو موضح في الشكل التالي:
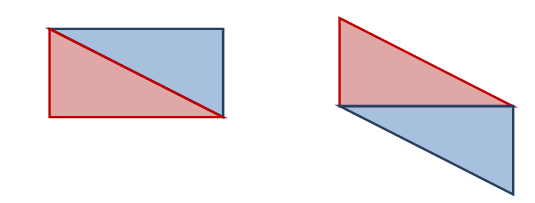
مساحة المستطيل = الطول × العرض= 1×2=2
مساحة متوازي الأضلاع = القاعدة ×الإرتفاع = 2×1=2
مساحة الشكل الكلي = 2+2=4 وحدات مربعةمثال آخر :
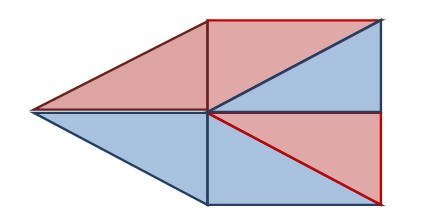
وفي هذا المثال يستطيع الطالب تقسيم الشكل السابق إلى مربع ومثلث متطابق الضلعين أو إلى مستطيلين ومثلثين قائمي الزاوية ومن ثم إيجاد مساحة كل جزء على حده وفي الخطوة الأخيرة يقوم بتجميع مساحات تلك الأجزء ليتحصل على المجموع الكلي لمساحة الشكل المعطى.
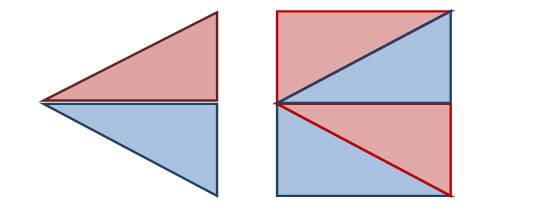
نجد أن مساحة المربع تساوي طول الضلع × نفسه = 2×2=4
ونجد أن مساحة المثلث = ½ القاعدة × الإرتفاع = ½ ×2×2= 2
وبالتالي فإن مساحة الشكل الكلي تساوي مساحة الأجزاء المتكون منها وتساوي مساحة المربع إضافة إلى مساحة المثلث = 4+2=6 وحدة مربعة
مثال آخر :
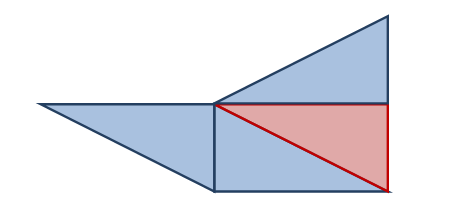
من خلال قدرة الطالب على التعامل مع المثلثات وتحريكها يستطيع أن يقسم الشكل السابق إلى ثلاثة أجزاء مستطيل ومثلثين كما هو موضح في الشكل التالي
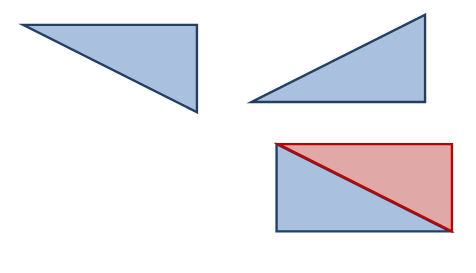
وبالتالي يمكن حساب مساحتها :
مساحة المستطيل = الطول × العرض= 1×2=2
مساحة المثلث = ½ القاعدة × الإرتفاع = ½ ×1×2= 1
المساحة الكلية للشكل = 2+1+1=4 وحدات مربعة