الأشكال ثلاثية الأبعاد :
الشكل ثنائي الأبعاد له طول وعرض أما الشكل الثلاثي الأبعاد فله طول وعرض وإرتقاع والشكل ثلاثي الأبعاد الذي تشكل وجوهه مضلعات يسمى متعدد السط
ومن الدات المرتبطة بالمجسمات لوجه : سطح مستو.
الحرف: المستقيم الناتج عن تقاطع مستويين.
ونمنالدروس التي يمكن أن تقدم بإستخدام نماذج المثلثات قائمة الزاوية بحيث يتعرالطالب عليها وعلى خصائصها بطريقة ملموسة. فوجود البعد الثالث يفرض استخدام المحسوسات في تقديم هذا النوع من الدروس.
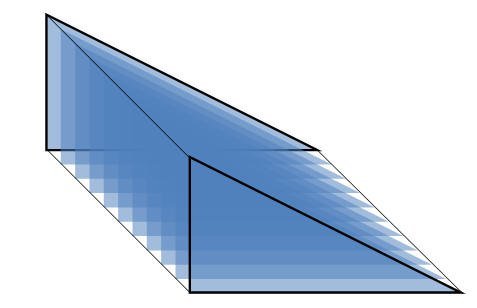
المنشور "الموشور" الثلاثي :
ويعرف بأنه مجسم له وجهان متوازيان ومتطابقان يسميان القاعدتين
نستطيع من خلال استخدام عدد من المثلثات بناء منشور ثلاثي وذلك بوضع عدد من المثلثات بعضها فوق بعض كما هو موضح في الشكل السابق ويستطيع الطالب في هذه الحالة التعامل مع المنشور بشكل ملموس بحيث يتعرف على خصائصه .فمن خلال تحريك المجسم (قلبه) يدرك أن له قاعدتين مثلثتين ، كما يستطيع أن يحدد يحدد أن له خمسة اوجه وتسعة احرف وستة رؤوس.
المنشور "الموشور" الرباعي :
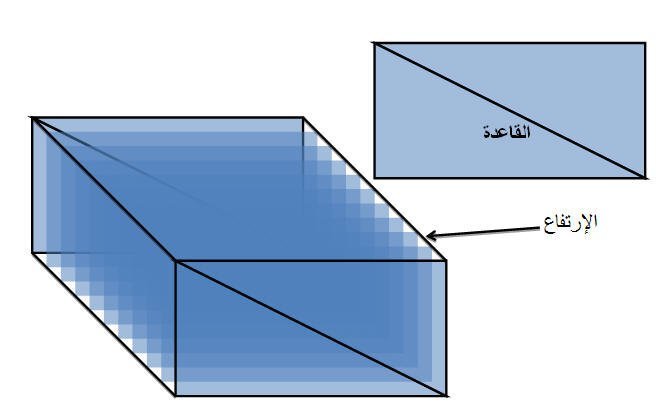
أيضا نستطيع أن نقدم الموشور الرباعي والذي يمكن تكوّين قاعدة الموشور الرباعي بإستخدام المثلثات القائمة من خلال وضع مثلثين بطريقة متلاصقة بوتريهما كما هو موضح في الشكل ومن ثم تكرير الشكل الناتج لنتحصل على موشور رباعي والشكل التالي يوضح الفكرة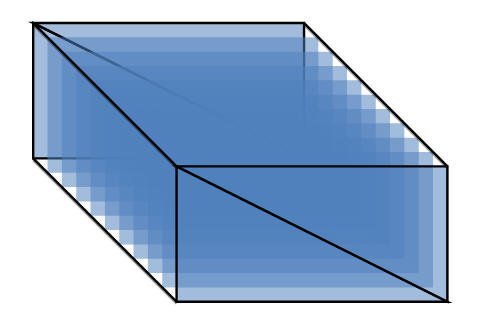
يدرك الطالب بشكل ملموس أن للموشور الرباعي قاعدتين مربعتين وستة أوجه وثمانية رؤوس وإثنا عشر حرفا .
حجم المنشور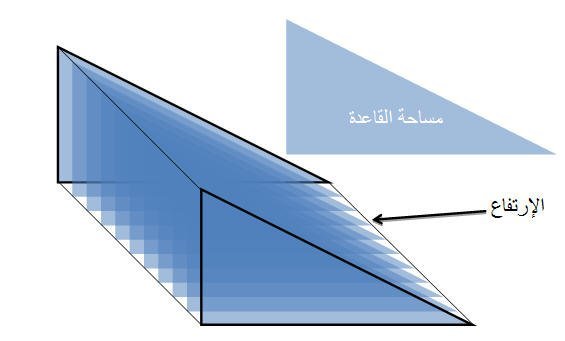
من خلال التعامل مع عدد من المثلثات المكونة للمنشور يدرك الطالب بطريقة ملموسة أن قاعدة المنشور الثلاثي عبارة عن مثلث كما أن الإرتفاع من السهل إيجادة (على اعتبار أن كل القطع ذات سمك ثابت وبالتالي فضرب عددها في ذلك السمك سنتحصل على إرتفاع المنشور ) .
بالمثل نجد أن قاعدة الموشور الرباعي عبارة عن مستطيل متكرر وبالتالي كما أن الإرتفاع من السهل إيجادة (على اعتبار أن كل القطع ذات سمك ثابت وبالتالي فضرب عددها في ذلك السمك سنتحصل على إرتفاع المنشور ) .
وبالتالي فإن إيجاد حجم المنشورتم بطريقة ليست مجردة بل محسوسة ومن ثم يعوض الطالب في العلاقة الرياضياتية لحجم المنشور
حجم المنشور = مساحة القاعدة ×الإرتفاع