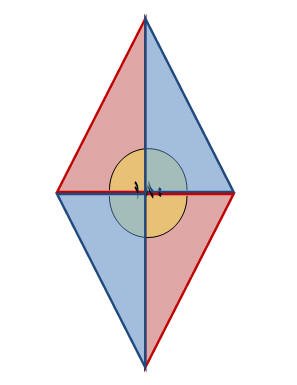
الزوايا :

تعرف الزاوية على أنها شكل يتكون من نصفي مستقيمين لهما نقطة البداية نفسها وتقاس بالدراجات.

 

أنواع الزوايا :

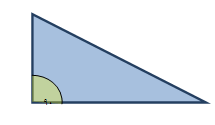
الزاوية القائمة  : وهي الزاوية التي يكون قياسها 90  ْ .

 

ويمكن تمثيلها بإستخدام قطع المثلثات كما هو موضح في الشكل التالي

 

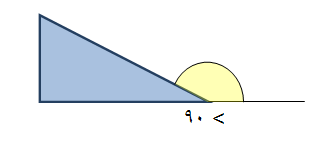
الزاوية المنفرجة : وهي الزاوية التي يكون قياسها أكبر من 90 ْ وأقل من 180 ْ.

 

والشكل التالي يوضح الزاوية المنفرجة .

V

الزاوية الحادة : وهي الزاوية التي يكون قياسها أكبر من 0ْ وأقل من 90 ْ.

 

والشكل التالي يوضح الزاوية الحادة .

 

 

 

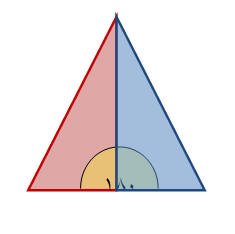
الزاوية المستقيمة: وهي الزاوية التي يكون قياسها مساويا لـ 180  ْ.

 

والشكل التالي يوضح الزاوية المستقيمة حيث يمثل اتحاد الزاويتين القائمتين زاوية مستقيمه قياسها 180  ْ .

 

الزاوية الدائرية: وهي الزاوية التي يكون قياسها مساويا لـ 360  ْ. والشكل التالي يوضح الزاوية الدائرية حيث يمثل إتحاد أربع زوايا قائمة في أربعة مثلثات لتكون

 زاوية دائرية

 

الزوايا المتجاورة  

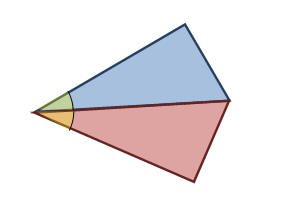
يستطيع الطالب من خلال استخدام نماذج المثلثات أن يمثل زوايا متجاورة وسوف يلاحظ أنه لكي يكوّن زاويتين متجاورتين لابد أن تتوافر فيها الشروط التالية :

1.  أن يكون لهما رأس مشترك.ممثل من أتحاد رأسي المثلث المستخدم .

2.  أن يكون لهما ضلع مشترك . عبارة عن ضلعي المثلثين

3.  أن تكون على جانبي الضلع المشترك.

وفي الشكل السابق الذي تم تكوينه يوجد لدينا زاويتين متجاورتين  الأولى تكونت من إتحاد راسي المثلثتين والثانية تكونت من إتحاد الززاويتين المقابلتين للزاوية القائمة

مثال آخر :

يستطيع الطالب من الشكل السابق أن يحدد الزوايا المتجاورة في الشكل السابق

 

·       الزاوية الأولى نشأت من اتحاد زاويتي الرأس في المثلثين .

·       الزاوية الثانية نشأت من إتحاد الزاويتين القائمتين لتكونا زاوية مستقيمة .

مثال آخر :

من الشكل السابق يستنتج الطالب الزوايا المتجاورة والتي تمثل إتحاد رأس المثلث

 

مع الزاوية المقابلة للزاوية القائمة كما يستطيع أن يحدد أن قياسها مساو لـ 90  ْ .

 

الزوايا المتقابلة بالرأس :

 

تساعد قطع النماذج الطالب على التعرف على هذا النوع من الزوايا والذي سيلاحظ في هذه النوع من الزوايا أن الزوايا أنه يشترط :

1.  أن تكون مشتركة أيضاً في رأس واحد .

2.  أن تكون أضلاعها على الامتداد نفسه .

والشكل التالي يوضح كيفية تكوينها بإستخدام نماذج المثلثات

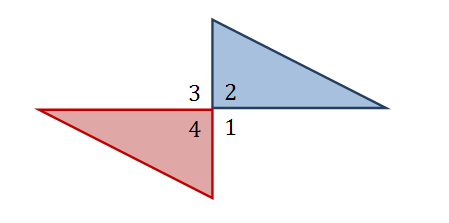
ومن خلال معرفة الطالب بأن المثلثين متطابقين يستطيع أن يستنتج أن قياسهما هو القياس نفسه كما هو واضح في الشكل السابق ويساوي 90 ْ .

 

النقطة المهمة هو القدرة على برهنة ذلك بشكل محسوس كما هو تبعا للخطوات التالية :

 

زاوية 1 + زاوية 2 = 180 ْ  (زاوية مستقيمة )

 

زاوية 3 + زاوية 4 =180 ْ  (زاوية مستقيمة )

 

وبالمقارنة بينهما نستنتج أن :

زاوية 2 = زاوية 4

وبالتالي فإن :

 

كل قطاعين زاويين متقابلين بالرأس متطابقين

 

مثال آخر :

هل نستطيع أن نكوّن زوايا متقابلة بالرأس بإستخدام تلك المثلثات ؟

 

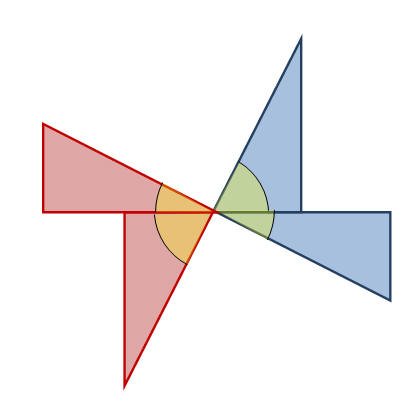
الزوايا المتتامه :

 

من الممكن أن يقدم مفهوم التتام في الزوايا من خلال استخدام نماذج المثلثات قائمة الزاوية  والتي حتما سيكون مجموعي الزاويتين الآخريين في ذات المثلث مساويا للـ 90 ْ .

 

وبالتالي فإن وضع المثلثات بالصورة الواردة أدنا في الشكل يقدم مفهوم التتام وبإمكان الطالب التأكد من مجموعي الزاويتين المتتامتين من خلال وضع الزاوية القائمة في مثلث

 

ثالث على تلك الزاويتين ليتأكد بشكل محسوس أن قياسهما هو 90 ْ .

 

في هذه الحالة نقول أن الزاويتين متتامتان ونقول أيضاً إن الزاوية الأولى هي متممة الزاوية الثانية، وإن الزاوية الثانية هي متممة الزاوية الأولى .

 

 

الزاويتان المتتامتان هما الزاويتان اللتان مجموع قياسهما 90

والشكل التالي يوضح الفكرة

 

الزوايتا ن المتكاملتان :

 

يستطيع الطالب من خلال وضع مثلثين بشكل متجاور بحيث تكون فيه الزاويتان القائمتان متجاورتان لتصنع زاوية مستقيمة أن يتعرف على مفهوم جديد في الزوايا هو التكامل .

 

في هذه الحال نقول : إن الزاويتين متكاملتان ونقول أيضاً إن الزاوية الأولى مكملة الزاوية الثانية أو الزاوية الثانية مكملة الزاوية الأولى

 

والشكل التالي يوضح الفكرة

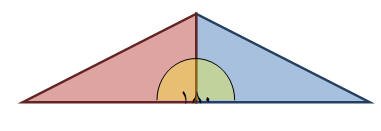
وبالتالي فإن

 

الزاويتان المتكاملتان  هما الزاويتان اللتان مجموع قياسهما مساو لقياس الزاوية المستقيمة 180

 

الزوايا بين متوازيين وقاطع:

 

يستطيع الطالب وبطريقة ملموسة التعرف على عدد من الزوايا الناتجة عن وضع نماذج المثلثات بين مستقيمين متواوزيين وآخر قاطع لهما كما هو مبين في الشكل التالي :

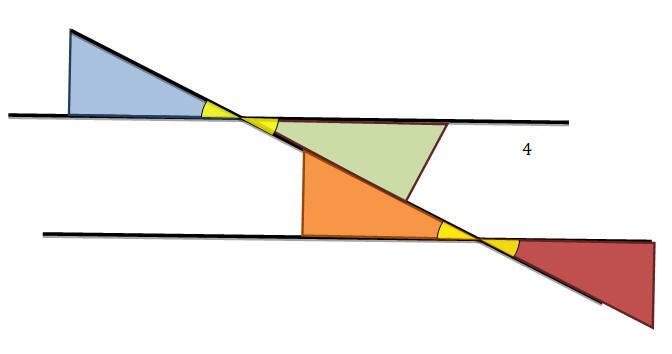
الزوايا المتناظرة : تسمى الزوايا 1 ، 4 زاويتان متناظرتان وتسمى الزاويتان 2،3 زاويتان متناظرتان .

الزوايا المتبادلة: تسمى الزاويتين 1 ،2 والزاويتين 2،4 والزاويتين 3،1 زاويتين متبادلتين.

يستطيع الطالب وبشكل ملموس أن يجيب على السؤال التالي :

·       ما علاقة الزوايا المتناظرة ببعضها ؟

·       ما علاقة الزوايا المتبادلة ببعضها؟

من خلال الشكل الذي قام بتكوينه مستخدما المثلثات يستنتج الطالب أن :

الزوايا المتناظرة متطابقة

الزوايا المتبادلة متطابقة

 

 

 

 

 

 

 

 

 

 

 

 

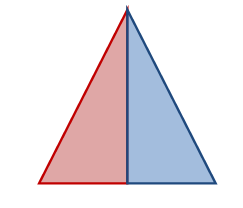
مجموع زوايا المثلث :

 

من خلال قطع المثلثات المستخدمة يستطيع الطالب أن يميّز أن هنالك ثلاث زوايا في كل مثلث . ومن خلال وضع تلك الزوايا جنب إلى جنب يستطيع أن يتوصل وبطريقة محسوسة

إلى قياس تلك الزوايا مجتمعه .

والشكل التالي يوضح الفكرة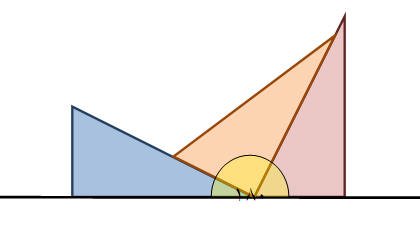

يتضح من الشكل السابق أن زوايا المثلث مجتمعة تكوّن زاوية مستقيمة وبالتالي فإن مجموع قياس زوايا المثلث الداخلية يساوي 180 ْ .

 

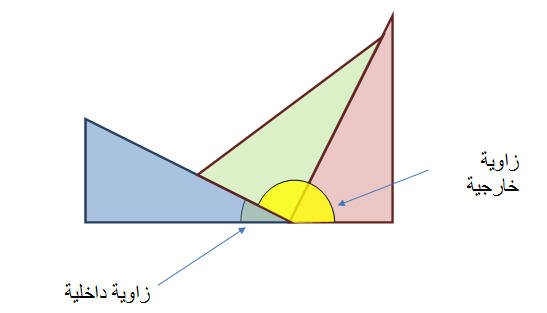
الزوايا الخارجية في المثلث :

 

في البدء يجب ان يتعرف الطالب على مفهوم الزاوية الخارجية في المثلث وهي زاوية تقع خارج المثلث و هي زاوية أحد أضلاعها هو ضلع المثلث ولكن الضلع الثاني لها هو

 

امتداد لضلع المثلث الآخر. 

 

ومن خلال طرح السؤال التالي:

 

هل هنالك علاقة بين الزاوية الخارجية و الزاويتين غير المجاورتين ؟

 

من خلال نماذج المثلثات الموجوده لدى الطالب يستنتج أن قياس الزاوية الخارجية يساوي قياس الزاويتين الداخليتين الغير مجاورتين لها.

والشكل التالي يوضح الفكرة :

وبالتالي فإن

قياس زاوية القطاع الخارجي في مثلث تساوي مجموع قياس زاويتي القطاع الداخلي غير المجاورة لها .