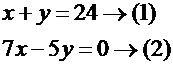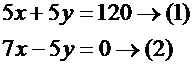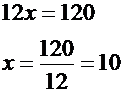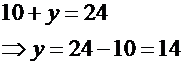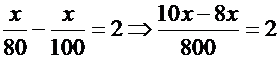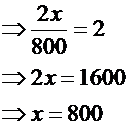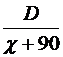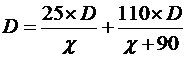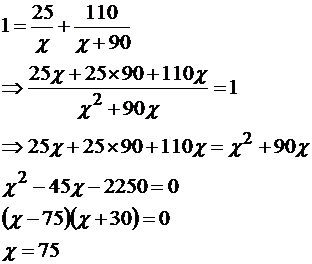|
أمثلة شاملة على استراتيجيات حل المشكلات
أمثلة شاملة : في هذا الباب نستعرض مجموعة من الأمثلة العامة التي يمكن حلها باستخدام أحد الاستراتيجيات السابقة، أو باستخدام أكثر من استراتيجية. وقبل استعراض هذه الأمثلة لابد من التنبيه على عدد من النقاط ، هي : (1) من أهم العوامل التي تساعد في سرعة حل الطالب لمشكلة ما ، هي : مهارة الطالب ، ومستوى ذكائه ، ومعرفته المسبقة بالمعلومات الرياضية. (2) كلما ارتفعت درجة صعوبة المشكلة المعروضة كلما زادت الحاجة لاستخدام أكثر من استراتيجية في حلها . (3) ليس المهم أن يستطيع الطالب حل مشكلة ما باستخدام أحد الاستراتيجيات بعد أن يتدرب على تلك الاستراتيجية مباشرة، وإنما الأهم أن يمتلك الطالب مهارة تحديد الاستراتيجية المناسبة لحل أي مشكلة تعرض عليه. ولاشك أن هذه المهارة لا تأتي إلا بعد طول الممارسة والتكرار في التدرب على هذه الاستراتيجيات، ولكن من الممكن أن نقدم مفاتيح للحل يمكن للتلميذ أن يستأنس بها في اختيار الاستراتيجية المناسبة للحل ، والتي تتمثل في الأفكار التالية:
نستخدم استراتيجية بناء جملة رياضية عندما: · نستطيع أن نجد علاقة تربط بين متغيرات المشكلة، وكانت الجملة الرياضية المكونة تناسب مستوى التلميذ.
ونستخدم استراتيجية المحاولة الخطأ عندما: · تتطلب المشكلة اختيار حل وحيد من مجموعة كثيرة من الحلول الممكنة. · تحوي المشكلة أعداداً كثيرة أو بيانات كثيرة . كما نستخدم استراتيجية البحث عن نمط عندما: · يكون المطلوب هو حل عام للمشكلة ( قانون عام ) ، وبدراسة حالات خاصة منها يمكن أن تكون مفتاحاً لاكتشاف الحل ( النمط ) ، وهي أفضل أنواع الاستراتيجيات في مسائل المتتابعات والمتسلسلات.
بينما نستخدم استراتيجية تبسيط المشكلة في عدد من الحالات: · فعندما تكمن صعوبة المسألة في أرقامها المعقدة ، فإننا نبسط الأرقام المتضمنة في المشكلة من كبيرة إلى صغيرة ، أو من معقدة إلى بسيطة . · وعندما تكون المشكلة مركبة من مشكلات جزئية يمكن تجزئتها عن بعضها فإننا نجزيء المشكلة إلى مشكلات جزئية ونبحث عن حلول جزئية ، وبطريقة ما نتمكن من تركيب هذه الحلول الجزئية لتكون الحل العام للمشكلة الأصلية . · أما إذا كانت شروط المشكلة كثيرة فعندئذ يمكن أن نستخدم طريقة تثبيت أو إضعاف أو حذف بعض الشروط أو تقليل عدد المتغيرات إن أمكن ذلك ، ويمكن التعبير عن ذلك بعبارة بوليا : خذ شرطاً واحداً ثم أضف شرطاً آخر . وفكرة حل المشكلة الجديدة يمكن أن تقودنا إلى الحل النهائي للمشكلة الأصلية . · وإذا كانت فكرة المشكلة مشابهة لفكرة مشكلة أخرى نعرف طريقة حلها، فإننا نقوم بحل المشكلة الجديدة بطريقة مشابهة لحل المشكلة الأولى. · وعندما يكون هناك تماثل في المشكلة فيمكن حلها عن طريق الاستفادة من التماثل الداخلي في بنية المشكلة .
ونستخدم استراتيجية البدء من الخلف عندما : · عندما تتضمن المشكلة سلسلة من الحسابات المتتالية لعدد ما ويعطى الناتج النهائي لهذه الحسابات ، ويكون المطلوب إيجاد قيمة عدد في أحد الحسابات التي في بداية المشكلة والتي قد يصعب حسابها إذا سرنا من المعطيات . وعادة يواجه التلميذ - في هذا النوع من المشكلات - صعوبة في تكوين المعادلات الجبرية أو في استخدام استراتيجيات العمل للأمام بشكل عام .
وأخيراً نستخدم استراتيجية التفكير الإبداعي عندما : · تعجز باقي الاستراتيجيات عن حل المشكلة ، وأحيانا قد تكون أحد الحلول التي تفكر فيها في حل مشكلة ما رغم إمكانية حلها بطريقة أخرى.
مثال (1) : نظم الدوري العام لكرة القدم مباريات بين 10 فرق ، بحيث يلعب كل فريق مع كل فريق آخر مرة واحدة فقط ، كم عدد المباريات التي ستلعبها جميع الفرق ؟ وإذا كانت المباريات ستقام في يوم الخميس فقط ؛ فكم أسبوعاً يلزم لإنهاء الدوري ؟ الحل : أولاً : لفهم المشكلة : استخدم التلاميذ مجموعة من الاستراتيجيات المساعدة : · فمنهم من مثلها تمثيلاً حسياً فاستخدم أقلام ملونة مثلاً لتمثيل الفرق حيث يقابل كل فريق مع باقي الفرق ، ويقوم بالعد أثناء المقابلة . · ومنهم من مثلها بطريقة شبه محسوسة حيث رسم عشرة نقاط ، ثم وصل كل نقطة بباقي النقاط بمنحنى ، ثم قام بعد المنحنيات . · ومنهم من مثلها بجدول . ثانياً : اختلفت إجابات التلاميذ على هذه المشكلة ، حيث استخدم التلاميذ طرقاً واستراتيجيات مختلفة في الحل ، نذكر منها مثلاً : · الحل الأول : باستخدام استراتيجية المحاولة والخطأ المنظمة ، فبعد تمثيل المشكلة بطريقة محسوسة أو شبه محسوسة أو بالجدول ؛ قام بعدّ جميع الاحتمالات الممكنة بطريقة منظمة حتى وصل إلى أن : عدد المباريات = 45 مباراة . · الحل الثاني : باستخدام استراتيجية البحث عن نمط، فبعض التلاميذ بعد تمثيل المشكلة والبدء بعد المباريات ، اكتشف النمط الذي يسير عليه عدد المباريات ، حيث لاحظ أن عدد المباريات هي : 9 ، 8 ، 7 ، .. . فيستنتج أن : عدد المباريات = 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 = 45 مباراة . · الحل الثالث : باستخدام استراتيجية تبسيط المسألة، فمن الطلاب من قام بتبسيط المسألة عن طريق التخفيف من شروط المسألة ، حيث اعتبر أن كل فريق سيلعب مباراتين مع الفريق الآخر ، مما يعني أن كل فريق من الفرق العشرة سيلعب 9 مباريات ، فيكون عدد المباريات = 10 × 9 = 90 مباراة ، ثم عاد إلى شرط المسألة " بحيث يلعب كل فريق مع كل فريق آخر مرة واحدة فقط " ، فحذف نصف عدد المباريات ، فيكون عدد المباريات = 90 ÷ 2 = 45 مباراة . · الحل الرابع : ومنهم من بدأ في الحل عن طريق معالجة حالات خاصة وبسيطة، فبدأ أولاً بفريق ليجد أن عدد المباريات هو صفر، ثم بفريقين ليجد أن عدد المباريات هو مباراة واحدة، ثم بثلاث فرق حيث يجد أن عدد المباريات اللازمة هو 3 مباريات، ثم بأربعة فرق حيث يجد أن عدد المباريات هو 6 مباريات . وقد ينشئ جدولاً كما يلي:
وباستخدام طريقة الفروق يصل إلى استنتاج الحد النوني في هذه المتتابعة ، والذي يعطى بالقانون =
حيث، ق : هي عدد الفرق. فيجد أن عدد المباريات التي يلعبها عشرة فرق = 45 مباراة . · الحل الخامس : باستخدام بناء جملة رياضية ، حيث يرى أن المشكلة تعني باللغة الرياضية : كم زوجاً من الفرق يمكن اختياره من بين عشرة فرق، أي: نريد حساب 10 توافيق 2، والتي تساوي 45 مباراة .
مثال (2) : أوجد مجموع أول مائة عدد فردي موجب . الحل : 1-فهم المشكلة : المعطيات : أول مائة عدد فردي . المطلوب : إيجاد مجموع هذه الأعداد . 2-وضع خطة للحل : الاستراتيجية المناسبة لحل هذه المشكلة هي البحث عن نمط . 3-تنفيذ الخطة : نوجد مجموع أول عددين فردين ، ثم أول ثلاثة أعداد ، ثم أول أربعة أعداد ، ... وهكذا حتى نكتشف النمط ، وذلك بالاستعانة بالجدول التالي ( كاستراتيجية مساعدة ) :
من خلال ما سبق يمكن استنتاج أن : 1 + 3 + 5 + 7 + .......... + ( 2ن -1 ) = ن2 4-التأكد من صحة الحل : من خلال الحدود الأولى يمكن التأكد من صحة الحل .
مثال (3) : يدفع صاحب مصنع 7 ريالات للعامل مكافأة إذا لم يتأخر عن دوامه ، ولكنه يخصم منه 5 ريالات في حالة تأخره . وبعد 24 يوماً لم يستلم العامل شيئاً ، ولم يخصم منه شيئاً . فكم يوماً حضر مبكراً وكم يوماً حضر متأخراً ؟ الحل : الاستراتيجية المناسبة لحل هذا السؤال هي : استراتيجية بناء جملة رياضية . لنفترض أن : عدد الأيام التي حضرها مبكراً = x وعدد الأيام التي حضرها متأخراً = y
وبضرب المعادلة (1) في 5 نجد :
وبجمع المعادلتين نحصل على قيمة x كما يلي :
وبالتعويض في المعادلة (1) نحصل على قيمة y :
إذاً : حضر العامل 10 أيام مبكراً وتأخر 14 يوماً .
طريقة أخرى للحل : يمكن طرح هذا السؤال على المرحلة الابتدائية ، وفي هذه الحالة لا يمكن استخدام استراتيجية بناء جملة رياضية خاصة وأن الحل السابق يستخدم معادلتين في متغيرين من الدرجة الأولى . وفي هذه الحالة نبحث عن استراتيجية مناسبة للمرحلة الابتدائية ، ألا وهي : استراتيجية المحاولة والخطأ المنظمة أو المتقدمة . والتي تفترض تقدير حل ممكن والاستفادة منه في الوصول إلى الحل الصحيح كما يلي :
لنفترض أن العامل حضر 12 يوما مبكراً و 12 يوماً متأخراً ، فيكون لديه في هذه الحالة :
وعليه فإن هذا الجواب غير صحيح ، فنقوم بعملية استبدال عدد من الأيام التي حضرها مبكراً بأيام حضرها متأخراً . ( لاحظ أنَّ : التفكير المنطقي يشير إلى أنَّ عدد أيام الحضور مبكراً أقل من عدد أيام التأخر ، وعليه فإنَّ التفكير المنطقي يجعلنا نفترض أن العامل حضر مبكراً 11 يوماً أو 10 أيام – مثلاً – وهذا قد يقودنا أحياناً إلى اختصار الحل )
فكم يوماً نحتاج في عملية الاستبدال لكي نحصل على الجواب الصحيح ؟ هذا يتطلب استخدام التفكير المنطقي ، كما يلي : إذا استبدلنا يوماً واحداً كم ينقص الرقم ؟ بعد التفكير أو من خلال التجربة نجد أنه ينقص 12 يوماً ( 5+7 ) ، وعليه فنستبدل يومين فقط لأن الجواب السابق = 24 . فيصبح العامل حضر 10 أيام مبكراً و 14 يوماً متأخراً .
مثال4 : إذا قاد أحمد سيارته بسرعة 100 كم/س ؛ فإنه يصل المطار قبل موعد الرحلة بساعة واحدة ، وإذا قاد سيارته بسرعة 80 كم/س يتأخر عن موعد الرحلة بساعة فما المسافة من المنزل إلى المطار ؟ الحل : الاستراتيجية المناسبة لحل هذا السؤال هي : استراتيجية بناء جملة رياضية . لنفرض أن : المسافة = x . إذاً : الزمن اللازم بالنسبة للسرعة الأولى =
وبما أنَّ : الفرق بين الزمنين = 2 . إذاً :
طريقة أخرى للحل : يمكن حل هذه المشكلة بطريقة أخرى باستخدام استراتيجية بناء جملة رياضية . لنفرض أن : المسافة = F . الزمن اللازم بالنسبة للسرعة الأولى = x . الزمن اللازم بالنسبة للسرعة الأولى = x + 2 . بما أن المسافة ثابتة ، أي : F = F 100 x = 80 (x +2) 100 x = 80 x + 160 20 x = 160 x = 8 إذاً : الزمن الذي يلزم لوصول أحمد في سرعته الأولى = 8 ساعات . وعليه فإن : المسافة من المنزل إلى المطار = السرعة × الزمن . = 100 × 8 = 800 كم .
مثال5 : ما عدد الكراسي التي يمكن وضعها على ن طاولة متجاورة موضوعة بالشكل التالي :
الحل : الاستراتيجية المناسبة لحل هذه المشكلة ، استراتيجية البحث عن نمط ، حيث نبحث في بعض الأمثلة الخاصة البسيطة ، مثلاً : س1) ما عدد الكراسي التي يمكن وضعها على الطاولة التي أمامك ؟
لاحظ أن كل طاولة في الطرف يمكن وضع خمس كراسي عليها. إذاً : عدد الكراسي = 2×5 = 10 كراسي .
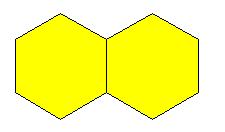
س2) ما عدد الكراسي التي يمكن وضعها على الطاولة التي أمامك ؟
لاحظ أن كل طاولة في الطرف يمكن وضع خمس كراسي عليها وكل طاولة في المنتصف يمكن وضع أربع كراسي :. عدد الكراسي = 2×5 + 4 = 14 كرسي
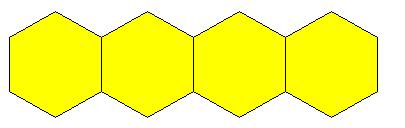
س3) ما عدد الكراسي التي يمكن وضعها في على الطاولة التي أمامك ؟
لاحظ أن كل طاولة في الطرف يمكن وضع خمس كراسي عليها وكل طاولة في المنتصف يمكن وضع أربع كراسي إذاً : عدد الكراسي = 2×5 + 2×4 = 18 كرسي س4)بناءً على ما سبق كم عدد الكراسي التي يمكن وضعها على عشر طاولات بجانب بعضها؟ إذاً : عدد الكراسي = 2×5 + 8×4 = 42 كرسي اكتشاف النمط : من استعراض الأمثلة السابقة نكتشف النمط : حيث نلاحظ أن عدد الكراسي التي يمكن وضعها على ن طاولة متجاورة هو : عدد الكراسي = 2 × 5 + ( ن - 2 ) × 4 =10 + 4ن - 8 = 4 ن + 2
مثال 6 : يحتاج أحمد للذهاب من منزله إلى المدرسة راكباً دراجته إلى 90 دقيقة أقل من مما لو سار على قدميه فإذا استخدم دراجته لمدة 25 دقيقة ثم تعطلت فتركها وواصل سيره على قدميه فوصل إلى المدرسة بعد 110 دقيقة من لحظة تركه للدراجة، كم من الوقت يحتاجه أحمد للذهاب من البيت إلى المدرسة ماشياً؟ الحل : الاستراتيجية المناسبة لحل هذه المشكلة هي بناء معادلة رياضية ، فنفرض أن : أحمد يحتاج لزمن قدره x للوصول للمدرسة من البيت بالدراجة . أحمد يحتاج لزمن قدره x +90 للوصول للمدرسة من البيت ماشياً .
إذاً :
المسافة التي قطعها بالدراجة + المسافة التي قطعها على الأقدام = المسافة بين البيت والمدرسة
وبالقسمة على
وهذا الحل مرفوض لأن الزمن لا يكون بالسالب .
إذاً يحتاج أحمد إلى : = 75 + 90 165 دقيقة .
مثال 7 : في محل الفاكهة سعر حبة الموز ريال واحد وكل 3 تفاحات بـ 5 ريالات وكل 4 برتقالات بـ 5 ريال اشترى خالد 20 حبه من كل أنواع الفاكهة بـ 25 ريال فكم حبه من كل نوع اشترى خالد ؟ الحل : يمكن حل هذه المشكلة عن طريق عمل جدول يمثل جميع الاحتمالات الممكنة لعدد الموز والتفاحات والبرتقالات مع إيجاد مبلغ الشراء، فنستخدم طريقة المحاولة والخطأ المنظمة حتى نصل للحل الذي يحقق الشرط الوارد في المشكلة. فنبدأ أولاً باختيار عدد البرتقالات من مضاعفات العدد 4 وعدد التفاحات من مضاعفات العدد 3 وما يتبقى من العدد 20 هو عدد الموز كما يلي:
إذاً اشترى خالد 10 موزات و6 تفاحات و4 برتقالات .
مثال 8 : في الشكل متوازي أضلاع مساحته =120 م2 فيه: هـ تقع في منتصف [ أ د] أحسب : 1) مساحة الشكل أ ب م هـ 2) مساحة الشكل هـ م د 3) مساحة الشكل ب م جـ 4) مساحة الشكل د م جـ
الحل : الاستراتيجية المناسبة لحل هذه المشكلة هي بناء جملة رياضية . من الواضح أنَّ : · مساحة المثلث أ ب د = نصف مساحة الشكل كاملاً . إذاً : مساحته = 60 م2 ( لأن مساحة الشكل كاملاً = 120 م2 ) إذاً : المثلث الأخضر + المثلث الأزرق = 60 · وبالمثل مساحة المثلث د ب ج = نصف الشكل . إذاً : مساحته = 60 م2 إذاً : المثلث الأحمر + المثلث الأصفر =60
ومن الواضح أيضاً أن : المثلثان هـ م د ، م ب جـ متشابهان لأن : · الزاوية م 1 = الزاوية م 3 ( متقابلتان بالرأس ) . · الزاوية هـ 2 تساوي الزاوية جـ2 ( بالتبادل ) · وكذلك بالمثل د1 و ب2 . ونسبة التشابه بين المثلثين هي 2: 1 . إذاً : مساحة الشكل ب م جـ = 4 × مساحة الشكل هـ م د . الآن نكون المعادلات التالية : الأخضر + الأزرق = الأحمر + الأصفر =60 (1) الأصفر = 4 × الأخضر (2) الأخضر + الأحمر = 30 = نصف الشكل هـ ك جـ د (3)
بالتعويض من 2 في 1 نجد : الأخضر + الأزرق = الأحمر + 4 × الأخضر الأزرق = الأحمر + 3 × الأخضر
ومن المعادلة رقم (3) : الأحمر = 30 – الأخضر إذاً : الأزرق = ( 30 – الأخضر ) + 3 × الأخضر الأزرق = 30 + 2 × الأخضر
ومن المعادلة رقم (1) : الأخضر + الأزرق = 60 إذاً : الأزرق = 30 + 2 × ( 60 – الأزرق ) 3×الأزرق=150 الأزرق = 50 م2 الأخضر = 10 م2 الأصفر = 4 × الأخضر =40 م2 الأحمر = 30 – الأخضر = 30 – 10 =20 م2
التأكد من الحل : الأخضر + الأزرق + الأحمر + الأصفر = 40 + 20 + 10 + 50 =120 م2 = مساحة متوازي الأضلاع
مثال 9 : إذا كانت أ1 هي مساحة مثلث متطابق الأضلاع ، أ2 هي مساحة المثلث الذي ينتج من توصيل منتصفات أضلاع هذا المثلث ، أ3 هي مساحة المثلث الذي ينتج من توصيل منتصفات أضلاع المثلث الثاني وهكذا . أوجد مجموع المتسلسلة : أ1 + أ2 + أ3 + ……. ؟ الحل: - المعطيات: أ1 : مساحة مثلث متطابق الأضلاع ، أ2 : مساحة المثلث الذي ينتج من توصيل منتصفات أضلاع هذا المثلث ، أ3 : مساحة المثلث الذي ينتج من توصيل منتصفات أضلاع المثلث الثاني وهكذا - المطلوب: إيجاد مجموع أ1 + أ2 + أ3 + ………
الاستراتيجية المناسبة لحل هذه المشكلة هي استراتيجية بناء معادلة رياضية . وذلك من خلال توجيه الأسئلة التالية : إذا فرضنا طول ضلع المثلث الكبير ل فأجب عما يلي : س / ما طول ضلع المثلث الثاني؟ س / ما طول ضلع المثلث الثالث؟ س / أذكر نسبة التشابه بين كل مثلث والمثلث السابق له مباشرة؟ س / أذكر العلاقة بين مساحة كل مثلث ومساحة المثلث السابق له مباشرة؟
إذا فرضنا أن طول ضلع المثلث الأول ل فإنه من خلال المناقشة مع الطلاب يتم التوصل إلى ما يلي:
طول ضلع المثلث الثاني = ل
طول ضلع المثلث الثالث = ل
نسبة التشابه بين كل مثلث والمثلث السابق له =
مساحة أي مثلث = مساحة المثلث السابق له مباشرة.
وبذلك استطعنا أن نوجد علاقة بين مساحة أي مثلث والمثلث السابق له مباشرة ، ومنه نستطيع أن نكتب : أ1 + أ2 + أ3 + ……… = ل + ل + ( ل ) + ……… - هل اكتشفت نوع المتسلسلة السابقة ؟ - ما القانون الخاص بمجموع هذه المتسلسلة ؟ ( يترك إكمال حل المشكلة للقارئ )
مثال 10 : إذا أردنا طلاء هذا الشكل بطلاء خارجي :
فأجب عما يأتي : 1. كم عدد المكعبات التي تصبغ من 3 جهات ؟ 2. كم عدد المكعبات التي تصبغ من جهتين ؟ 3. كم عدد المكعبات التي تصبغ من جهة واحدة ؟ 4. كم عدد المكعبات التي لا تصبغ ؟ الحل : وللإجابة على هذا السؤال نستخدم استراتيجية البحث عن نمط : · كم عدد المكعبات التي تصبغ من 3 جهات؟
عدد المكعبات التي تصبغ من ثلاث أوجه = 8 مكعبات لاحظ أنه بعدد رؤوس المكعب وهي ثابتة لأي مكعب طول حرفه ن مكعب . · كم عدد المكعبات التي تصبغ من جهتين؟
عدد المكعبات التي تصبغ من جهتين لمكعب طول حرفه أربع وحدات = 12 × 2 = 24 مكعب . عدد المكعبات التي تصبغ من جهتين لمكعب طول حرفه ن وحده = 12 × ( ن – 2 ) = 12ن – 24 . · كم عدد المكعبات التي تصبغ من جهة واحدة؟
عدد المكعبات التي تصبغ من جهة واحدة لمكعب طول حرفه أربع وحدات = 6 × ( 2× 2) = 24 مكعب . عدد المكعبات التي تصبغ من جهة واحدة لمكعب طول حرفه ن وحده = 6×( ن-2)×(ن-2) = 6 ( ن2 -4ن + 4 ) = 6ن2 -24ن +24 .
· كم عدد المكعبات التي لن تصبغ ؟ المكعبات التي لن تصبغ = ( ن – 2 )3 مكعب .
مثال 11 : بائع تفاح متجول يجوب القرى لبيع حمولته . وفي يوم ما صادف أن مرت مبيعاته بنمط رياضي عجيب. ففي كل قرية دخلها، يبيع نصف ما معه من صناديق التفاح. وعندما وصل إلى القرية الخامسة ، لم يكن معه سوى صندوق واحد من صناديق التفاح، فباعه وعاد بيته . فكم صندوقاً من التفاح كان معه في بداية الرحلة ؟ الحل : 1- فهم المسألة : المعطيات : نمط البيع كان يتمثل في أن التاجر كان يبيع نصف ما معه في كل قرية. عندما دخل التاجر إلى القرية الخامسة كان معه صندوق واحد من التفاح المطلوب : عدد صناديق التفاح في بداية الرحلة . 2- وضع خطة الحل : نبدأ من القرية الخامسة حيث دخلها التاجر بصندوق واحد من التفاح وهذا العدد يمثل نصف ما كان معه عندما دخل القرية الرابعة . وما كان معه عندما دخل القرية الرابعة يمثل نصف ما كان معه عندما دخل القرية الثالثة ، وهكذا . 3-تنفيذ الخطة : ما كان لديه عندما دخل القرية الخامسة = 1 صندوق ما كان لديه عندما دخل القرية الرابعة = 1×2 = 2 صندوق ما كان لديه عندما دخل القرية الثالثة = 2×2 = 4 صناديق ما كان لديه عندما دخل القرية الثانية = 2×4 = 8 صناديق ما كان لديه عندما دخل القرية الأولى = 2×8 = 16 صناديق إذاً : كان معه 16 صندوق من التفاح في بداية الرحلة .
4- مراجعة الحل : أفضل طريقة لمراجعة الحل هي العمل للأمام . إذا كان معه 16 صندوق عندما دخل القرية الأولى ، فسيبقى معه 8 صناديق للقرية الثانية و 4 صناديق للقرية الثالثة و صندوقان للقرية الثانية وصندوق واحد للقرية الخامسة .
مثال 11 : س /ما هي العلاقة بين الزاويتين x و أ في الشكل التالي ؟
الحل : الزاوية 3 و 4 خارجية بالنسبة للمثلث أ ب ج .
2
بالنسبة للمثلث ب ج هـ فإن
بالتعويض في المساواة ( 2 ) نجد أن :
2 (
2
|