استراتيجيات حل المشكلات

مقدمة  :

الاستراتيجيات هي العمليات أو الخطوات التي يجريها الفرد للوصول إلى حل للمشكلة مستخدماً في ذلك المعلومات والمعارف التي تعلمها سابقاً  .

ويمكن للتلميذ استخدام العديد من الاستراتيجيات للوصول إلى حل المشكلة ، والبحث في استراتيجيات حل المشكلات يعتبر من أكثر جوانب مجال حل المشكلات ثراءً وأهمية ، حتى أن شونفيلد Schoenfield ( 1979م ) يقول : " إذا تمكنا أن نحدد بنجاح استراتيجيات جيدة ومفيدة لحل المشكلات ، فإن العائد بالتأكيد سيكون عظيماً " .

ويمكن تقسيم هذه الاستراتيجيات إلى قسمين :

(1) استراتيجيات عامة : وتشمل :

1-استراتيجية بناء جملة رياضية .

2-استراتيجية المحاولة والخطأ .

3-استراتيجية البحث عن نمط .

4-استراتيجية تبسيط المشكلة .

5-استراتيجية العمل للخلف ( البدء من النهاية ) .

6-استراتيجية التفكير الإبداعي .

(2) استراتيجيات مساعدة : وتشمل :

1-      استراتيجية عمل جدول .

2-      استراتيجية عمل قوائم منظمة .

3-      استراتيجية التمثيل .

4-      استراتيجية عمل نموذج .

وسوف نتناول هذه الاستراتيجيات بشيء من التفصيل مع ضرب أمثلة كافية على هذه الاستراتيجيات .

أولاً : الاستراتيجيات المساعدة :

وهي الاستراتيجيات التي تساعد في فهم المشكلة واستيعابها ، كما تفيد أيضاً في تنظيم المعلومات الواردة فيها وإدراك العلاقات بين هذه المعلومات . فالاستراتيجيات المساعدة تستخدم في الخطوة الأولى من خطوات بوليا لحل المشكلة، وهي خطوة : فهم المشكلة .

(1) استراتيجية عمل جدولMaking a table  :

في حل بعض المشكلات قد يكون إنشاء جدول عاملاً مساعداً في فهم المشكلة ومن ثم اكتشاف طريقة الحل، أو قد يساعد على رؤية نمط معين يلمح إلى الحل . أو على الأقل قد يوحي باستعمال استراتيجية ما .

وفي هذه الاستراتيجية يتم عمل جدول يضم البيانات المعطاة في المشكلة بترتيب معين ، هذا الترتيب يساعدنا في اكتشاف البيانات المفقودة ويوضح ما بينها من علاقات ، مما يقودنا إلى سهولة إدراك العلاقة بين المعطيات والمطلوب وصولاً إلى الحل .

(2)استراتيجية عمل قوائم منظمة Making an organized list:

ويتم فيها تنظيم تفكيرنا حول المشكلة بوضع البيانات المعطاة بطريقة منظمة على شكل قائمة ، وهذا مما يسمح لنا بمراجعة ماذا عملنا ؟ ، وما هي الخطوة المهمة التي نحتاج لعملها لإكمال حل المشكلة . 

(3) استراتيجية التمثيل Act out :

وتأتي فائدة هذه الاستراتيجية من خلال الفرصة التي تتهيأ للتلميذ لرؤية المتغيرات في المشكلة وكذلك العلاقات بين هذه المتغيرات . وهي أنواع فقد يكون :

أ- التمثيل بالمحاكاة :

ويتم بها تمثيل الموقف أو المشكلة في الواقع العملي وتطبيقها على الحياة الواقعية مما يساعد في فهم المشكلة وتسهيل اكتشاف الحل .

هذا يسمح لك بالتّحرّك حول الأشياء، كما يساعد في تذكّر المشكلة وطريقة حلها لكي تكون قادراً على استخدامه ثانية لحلّ المشاكل المتشابهة الأخرى.

مثال: بكم طريقة يمكن ترتيب أربع كتب في رف فارغ بشرط أن يكون كتابان بجانب بعضها دائماً؟

الحل :

يمكن تمثيل هذه الكتب بطريقة حقيقية أمام الطلاب بلصق كتابين دائماً ، ومن ثم حساب عدد حالات الترتيب

 سنجد أن عدد حالات الترتيب = 6 حالات .

ب- التمثيل باستخدام المجسمات أو النماذج المحسوسة

 Act out by Using objects Or A concrete model  :

ويتم بها تمثيل موقف المشكلة عن طريق نموذج مادي محسوس .

هذا التمثيل يتيح لنا تحريك الأجسام بسهولة مما قد يكون له أثر كبير في اكتشاف الحل أو تذكر المشكلة المشابهة لهذه المشكلة.

ج- التمثيل بالرسم Act out by drawing :

ويتم بها التعبير عن الموقف وما يتضمنه من معطيات وشروط وعلاقات برسم شكل تخطيطي أو بياني أو صورة توضيحية مما يساعد في فهم واستيعاب المشكلة .

وفي الحقيقة ما هي إلا تحويل للمشكلة من المستوى المجرد إلى مستوى شبه المحسوس، وفي هذا المستوى الأخير قد تكون المعلومات والعلاقات بين هذه المعلومات بارزة أكثر مما قد يوحي للتلميذ بأشياء تفيده في إنشاء خطة الحل .

هذه الاستراتيجية مفيدة خصوصاً في المشكلات التي تتضمن خرائط ، أو رسومات هندسية .

مثال :

ينظر رجل إلى مئذنة بزاوية ارتفاع =60^ه ، أحسب ارتفاع المئذنة عن سطح الأرض علما بأن طول الرجل 1.7 م ، ويقف على بعد 20 م من قاعدة المئذنة ؟

الحل :

يمكن رسم شكل هندسي يساعد في فهم هذه المشكلة وحلها حيث تظهر في هذا الشكل المعلومات والعلاقات بين هذه المعلومات بشكل بارزة مما قد يوحي للتلميذ بأشياء تفيده في إنشاء خطة الحل .

والشكل التالي يوضح ذلك :

ثم يسهل على التلميذ معرفة العلاقة بين معطيات المسألة واستخدام النسب المثلثية لإيجاد ارتفاع المئذنة .

( سوف يستخدم التلميذ النسبة : ظا هـ  = المقابل ÷ المجاور ) .

 (4) استراتيجية عمل نموذجMaking model  :

ويتم بها دراسة حالات خاصة من المشكلة المراد حلها ، ثم حل المسألة عن طريق تعميم نتائج الحالات الخاصة . 

 ثانياً : الاستراتيجيات العامة :

الاستراتيجية : هي خطة عامة محددة المعالم للوصول إلى حل المشكلة ، وهذه الاستراتيجيات تستخدم في الوصول إلى حل المشكلة . فالاستراتيجيات العامة تستخدم في الخطوة الثانية من خطوات بوليا لحل المشكلة ، وهي خطوة : إنشاء خطة لحل المشكلة.

 (1) استراتيجية بناء جملة رياضية

  Building Mathematical Sentence :

وهي من أقوى الاستراتيجيات ، حتى أن كثيراً من المشكلات يمكن حلها عن طريق هذه الاستراتيجية ، وكثر استعمالها مما جعلها أول استراتيجية تتبادر إلى الذهن عندما نريد حل مشكلة ما . ورغم قوة هذه الاستراتيجية وشيوعها إلا أن هناك ملاحظتان يجب التنبيه عليهما :

1.  أنها تتطلب في كثير من الأحيان رياضيات عالية لاستخدامها .

2.  ولهذا يصعب استخدامها في رياضيات المرحلة الابتدائية .

خطواتها: يقوم التلميذ بـ :

1)  ترجمة المشكلة اللفظية إلى جملة رياضية.

2)  حل الجملة الرياضية لإيجاد قيمة أو قيم المجهول والذي يمثل حل المشكلة.

متى تستخدم هذه الاستراتيجية : تكون هذه الاستراتيجية مفيدة : إذا استطعنا أن نجد علاقة تربط بين متغيرات المشكلة ، وكانت الجملة الرياضية المكونة تناسب مستوى التلميذ.

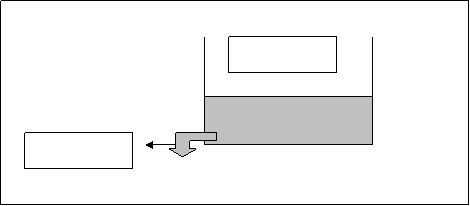
مثال 1 :

ينصب الماء في خزان بمعدل 50 لتراً قي الساعة ، ويتسرب منه بمعدل 15 لتراً في الساعة . فما الزيادة في حجم الماء قي الخزان بعد مضي 3 ساعات ؟

الحل :

1- فهم المسألة :

المعطيات : معدل الصب = 50 لتراً قي الساعة .

   معدل التسرب = 15 لتراً قي الساعة . الزمن 3 ساعات .

المطلوب : مقدار الزيادة في حجم الماء بعد 3 ساعات .

2- وضع خطة للحل :

يمكن رسم نموذج للمسألة كالتالي :

وباستخدام استراتيجية بناء معادلة رياضية ، نستطيع كتابة المعادلة التالية :

معدل زيادة حجم الماء = معدل الصب – معدل التسرب

       مقدار الزيادة = معدل زيادة حجم الماء × الزمن

3- تنفيذ الخطة :

       معدل زيادة حجم الماء = 50 – 15 = 35 لتراً في الساعة

       مقدار الزيادة = 35 × 3 = 105 لتراً .

4- مراجعة الحل :

       هل كان هذا هو المطلوب ؟ نعم

       هل يبدو الجواب معقولاً ؟ نعم

       هل يمكن التأكد من الجواب بدقة ؟ نعم

       مقدار الصب في 3 ساعات = 50 × 3 = 150 لتراً

       مقدار التسرب في 3 ساعات = 15 × 3 = 45 لتراً

مقدار الزيادة=مقدار الصب – مقدار التسرب =150- 45 =105لتراً .

مثال 2 :

إذا كان شراء مسطرتين و 4 أقلام يكلف أكثر من شراء قلمين و 4 مساطر بريالين . فما الفرق بين سعر القلم وسعر المسطرة ؟

الحل :

وباستخدام استراتيجية بناء معادلة رياضية ، نضع : مسطرة = م  ،  قلم = ق

فتتكون لدينا المعادلة التالية :

2 م + 4 ق = 4 م + 2ق + 2

2 ق = 2 م + 2

ق = م + 1

ق – م = 1

الفرق بين سعر القلم وسعر المسطرة هو ريال واحد .

(2) استراتيجية المحاولة والخطأ Trial and error  :

" وتتمثل ببساطة في تطبيق العمليات الممكنة على المعلومات المعطاة ضمن المشكلة، ويلجأ إليها بعض التلاميذ ذوي الخبرة القليلة في حل المشكلات " .

خطواتها: يقوم التلميذ بـ :

3)  تخمين جميع الاحتمالات الممكنة لحل المشكلة.

4) ثم فحص واختبار مدى صلاحية هذه الاحتمالات لحل هذه المشكلة، وذلك بتجريب كل احتمال على حدة إلى أن يتم اختيار الاحتمال المحقق منها.

متى تستخدم هذه الاستراتيجية : تكون هذه الاستراتيجية مفيدة :

1)    عندما تتطلب المشكلة اختيار حل وحيد من مجموعة كثيرة من الحلول الممكنة.

2)    عندما تحوي المشكلة أعداداً كثيرة أو بيانات كثيرة.

ويمكن تقسيمها إلى أقسام :

أ‌-     المحاولة والخطأ العشوائية trial and error : حيث لا يكون هناك نظام معين يسير عليه التلميذ في اختياره للاحتمالات الممكنة . ولاشك أن هذه الاستراتيجية غير عملية إذا كان اختيار الحلول ليس له نظام معين ، أو غير مبنيٍّ على أساس منطقي مما قد يؤدي إلى صعوبة وصول التلميذ إلى الحل الصحيح ، بل قد يختبر حلاً واحداً أكثر من مرة وهو لا يشعر ، خاصة إذا كانت الحلول الممكنة للمشكلة كثيرة جداً ، وهذا ما جعل البعض يشكك في اعتبارها ضمن استراتيجيات حل المشكلات .

ب‌-   المحاولة والخطأ المنظمة Systematic trial and error : وذلك بأن يتم تنظيم المحاولات التي نختبر صلاحيتها لحل المشكلة . ونستفيد من هذا التنظيم أمرين هما:

·      أننا نضمن عدم إغفال أي احتمال بلا اختبار .

·      كما نضمن أيضاً عدم تكرار اختبار احتمال ما أكثر من مرة .

إلا أنها تكون غير عملية وتتطلب وقتاً طويلاً إذا كانت الاحتمالات الممكنة لحل هذه المشكلة كثيرة . وهنا يجب الانتباه إلى أنه من غير العملي أن تكون كافة المحاولات عشوائية وغير مرتبطة ببعضها ، لأن ذلك يقود إلى إطالة الزمن اللازم للحل . والصحيح أن تبنى كل محاولة على ما سبقها من المحاولات من أجل الاقتراب من الحل الصحيح . وهنا يأتي دور المعلم في الاستفادة من هذه الطريقة الشائعة حيث يبدأ منها ، ثم يطورها إلى طرق منظمة وأكثر فعالية ، كما في :

ت‌-   المحاولة والخطأ المتقدمة Advanced trial and error : وذلك بمحاولة تقليل عدد الاحتمالات الممكنة وتضييق نطاق البحث إلى أقصى حد ممكن عن طريق الاستفادة من المنطق الرياضي . ويتضمن ذلك اعتبار كافة احتمالات الحل ثم حذف الاحتمالات غير المنطقية مما يؤدي إلى تقليل عدد الاحتمالات التي نحتاج لاختبارها . وهذا يتطلب من التلميذ أن يقوم بتحليل المشكلة ، ومن ثم الاستفادة من معلومات ذات صلة بموضوع المشكلة في استبعاد بعض الاحتمالات ، وقد يستفيد أحياناً من نتائج بعض المحاولات التي قام بها لحل هذه المشكلة .

وتسمي بعض المراجع هذه الاستراتيجية بأسماء أخرى مثل : المحاولة والخطأ الاستدلالية Inferential trial and error ، أو المحاولة والخطأ المنطقية ، أو اعتبار كافة الإمكانيات ثم الحذف .

ث‌-   التخمين الذكي والتأكد Intelligence guessing and testing : وذلك بأن يكون لدى التلميذ حدس قوي أو ملكة جيدة في توقع الحل مباشرة فيقوم باختباره ، وهذا في الحقيقة يعتمد على مراحل عقلية متقدمة تنم عن قوة في التفكير . وتسميها بعض المراجع :

التقدير التقريبي والفحص Estimation and check : فنقوم بتقدير لحل المشكلة دون إجراء للعمليات الحسابية بالأسلوب الخوارزمي المعتاد ، أو تحديد المدى الذي يقع فيه الناتج ، وهذا الناتج التقريبي يتم اختبار صحته في ضوء علاقته بالناتج المضبوط .

مثال 1 : عدد أكبر من 60 وأقل من 90 يقبل القسمة على 3 بدون باق . الفرق بين الرقمين المكونين لرمزه هو 2 . ما ذلك العدد ؟

الحل :

الاستراتيجية المناسبة لحل هذه المشكلة ، هي استراتيجية المحاولة والخطأ ، ولكن :

·  عند استخدامنا لاستراتيجية المحاولة والخطأ العشوائية ، قد يتطلب ذلك منا 29 محاولة كحدٍ أقصى حتى نصل إلى الحل الصحيح .

·  وعندما نستخدم استراتيجية المحاولة والخطأ المنظمة ؛ فسنكتب جميع الأعداد المحصورة بين العددين 60 و 90 ، وهي :

61 , 62 , 63 , 64 , 65 , 66 , 67 , 68 , 69 , 70 , 71 , 72 , 73 , 74 , 75 , 76 , 77 , 78 , 79 , 80 , 81 , 82 , 83 , 84 , 85 , 86 , 87 , 88 , 89 .

وسنقوم باختبار هذه الأعداد بطريقة منظمة حتى نصل إلى العدد الذي يحقق الشرطين : " يقبل القسمة على 3 بدون باق ، والفرق بين الرقمين المكونين لرمزه هو 2 " . وسيتطلب ذلك منا 15 محاولة حتى نصل إلى الحل الصحيح .

·  أما عندما نستخدم استراتيجية المحاولة والخطأ المتقدمة وذلك من خلال الاستفادة من فكرة اعتبار كافة الإمكانيات ثم حذف الاحتمالات غير المنطقية ( وهي الأعداد التي لا تقبل القسمة على 3 أو التي لا يكون الفرق بين الرقمين المكونين لها مساوياً لاثنين ) فسنقوم بما يلي :

- نعمل قائمة بكافة رموز الأعداد الأكبر من 60 والأصغر من 90 :

61 , 62 , 63 , 64 , 65 , 66 , 67 , 68 , 69 , 70 , 71 , 72 , 73 , 74 , 75 , 76 , 77 , 78 , 79 , 80 , 81 , 82 , 83 , 84 , 85 , 86 , 87 , 88 , 89 .

- ثم نحذف تلك الأعداد التي لا يكون الفرق بين الرقمين المكونين لرمزيها مساويا لاثنين . فيتبقى لدينا الأعداد :

64 , 68 , 75 , 79 ، 86 .

- ثم نحذف أي عدد لا يقبل القسمة على 3 فيتبقى : 75 فقط . إذن الإجابة هي 75 .

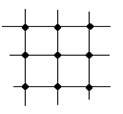
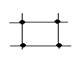
مثال 2 :

رتب الأعداد من 1-9 في المثلث التالي بحيث يكون مجموع الأعداد في كل ضلع يساوي 17.

الحل :

الاستراتيجية المناسبة لحل هذه المشكلة ، هي استراتيجية المحاولة والخطأ ، ولكن :

·  قد نبدأ في حل هذه المشكلة بتجريب مجموعة من الحلول الممكنة عشوائياً ، وهذه تسمى استراتيجية المحاولة والخطأ العشوائية .

·  وقد نقوم بتنظيم هذه المحاولات ، فنقوم مثلاً بتثبيت ثلاثة أرقام في الأركان ثم تجريب الأرقام الباقية بانتظام ، وهذه تسمى المحاولة والخطأ المنظمة . إلا أنه باستخدام هذه الاستراتيجية قد لا نصل إلى الحل الصحيح إلا بعد 181440 محاولة . مما يعني ضعف هذه الاستراتيجية في حل هذه المشكلة لأنها تتطلب وقتاً وجهداً كبيرين .  

·  وقد نستفيد من التفكير المنطقي في المعلومات المعطاة في المشكلة في تقليل عدد المحاولات وتضييق نطاق البحث ، فنقول مثلاً :

o    مجموع الأعداد من 1-9 = 45 .

o    بينما مجموع الأعداد على الأضلاع الثلاثة = 3 × 17 = 51 .

o    الفرق بين المجموعين هو 6 .

o    يأتي هذا الفرق من خلال تكرار الأرقام الموجودة في الأركان عند إجراء عملية الجمع .

o    إذاً الأرقام التي في الأركان يجب أن يكون مجموعها = 6 .

o    هذه الأرقام هي : 1 ، 2 ، 3 .

وهكذا يكون التلميذ قد اختصر المحاولات الممكنة من 181440 إلى 360 محاولة ، فإذا استفاد من التفكير المنطقي مرة أخرى فقد يختصر عدد المحاولات الممكنة إلى أقل من ذلك بكثير ، فيقول مثلاً :

o    يجب توزيع الأرقام الكبيرة أولاً ( 9 ، 8 ، 7 ) على الأضلاع الثلاثة .

o  نضع العدد 9 في أحد الضلعين اللذين يشترك فيهما العدد 1 ، وذلك لإعادة موازنة مجموع الأرقام على الأضلاع الثلاثة .

o  نوزع باقي الأرقام ( 6 ، 5 ، 4 ) على باقي الأضلاع لكي يكون المجموع 17 في كل ضلع. وبهذا يكون التلميذ قد اختصر المحاولات الممكنة من 360 محاولة إلى ثلاث محاولات فقط .

أخيراً : إن هذا النوع من الاستراتيجيات أسلوب قوي جداً وفعّال في سرعة الوصول إلى الحل في بعض المشكلات إلا أنه يتطلب مهارة وملكة خاصة لكي نجري التحليل المطلوب ونستفيد من التفكير المنطقي ، ومن ثم نختصر عدد الاحتمالات إلى أقصى حد ممكن .

  مثال 3 :

  مستطيل مساحته تساوي محيطه ( عددياً ) وبعداه مختلفان وطول كلاً منهما عبارة عن عدد صحيح . أوجد بعديه ؟ ( علماً بأن طول المستطيل أقل من 10سم ) .

 الحل :

 يمكن حل هذه المشكلة عن طريق عمل جدول يمثل جميع الاحتمالات الممكنة لطول وعرض المستطيل مع إيجاد المساحة والمحيط لهذه الاحتمالات ، فنستخدم طريقة المحاولة والخطأ المنظمة حتى نصل للحل الذي يحقق الشرط الوارد في المشكلة كما يلي :

 يتضح من السطر الأخير في الجدول أنه إذا كان طول المستطيل = 6 سم ،  وعرضه = 3 سم ؛ فإن مساحته = 18 سم² ، و محيطه = 18 سم  وهي تعتبر حلاً لهذه المشكلة  .

 مثال 4 :

 كيف يمكن أن تزرع 10 شتلات في 5 خطوط مستقيمة بحيث يضم كل خط 4 شتلات ؟

 الحل :

      المحاولة الأولى : 

فشلت المحاولة !

      هل اشترطت المسألة أن تكون الخطوط متوازية ؟

      الجواب : لا

المحاولة الثانية :

فشلت المحاولة !

المحاولة الثالثة :

محاولة ناجحة !                 

أعد حل المسألة بحيث تكون المعطيات :

 12 شتلة في 6 صفوف بأربع شتلات لكل منها .

19 شتلة في 9 صفوف بخمس شتلات لكل منها .

مثال 3  :

ثمن الكره الصغيرة 3 ريالات وثمن الكره الكبيرة 5 ريالات . اشترى بدر 10 كرات بمبلغ 36 ريال . فكم كره صغيرة وكم كره كبيره اشترى بدر ؟  

الحل :

1-فهم المسألة :

المعطيات : ثمن الكره الصغيرة = 3 ريال

           ثمن الكره الكبيرة = 5 ريال

المطلوب : كم كره صغيرة وكم كره كبيره اشترى بدر

2-وضع خطة الحل :

إستراتيجية المحاولة والخطأ . نفترض عددا من الكرات الصغيرة وعددا من الكرات الكبيرة بحيث يكون المجموع 10 كرات . نحيب ثمن الكرات الصغيرة وثمن الكرات الكبيرة ثم نجمع . اذا كان الناتج 36 ريال ، فالحل صحيح ، واذا كان الناتج اقل من 36 ريال . نزيد عدد الكرات الكبيرة . اما اذا كان الناتج اكبر من 36 ريال ، نقلل عدد الكرات الكبيرة .

3-تنفيذ الخطة :

المحاولة الأولى :

   افترض أن عدد الكرات الصغيرة = 5 كرات

   افترض أن عدد الكرات الكبيرة = 5 كرات

السعر = 5×3 + 5×5 = 40 ريال

زاد المبلغ عن 36 ريال . إذن لابد من إنقاص عدد الكرات الكبيرة .

المحاولة الثانية :

   افترض أن عدد الكرات الصغيرة = 6 كرات

   افترض أن عدد الكرات الكبيرة = 4 كرات

السعر = 6×3 + 4×5 = 38 ريال

زاد المبلغ عن 36 ريال . إذن لابد من إنقاص عدد الكرات الكبيرة .

المحاولة الثالثة :

   افترض أن عدد الكرات الصغيرة = 7 كرات

   افترض أن عدد الكرات الكبيرة = 3 كرات

السعر = 7×3 + 3×5 = 36 ريال

إذن الإجابة هي 7كرات صغيرة و3 كرات كبيرة .

4-مراجعة الحل :

       هل تمت الإجابة على السؤال ؟ نعم

       تأكد أن عدد الكرات هو 10 .

       عدد الكرات = 7+3= 10 كرات .

       تأكد أن السعر الكلي = 36 ريال .

       السعر الكلي = 7×3 + 3×5 = 36 ريال

مثال 4  :

ثمن الكره الصغيرة 3 ريالات وثمن الكره الكبيرة 5 ريالات . اشتر بدر 10 كرات بمبلغ 36 ريال . فكم كره صغيرة وكم كره كبيره اشترى بدر ؟  

الحل :

1-فهم المسألة :

   المعطيات : ثمن الكره الصغيرة = 3 ريال

               ثمن الكره الكبيرة = 5 ريال

   المطلوب : كم كره صغيرة وكم كره كبيره اشترى بدر

2-وضع خطة الحل :

إستراتيجية المحاولة والخطأ . نفترض عددا من الكرات الصغيرة وعددا من الكرات الكبيرة بحيث يكون المجموع 10 كرات . نحيب ثمن الكرات الصغيرة وثمن الكرات الكبيرة ثم نجمع . اذا كان الناتج 36 ريال ، فالحل صحيح ، واذا كان الناتج اقل من 36 ريال . نزيد عدد الكرات الكبيرة . اما اذا كان الناتج اكبر من 36 ريال ، نقلل عدد الكرات الكبيرة .

3-تنفيذ الخطة :

المحاولة الأولى :

   افترض أن عدد الكرات الصغيرة = 5 كرات

   افترض أن عدد الكرات الكبيرة = 5 كرات

السعر = 5×3 + 5×5 = 40 ريال

زاد المبلغ عن 36 ريال . إذن لابد من إنقاص عدد الكرات الكبيرة .

المحاولة الثانية :

   افترض أن عدد الكرات الصغيرة = 6 كرات

   افترض أن عدد الكرات الكبيرة = 4 كرات

السعر = 6×3 + 4×5 = 38 ريال

زاد المبلغ عن 36 ريال . إذن لابد من إنقاص عدد الكرات الكبيرة .

المحاولة الثالثة :

   افترض أن عدد الكرات الصغيرة = 7 كرات

   افترض أن عدد الكرات الكبيرة = 3 كرات

السعر = 7×3 + 3×5 = 36 ريال

إذن الإجابة هي 7كرات صغيرة و3 كرات كبيرة .

4-مراجعة الحل :

       هل تمت الإجابة على السؤال ؟ نعم

       تأكد أن عدد الكرات هو 10 .

       عدد الكرات = 7+3= 10 كرات .

       تأكد أن السعر الكلي = 36 ريال .

       السعر الكلي = 7×3 + 3×5 = 36 ريال

(3) استراتيجية البحث عن نمطLook for a pattern  :

وتتمثل هذه الاستراتيجية بفحص حالات خاصة مختارة من المشكلة ، ثم البحث بدقة عن النمط الذي تسير عليه هذه الحالات الخاصة ، ومن ثم تعميم ذلك على المشكلة المطلوبة . وهذه الأنماط قد توجد في الأعداد أو الأشكال أو السلوك ، وكثيراً ما يحتاج التلميذ إلى الاستعانة بعمل جدول أو قائمة (كاستراتيجية مساعدة) في الكشف عن هذا النمط .

خطواتها : يقوم التلميذ بـ :

1)  فحص حالات خاصة مختارة للمشكلة .

2)  اكتشاف النمط الذي تسير عليه هذه الحالات الخاصة .

3)  ومن ثم تعميم نتائج هذه الحالات الخاصة على المشكلة الأصلية .

متى تستخدم : هذه الاستراتيجية مفيدة :

عندما يكون المطلوب هو حل عام للمشكلة ( قانون عام ) ، وبدراسة حالات خاصة منها يمكن أن تكون مفتاحاً لاكتشاف الحل ( النمط ) ، وهي أفضل أنواع الاستراتيجيات في مسائل المتتابعات والمتسلسلات.

مثال 1 :

ما مجموع قياسات الزوايا الداخلية لمضلع عدد أضلاعه 20 ؟

الحل :

1-فهم المسألة :

   المعطيات : عدد أضلاع المضلع = 20 ضلع .

   المطلوب : ما مجموع قياسات زواياه الداخلية .

2-وضع خطة الحل :

الاستراتيجية المناسبة في حل هذه المشكلة هي : البحث عن نمط . ولكن قبل ذلك نحتاج إلى الاستعانة بنوعين من الاستراتيجيات المساعدة ( هما : التمثيل بالرسم ثم عمل جدول ) ، كما يلي :

·      نمثل بالرسم بعض المضلعات ( المثلث ، الرباعي ، الخماسي ، السداسي ) :

3-تنفيذ الخطة :

·      نكون جدول بهذه البيانات :

·      نبحث عن نمط ، نتأمل قليلاً ، سنجد أن :

مجموع قياسات الزوايا الداخلية للمضلع = ( عدد الأضلاع – 2 ) × 180

إذاً في حالة المضلع المكون من 20 ضلعاً :

مجموع قياسات الزوايا الداخلية للمضلع = ( 20– 2 ) × 180 = 3240 ْ

4- مراجعة الحل :

       هل تمت الإجابة على السؤال ؟ نعم

3240 ْ = ( ن – 2 ) × 180

( ن - 2 ) = 18

ن = 20 ضلعاً .

مثال (2) :

أوجد  ت ¹⁰⁰⁰  ؟

الحل :

الاستراتيجية المناسبة لحل هذه المشكلة هي البحث عن نمط

الأمثلة الخاصة :

لنأخذ بعض الأمثلة الخاصة البسيطة ، مثلاً :

ت¹ = ت

ت²= -1

ت³ = - ت

ت ⁴ = 1

ت⁵ = ت

ت⁶ = -1

ت⁷= - ت

اكتشاف النمط :

من استعراض الأمثلة السابقة نكتشف النمط ، حيث نلاحظ أنه عندما يكون الأس زوجيا فأن الناتج يكون إما 1 أو -1 ، ويكون الناتج 1 إذا كان الأس عند قسمته على 2 زوجياً أيضاً . بينما يكون الناتج -1 عندما يكون الأس زوجي وعند قسمته على 2 يصبح عدداً فردياً .

أما عندما يكون الأس فردياً فإن الناتج يكون إما ت أو - ت ، ويكون الناتج ت إذا كان ( الأس – 1 ) عند قسمته على 2 يكون زوجياً بينما يكون الناتج - ت إذا كان قسمة ( الأس-1 ) على 2 ينتج عدداً فردياً .

التعميم :

ومنه نستطيع أن إيجاد المطلوب ، وهو :

ت ¹⁰⁰⁰ = - 1 لأن الأس زوجي وقسمته على 2 تساوي 500 ( فردي )

مثال 3 :

ما العلاقة بين عدد رؤوس وأوجه وأحرف المجسم المضلع ؟

الحل :

يمكن حل هذه المسألة عن طريق عمل جدول يمثل هذه المتغيرات لعدد من المجسمات المضلعة ، كما يلي:

إذا تأملنا الجدول السابق يمكن أن نستنتج ما يعرف بقاعدة أولر ونصها :

عدد أحرف المجسم المضلع = عدد أوجهه  +  عدد رؤوسه  -  2

مثال4 :

ما مجموع معاملات ( س + 1 )³¹ ؟

الحل :

يمكن تبسيط هذه المسألة عن طريق فحص حالات خاصة وبسيطة والبحث عن نمط ، كما يتضح ذلك من خلال الجدول التالي :

هل يمكن أن تكتشف النمط ؟

الآن : ما مجموع معاملات ( س + 1 )³¹ ؟

مثال5 : حضر ستة أشخاص في حفلة وأراد كل فرد أن يصافح الحاضرين مرة واحدة فقط .فكم عدد مرات التصافح التي تمت في هذه الحفلة ؟

الحل :

1-فهم المسألة :

المعطيات : عدد المتصافحين = 100 شخص

              عدد المصافحات بين كل شخصين = 1

المطلوب : العدد الكلي للمصافحات

2-وضع خطة للحل :

يقوم الطلبة بتمثيل الموقف عمليا على أن يقوم احد الطلاب بعد المصافحات التي تتم .

3-تنفيذ الخطة :

سوف يجد الطلبة أن وجود شخص واحد يعني عدم وجود أي مصافحة .

ثم يقوم الطلاب بتمثيل الموقف في الحالات التالية :

·      في حالة وجود شخصين فإن عدد المصافحات = مصافحة واحدة

·      في حالة وجود ثلاثة أشخاص فإن عدد المصافحات = 3 مصافحات

·      في حالة وجود أربعة أشخاص فإن عدد المصافحات = 6 مصافحات

·      في حالة وجود خمسة أشخاص فإن عدد المصافحات = 10 مصافحات

يوقف المعلم التمثيل عند هذا الحد ويطلب من الطلاب استنباط العلاقة بين عدد الأشخاص وعدد المصافحات .

·      يجيب أحد الطلاب انه عندما يكون لدينا ثلاثة أشخاص فإن :

عدد المصافحات = مجموع الأعداد من واحد إلى اثنين 1+2 .

·      ويجيب آخر أنه إذا كان لدينا أربعة أشخاص فإن :

عدد المصافحات = مجموع الأعداد من واحد إلى ثلاثة 1+2+3

·      ويجيب طالب ثالث أنه إذا كان لدينا خمسة أشخاص فإن

عدد المصافحات = مجموع الأعداد من واحد إلى أربعة 1+2+3+4

لأن الشخص الخامس سوف يصافح أربعة أشخاص فقط

يسأل المعلم : ما العلاقة إذا بين عدد الأشخاص وعدد المصافحات ؟

يجيب طالب أن العلاقة بين عدد الأشخاص وعدد المصافحات هي :

عدد الأشخاص × (عدد الأشخاص – 1 ) ÷ 2 = 5×4÷2=10

والآن : لو كان لدينا عشرين شخص كم يكون عدد المصافحات ؟

سوف يجيب احد الطلاب أن عدد المصافحات سيكون :

مجموع الأعداد من 1 إلى 19= عدد الأشخاص × (عدد الأشخاص – 1 ) ÷ 2 = 20×19÷2=190

إذاً كان لدينا 100 شخص فإن عدد المصافحات = 100× 99 ÷ 2 = 4950

4- مراجعة الحل :

       هل كان المطلوب هو إيجاد عدد المصافحات ؟ نعم .

       هل يبدو الجواب معقولاً ؟ نعم .

طريقة أخرى للحل :

الاستراتيجية المستخدمة في هذه الطريقة هي : البحث عن نمط . ولكن قبل ذلك نحتاج إلى الاستعانة بنوعين من الاستراتيجيات المساعدة ( هما : التمثيل بالرسم ثم عمل جدول ) ، كما يلي :

لنسمي الأشخاص  أ ، ب ، جـ ، د ، هـ ، و  . كل شخص يصافح الحاضرين دون تكرار .

سوف نستخدم الدائرة التالية كتمثيل للمشكلة ؛ حيث تُعبر النقاط عن الأفراد ، وتمثل الخطوط بين النقاط عن عدد مرات التصافح بين الأفراد وتمثل الأسهم اتجاه المصافحات .

ويمكن اعتبار أن عدد مرات التصافح  = عدد الأسهم  .

وبعد مناقشة الرسم التوضيحي مع التلاميذ يمكن كتابة عدد مرات التصافح في الجدول التالي :

ومنه نجد أن :

عدد مرات التصافح  = 5 + 4 + 3 + 2 + 1 = 15

ويمكن استخدام هذا التمرين كتمهيد لموضوع التوافيق الذي يدرسه التلميذ في الثانوية ، وبالتالي يمكن حله كما يلي  :

إذا كان  ن  يمثل عدد الأفراد فإن  :

                              ن             ن ( ن- 1 )                

   عدد مرات التصافح =   --     =   ----------   

                              2                  2

                                  6              6  ×  5             30

 إذا عدد مرات التصافح  =    --     =  ---------  =  ------ =  15

                                  2                  2                  2

مثال 6 :

إذا كانت : د(س) = أس² + ب س + جـ .

 هـ (س) = جـ س² + ب س + أ .

فما العلاقة بين جذور د(س) و هـ (س) ؟

الحل :

قد لا تتضح العلاقة بين جذور د(س) و هـ (س) عن طريق الحل بواسطة القانون ، ولكن الاستراتيجية المقترحة لحل هذه المشكلة هي تبسيط المسألة عن طريق فحص حالات خاصة ، فقد تكون مفتاحاً للحل. فعندما نختار حالات خاصة من المعادلات القابلة للتحليل ونحسب جذورها فإن العلاقة ستتضح .

أنظر الجدول التالي واكتشف العلاقة :

هل اكتشفت العلاقة ؟

تأكد من صحة الحل الذي توصلت إليه ؟

مثال 7 :

أوجد الحد النوني وعدد المكعبات المستخدمة في بناء شكل عدد حدوده ن ، بُني بالشكل التالي :

الحل :

الاستراتيجية المناسبة لحل هذه المشكلة هي استراتيجية البحث عن نمط .

حدود هذه المتسلسلة تأخذ الأشكال التالية:

ومنه يتضح أن عدد المكعبات في كل حد منها هو مجموع الأعداد الطبيعية لرتبة ذلك الحد .

الآن نوجد مجموع المتسلسلة للحد النوني كما يلي :

 (4) استراتيجية تبسيط المشكلة :

  problem Simplification

وذلك بتحويل المسألة من معقدة إلى بسيطة ، فنقوم بحل مسألة أبسط من المسألة المطلوبة ، ومن ثم تعميم الحل ليمتد إلى حل المسألة المطلوبة .

خطواتها : يقوم التلميذ بـ :

1)  تبسيط المسألة بأحد طرق تبسيط المشكلة ( سيأتي الحديث عنها ) .

2)  حل المسألة الأبسط .

3)  تعميم الحل ليمتد إلى المسالة المطلوبة .

ولتبسيط المشكلة عدة طرق ، نذكر منها :

               أ‌-          تبسيط الأرقام المتضمنة في المشكلة من كبيرة إلى صغيرة ، أو من معقدة إلى بسيطة .

    ب‌-  تجزيء المشكلة والبحث عن حلول جزئية ، وبطريقة ما نتمكن من تركيب هذه الحلول الجزئية لتكون الحل العام للمشكلة الأصلية .

    ت‌-  تثبيت أو إضعاف أو حذف بعض الشروط أو تقليل عدد المتغيرات إن أمكن ذلك ، ويمكن التعبير عن ذلك بعبارة بوليا : خذ شرطاً واحداً ثم أضف شرطاً آخر . فكرة حل المشكلة الجديدة يمكن أن تقودنا إلى الحل النهائي للمشكلة الأصلية .

            ث‌-       الربط بمشكلة مشابهة نعرف فكرة حلها .

    ج‌-   كما أن فحص حالات خاصة من المشكلة ، ومن ثم اكتشاف الحل أو النمط (استراتيجية البحث عن نمط ) أحد أنواع تبسيط المشكلة .

    ح‌-  الاستفادة من التماثل الموجود في المشكلة : فكثير من المشكلات الرياضية يمكن حلها عن طريق الاستفادة من التماثل الداخلي في بنية المشكلة . وغالباً ما يكون تتبع هذا التماثل في المشكلة قد ينمي في الطالب القدرة على إهمال المعلومات التي ليس لها علاقة والتركيز على المعلومات أو العناصر ذات العلاقة . بالإضافة إلى ذلك فإن فكرة التماثل موجودة في كثير من فروع الرياضيات وبالذات في الهندسة حيث تدرس موضوع مستقل .

متى تستخدم : هذه الاستراتيجية مفيدة :

1)  عندما تكمن صعوبة المسألة في أرقامها المعقدة ، فإننا نستخدم الطريقة (أ).

2) وعندما تكون المشكلة مركبة من مشكلات جزئية يمكن تجزئتها عن بعضها فإننا في هذه الحالة نستخدم الطريقة (ب) .

3)  أما إذا كانت شروط المشكلة كثيرة فعندئذ يمكن أن نستخدم الطريقة (ت).

4) وإذا كانت فكرة المشكلة مشابهة لفكرة مشكلة أخرى نعرف طريقة حلها ، فإننا نستخدم الطريقة (ث) .

5) وعندما يكون المطلوب هو حل عام للمشكلة ( قانون ما ) وبدراسة حالات خاصة منها يمكن أن تكون مفتاحاً لاكتشاف الحل ( النمط ) ، ففي هذه الحالة نستخدم الطريقة (ج).

6) وعندما يكون هناك تماثل في المشكلة فيمكن حلها عن طريق الاستفادة من التماثل الداخلي في بنية المشكلة ، ففي هذه الحالة نستخدم الطريقة (ح).

مثال1 :

أوجد مجموع الأعداد الصحيحة من 1 إلى 200 والتي ليست من مضاعفات العدد 4 أو العدد 9 ؟

الحل :

الاستراتيجية المقترحة لحل هذه المشكلة هي تبسيط المسألة عن طريق تجزيء المشكلة والبحث عن حلول جزئية ، حيث يمكن تجزيء هذه المشكلة إلى ثلاث مشكلات جزئية ، هي :

1)  أوجد مجموع الأعداد الصحيحة من 1-200 ؟ ( = 200 × 201 ÷ 2 )

2)  أوجد مجموع مضاعفات العدد 4 إلى 200 ؟ ( = 4 × 50 × 51 ÷ 2 )

3)  أوجد مجموع مضاعفات العدد 9 إلى 200 ؟ ( = 9 × 22 × 23 ÷ 2 )

ثم يكون الحل العام للمشكلة الأصلية = الحل الأول – الحل الثاني – الحل الثالث .

مثال 2 :

أ ب جـ د شبه منحرف ، أطواله كما هو موضحاً في الرسم ، والمطلوب: احسب مساحة الشكل ؟

الحل :

يمكن استخدام استراتيجية تبسيط المسألة عن طريق تجزيئها إلى مشكلات جزئية والبحث عن حلول جزئية ، فنقوم بعمل الإنشاءات التالية :

من النقطة ب نرسم موازٍ لـ جـ د يتقاطع مع أد في هـ

ومن النقطة جـ نرسم موازٍ لـ أب سيتقاطع مع أد في النقطة السابقة هـ

ومن الواضح أن هذه المثلثات الثلاثة متطابقة ، وعليه فإن :

مساحة شبه المنحرف = 3 × مساحة مثلث واحد .

ومن الواضح أيضاً أن هذه المثلثات فيثاغورثية ، لأن :

مما يعني أن المثلثات قائمة ، وهذه الزاوية هي المحصورة بين الضلعين اللذين طولاهما : 8 ، 6 .

إذاً : مساحة المثلث الواحد هي =  × 8 × 6 = 24

ومنه نجد أن : مساحة شبه المنحرف = 3 × 24 = 72

طريقة أخرى للحل :

لنعمل الإنشاءات التالية :

نسقط عمودين من النقطتين ب وَ جـ على القاعدة أد ، كما يظهر في الشكل التالي :

فيصبح لدينا ثلاثة أشكال هي :

المستطيل روجـ ب ، والمثلثين : أرب ، ودجـ .

بتطبيق قاعدة فيثاغورس على المثلثين القائمين أ ر ب ، د وجـ نجد أن :

بتعويض المعادلة (2) في (1) نجد :

وبتعويض قيمة x في المعادلة (2) نجد :

ومنه نجد أن مساحة شبه المنحرف ، هي :

مثال3 :

أوجد طول الضلع أجـ في الشكل التالي ، إذا علمت أن :

الشكل أ ب جـ م مستطيل ، وطول أم = 5 سم ، وطول أد = 1 سم ، م مركز الدائرة ؟

الحل :

الاستراتيجية المقترحة لحل هذه المشكلة هي الاستفادة من التماثل الداخلي في بنية المشكلة .

                 فطول أجـ = طول م ب  ( قطرين في مستطيل واحد )

                 وطول م ب = طول أم + طول أد ( لأنه نصف قطر في الدائرة )

             إذاً : طول م ب = 5 + 1 = 6 سم

مثال3 :

أوجد الحد النوني ومجموع مكعبات بناء المجسم التالي:

الحل :

الاستراتيجية المناسبة لحل المشكلة السابقة هي استراتيجية تبسيط المشكلة بالاستفادة من التماثل ، ويتضح ذلك في الشكل التالي :

ويتضح أن الشكل مؤلف من عدة أجزاء متماثلة : هل تعرف كم عددها ؟

سوف يتم توضيح هذه الأجزاء ، في الرسم التالي :

هذه الأجزاء الأربعة عبارة عن النصف العلوي من الشكل ، ويمكن مشاهدة الأجزاء التي تكون النصف السفلي من الشكل ، كما في الرسم التالي :

من خلال الرسومات السابقة : هل تستطيع أيجاد مجموع المتسلسلة ؟ كيف؟

يمكن ملاحظة أن الشكل مؤلف من ثمان متسلسلات من نوع واحد ، وهي المتسلسلة التي حدها النوني هو :

وبالتالي فإن مجموع الحد النوني للمتسلسلة السابقة هو :

إذا عدد المكعبات التي نحتاجها ( 280 ) مكعباً .

(5) استراتيجية العمل للخلف (أو البدء من النهاية) :

  Work backwards:

ويتم فيها إتباع الطريقة التحليلية في التفكير ، وذلك خلافاً لباقي الاستراتيجيات حيث يتم البدء بالمطلوب بدلاً من المعطى ، فاستخدام هذه الإستراتيجية يتضمن البدء من الخلف ، أي من ناتج المسألة باتجاه مقدمتها . وهذه الطريقة قد تساعد على التخلص من الاحتمالات الخاطئة والسير نحو الحل الصحيح .

خطواتها : يقوم التلميذ بـ :

1)  البدء من المطلوب .

2)  البحث عما يحققه المطلوب والاستمرار في ذلك وصولاً إلى الهدف .

متى تستخدم : هذه الاستراتيجية مفيدة :

عندما تتضمن المشكلة سلسلة من الحسابات المتتالية لعدد ما ويعطى الناتج النهائي لهذه الحسابات، والمطلوب إيجاد قيمة عدد في أحد الحسابات التي في بداية المشكلة والتي قد يصعب حسابها إذا سرنا من المعطيات. وعادة يواجه التلميذ - في هذا النوع من المشكلات - صعوبة في تكوين المعادلات الجبرية أو في استخدام استراتيجيات العمل للأمام بشكل عام .

مثال1 :

سيارة مملؤة بطيخ يريد صاحبها عبور سبعة بوابات على كل منها حارس يريد نصف ما معه من البطيخ . في النهاية بقي معه بطيخة واحدة ؟ كم كان معه قبل عبور البوابات السبع ؟

الحل :

1-فهم المسألة :

   المعطيات : صاحب السيارة سيعبر 7 بوابات .

               على كل بوابة حارس يأخذ نصف البطيخ .

               بقي معه بطيخة واحدة .

       المطلوب : كم كان معه قبل عبور البوابات السبع ؟

2-وضع خطة الحل :

الاستراتيجية المناسبة لحل هذه المشكلة هي البدء من الخلف لأنها سلسلة من الحسابات والمطلوب أحد الحسابات الواردة في بداية المسألة (كم كان معه قبل عبور البوابات السبع ؟ ) .

3-تنفيذ الخطة :

قبل استخدام استراتيجية البدء من الخلف ؛ يمكن الاستعانة بجدول (كاستراتيجية مساعدة ) :

فيكون معه 128 بطيخة قبل عبور البوابات السبع .

3-مراجعة الحل :

للتأكد من صحة حل هذا المثال ، نبدأ بمقدمة المشكلة حتى نصل إلى نهايتها كما يلي : 

مما يدل على صحة الحل .

مثال 2 :

نام ثلاثة أشخاص تحت شجرة وعندهم صندوق مشمش ، استيقظ الأول وقسّم حبات المشمش ثلاثة أقسام بالتساوي وبقيت حبة واحدة رماها للقرد ، وأكل قسمته ونام . ثم استيقظ الثاني وفعل مثل الأول ونام . ثم استيقظ الثالث وفعل مثل الثاني ونام . ثم استيقظ الجميع وقسموا الباقي بينهم بالتساوي وبقيت واحدة رموها للقرد ، وأكل كل قسمته . والسؤال : كم حبة أكلها الأول ؟

الحل :

الاستراتيجية المناسبة لحل هذه المشكلة هي البدء من الخلف لأنها سلسلة من الحسابات والمطلوب أحد الحسابات الواردة في بداية المسألة.

نفرض أن : عدد الحبات التي بقيت في المرة الأخيرة  .

   ما أكله القرد + ما قسم بين الثلاثة = x+1

وهذا يعني أن x يجب أن تكون من مضاعفات العدد 3 .

الآن يمكن تطبيق استراتيجيتي بناء معادلة رياضية والبدء من الخلف بالاستعانة بجدول ( كاستراتيجية مساعدة ) كما يلي :

الآن نبحث عن قيمة لـ x  تحقق الشرطين التاليين :

1.  من مضاعفات العدد 3 .

2.  بعد التعويض وإجراء الحسابات تجعل قيمة الكسر السابق :

 عدداً صحيحاً.

ولايجاد هذه القيمة نستخدم استخدام استراتيجية المحاولة والخطأ المنظمة ، والاستعانة بجدول (كاستراتيجية مساعدة) ، كما يلي :

ومنه نجد أن عدد حبات المشمش كانت 79 حبة ، فلما أفاق الأول قسمها إلى (26+26+26) وبقيت واحدة رموها للقرد .

التأكد من صحة الحل :

يمكن التأكد من صحة الحل من خلال الجدول التالي :

(6) استراتيجية التفكير الإبداعي

  The Creative Thinking:

والذي يعرف بأنه : " نشاط عقلي مركب وهادف توجهه رغبة مركبة في البحث عن حلول أو التوصل إلى أنواع أصلية لم تكن معروفة سابقاً ، ويتميز بالشمولية والتعقيد لأنه نطوي على عناصر معرفية وانفعالية وأخلاقية متداخلة تشكل حالية ذهنية فريدة".

وفيها ينظر إلى المشكلة بطرق جديدة ومخترعة ، ونستخدم فيها التخيل والإبداع ونوظف كل الوسائل الممكنة ، وتتطلب منا مرونة واستمرارية في التفكير ، فيستمر المصباح مضيئاً وفي النهاية سنصل إلى الحل .

متى تستخدم : هذه الاستراتيجية مفيدة :

عندما تعجز باقي الاستراتيجيات عن حل المشكلة ، وأحيانا قد تكون أحد الحلول التي تفكر فيها في حل مشكلة ما رغم إمكانية حلها بطريقة أخرى .

مثال 1 :

أوجد مجموع الأعداد الـ 100 الأولى ؟

الحل :

يمكن حل هذه المشكلة بأكثر من استراتيجية ، ومن ذلك تطبيق قانون مجموع الأعداد الطبيعية لإيجاد الناتج مباشرة .

لكن الذي يعنينا منها في هذه الاستراتيجية التفكير الإبداعي التالي في حل هذه المشكلة :

سأل المعلم تلاميذه : عن هذا السؤال ؟

فأجاب أحد التلاميذ بسرعة ، الجواب = 5050 .

فكيف أستطاع التلميذ حساب المجموع بسرعة. لقد فكر التلميذ في حل هذه المسألة بالشكل التالي :

رتب الأعداد مرتين أحدهما تصاعدياً والأخرى تنازلياً ، ثم جمع الأعداد في كل عمود ليجد أن المجموع دائماً = 101 ، وذلك كما يلي :

وحيث أن عدد هذه المجاميع هو 100 ، فيصبح مجموع هذه الأعداد

=  100 × 101 = 10100

ولكن هذا المجموع هو مجموع الأعداد مرتين ، فيصبح المجموع المطلوب هو نصف هذا المجموع ، أي = 10100 ÷ 2 = 5050

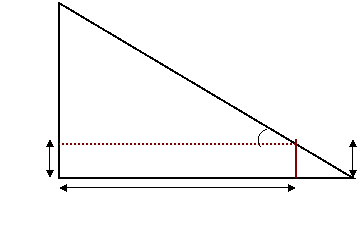
مثال2 :

لدينا ساريتي علم طول كل واحدة منها 100 قدم ، ويتدلى بينهما حبل طوله 150 قدم ( يبدأ من قمة السارية الأولى وينتهي بقمة السارية الثانية ) ، وكان أكثر أجزاء الحبل انخفاضاً يرتفع عن سطح الأرض مسافة قدرها 25 قدماً (أنظر الرسم ) . والمطلوب : أحسب المسافة بين الساريتين ؟

الحل :

استراتيجية التفكير الإبداعي هي المناسبة في حل هذه المشكلة ، حيث أن الطالب سيلاحظ أن : ارتفاع السارية = 100 قدم .

طول الحبل = 150 قدم .

فإذا طويناه إلى نصفين متساويين يصبح طول نصف الحبل = 75 قدم .

وارتفاع أكثر أجزاء الحبل انخفاضاً عن سطح الأرض مسافة قدرها 25 قدم .

فمنه يظهر أن الساريتين متلاصقتين ( أي كأنهما سارية واحدة ) .

فتصبح المسافة بينهما = صفر .

مثال 3 :

سلم من حبل متدلي على جانب سفينة ، مكون من 15 درجة ، كل درجة ارتفاعها 30 سم ، إذا كان الماء يصل إلى منتصف الدرجة السفلى ، وكان معدل ارتفاع المد 5سم/س ، فمتى يغطي الماء الدرجات الست الأولى ؟

الحل :

لن يغطي الماء هذه الدرجات لأن السلم يرتفع مع ارتفاع السفينة وهي تطفو على الماء .