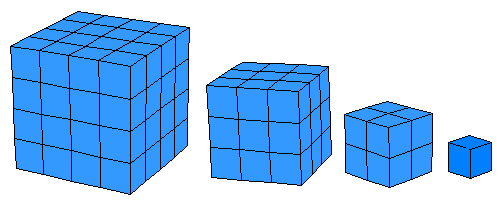الأعداد المكعبة

لتكن لدينا متتابعة الأعداد التالية : 1 ، 8 ، 27 ، 64 ، ......

يمكن أن نستنتج الحد النوني لهذه المتتابعة باستخدام المكعبات المتداخلة ، وذلك كما يلي :

• نأخذ مكعبات بعدد هذه الأعداد .
• نقوم بتركيب المكعبات الخاصة بكل عدد على أن يكون الشكل الناتج على صورة مكعب . سنتوصل إلى الأشكال التالية:

• نحدد أبعاد كل مكعب . سنجد أن :

1=1×1×1      8=2×2×2      27=3×3×3     64=4×4×4

وعليه فإنه من الواضح أن حدود هذه المتتابعة هي مكعبات الأعداد : 1 ، 2 ، 3 ، 4 ، .... على الترتيب . حيث :

 الآن وبعد أن تعرَّفنا على الحد النوني لهذه المتتابعة لنطرح السؤال التالي:

مثال 1 :

لتكن لدينا متتابعة الأعداد التالية : 1 ، 8 ، 27 ، 64 ، ...... . أوجد مجموع هذه المتتابعة ؟

الحل :

أولاً :  باستخدام اليدويات

المطلوب هو إيجاد مجموع الأعداد المكعبة أو ما يرمز له بالرمز :

نقوم بتمثيل مجموع الأعداد السابقة باستخدام المكعبات المتداخلة كما يلي :

وهكذا نستنتج أن مجموع ن حد من حدود هذه المتتابعة هو مربع طول ضلعه (1 + 2 + 3 + 4 + .... + ن ) وهو ما نعرفه سابقاً بأنه مجموع الأعداد الطبيعية ، وعليه فإن مجموع هذه الحدود هو مساحة هذا المربع ، أي :

ومنه نحصل على مجموع الأعداد المكعبة وهو :

ثانياً :  رياضياً باستخدام طريقة الفروق :

لإيجاد مجموع الأعداد المكعبة باستخدام طريقة الفروق نعمل الجدول التالي :

وبما أن الفرق الثالث ثابت فإن معادلة المجموع من الدرجة الرابعة وتكتب معادلتها بالصورة :

وبالتعويض عن قيمة n في هذه المعادلة بالأعداد :1 ، 2 ، 3 ، 4 ، 5 على التوالي نحصل على المعادلات الخمس التالية :       

وبمقارنة هذه المعادلات بالفروق السابقة نحصل على قيم المعاملات في المعادلة السابقة ، كما يلي :   

وبتعويض هذه القيم في المعادلة السابقة نحصل على التالي :

    وهو قانون مجموع الأعداد المكعبة .