قطع دينز

الفئة المستهدفة:

طلاب المرحلة الابتدائية والمتوسطة

هدف البرمجية

تهدف البرمجية إلى تنمية عدد من المهارة الحسابية والجبرية لدى الطالب ومنها:

واجهة البرمجية واستخدامها:

هذا البرنامج سهل جدًّا و ذو استخدام محسوس ، كما ترى من الشكل أدنا , القطع الملوّنة على اليسار هي المكعبات التي يمكن أن تضغط عليها لعمل الأشكال الجديدة بطريقة سحريّة ، تستطيع التأشير على هذه القطع ثم سحبها إلى منطقة العمل في الوسط . وقد صنعت منطقة العمل بشكل شبكة مربعة لتسهيل تحريك القطع وتجميعها ، وليس هناك حدّ لعدد القطع التي يمكن سحبها وتحريكها  تقريبا . القطع الثّلاثة المستخدمة من قبل هذا البرنامج هي القطع العاديّة المستخدمة في المكعبات المجسمة ما عدا المكعب الكبير .

  وهنا وصف قصير للأشكال الثلاثة المستعملة في هذا البرنامج

  دعنا الآن نصف باقي  الأدوات الأخرى على اليسار و الأعلى وهي تغير العمل كلما ضغطت على زر الفارة.  ويصف الجدول التّالي كلّ الوظائف المتاحة :

الوصف	رمز الأيقونة
هذا هو المؤشّر العاديّ , يضع البرنامج في الأسلوب العاديّ الذي يمكن أن تعمل فيه , وتختار وتسحب القطع .
بعد الضّغط على هذه الأيقونة يتغير عمل المؤشر إلى عملية تغيير وضع القطع الزرقاء  من الوضع الأفقي إلى الرأسي والعكس وللرجوع للوضع العادي اضغط المؤشر مرة أخرى .
هذا الشاكوش يكسر أيّ من القطع الكبيرة إلى الحجم الأصغر. انتق الشاكوش و اضغط على قطعة 100 لكسرها إلى 10 قضبان  وهكذا .. وللرجوع للوضع العادي اضغط المؤشر مرة أخرى .
يعمل الصمغ عكس ما يعمله الشاكوش
يمكن أن تضغط على هذا الحبل اللطيف لتجمع معًا عدد كبير من القطع . بعد الضّغط على الحبل , ارسم بالمؤشر حبلا يحيط الأشكال التي تريد تجميعها فتصبح شكلا واحدا تستطيع تحريكها معا أو تكسيرها أو تجميعها أو رميها في سلة المهملات وطريقة الرجوع للوضع العادي كما سبق.
هذه السلة تصلح لرمي أي قطعة أو مجموعة لا تحتاجها في ساحة العمل.

  ويظهر الجدول التالي القائمة الكاملة من خلفيات العمل المتاحة في هذا البرنامج و العمليات المتاحة لكل منها :

بعض استخدامات

(1) عملية العد :

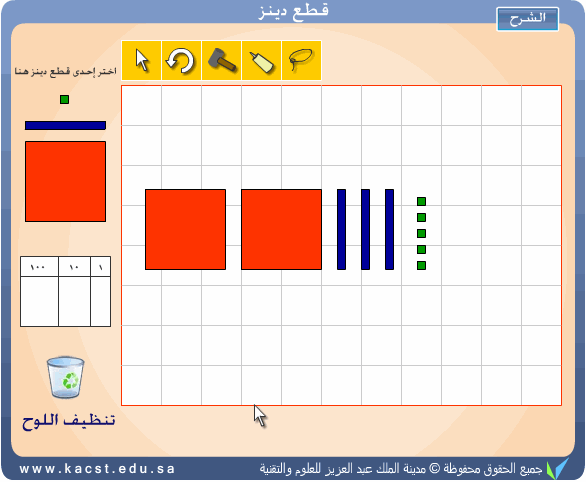
يستطيع المتعلم من خلال هذا البرنامج تعلم تمثيل العدد عندما يقوم بإخراج عدد من القطع إلى ساحة العمل ويحصيها فمثلاً العدد 235 يمكن تمثيله بالصورة :

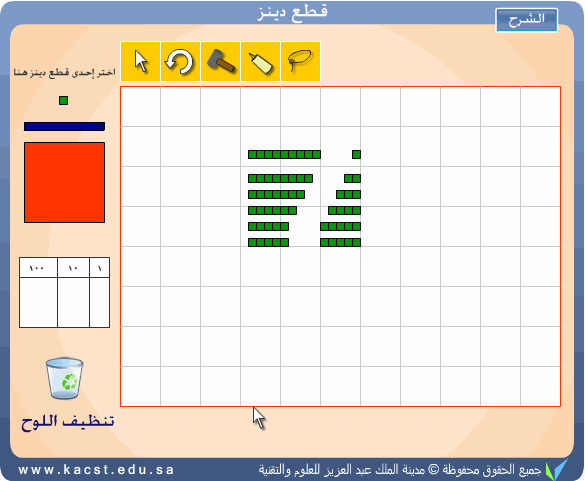
 (2) - مكونات العدد عشرة :

يمكن تكوين شريط من عشرة وحدات صغيرة ومن ثم تجزئته عدة مرات مما يسهل دراسة مكونات العدد عشرة وبشكل اسهل يمكن اخذ عمود وكسره بالشاكوش فيعطينا عشرة وحدات صغيرة.

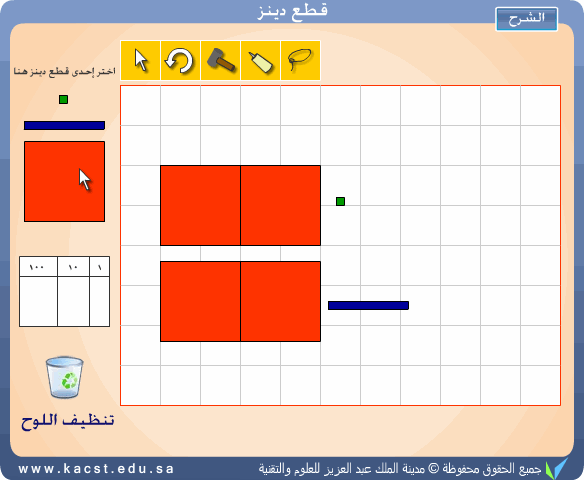
(3) - المقارنة بين الأعداد الصحيحة :

يمكن إجراء المقارنة بين أي عددين باستخدام هذه المكعبات بكل سهولة وذلك من خلال تمثيل العددين على اللوحة ومقارنة القطع الكبرى ثم الأصغر وهكذا .والمثال التالي يوضح مقارنة العددين 120 ، 201 حيث يلاحظ الطالب أن 120 أصغر من 201

   (4) تمييز القيمة المكانية للرقم ( دراسة المنازل ) 

من خلال هذا البرنامج نستطيع تقديم القيمة المكانية للأرقام في كل عدد من خلال دراسة الآحاد والعشرات والمئات أو من خلال دراسة الآحاد وأجزاء العشرة وأجزاء المائة من خلال تمثيلها حسب الخلفية المناسبة. كما هو موضح في المثالين التاليين :

تمثيل العدد 248   

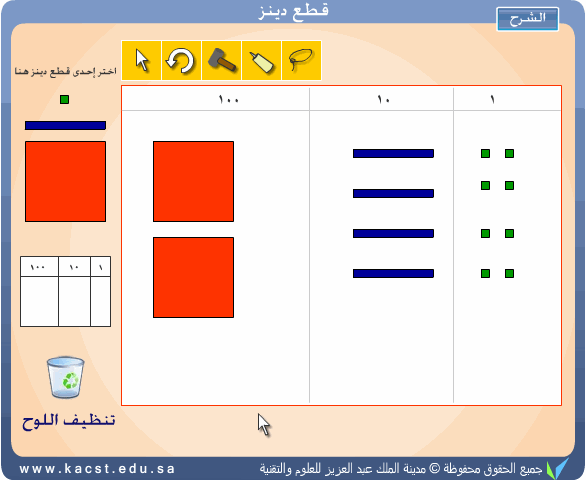
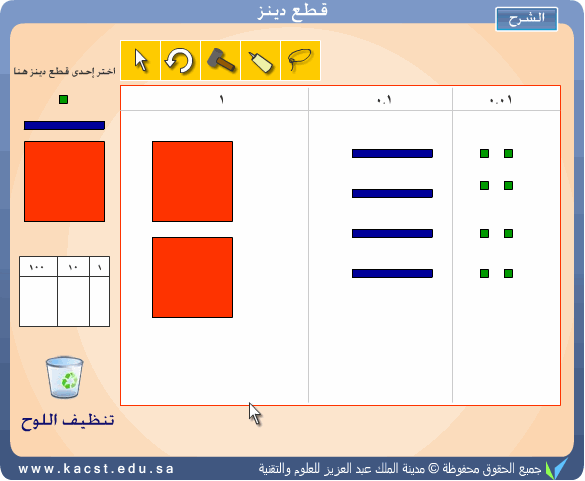
 تمثيل العدد  2.48

(5) - إتمام عمليات الجمع مع الحمل أو بدونه :

 تتلخص عملية الجمع بتمثيل العدد الأول ( بوضع كل وحدة تحت العمود المناسب لها ) ثم تمثيل العدد الثاني على نفس الشكل وبعد ذلك يتم تجميع القطع الصغيرة إلى القطع الأكبر منها وتحويلها إلى العمود المناسب فيكون ما يوجد على اللوحة هو المجموع .ويفضل أن تكون خلفية العمل هي [ 1 ، 10 ، 100 ] أو [ 0.01  ، 0.1  ، 1 ].

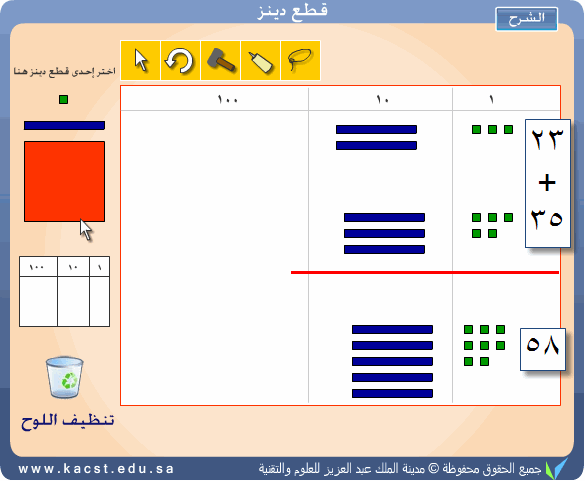
ونستطيع تمثيل عملية الجمع كما هو موضح بكل بساطة باستخدام مكعبات البرنامج :

 23 +  35 = 58

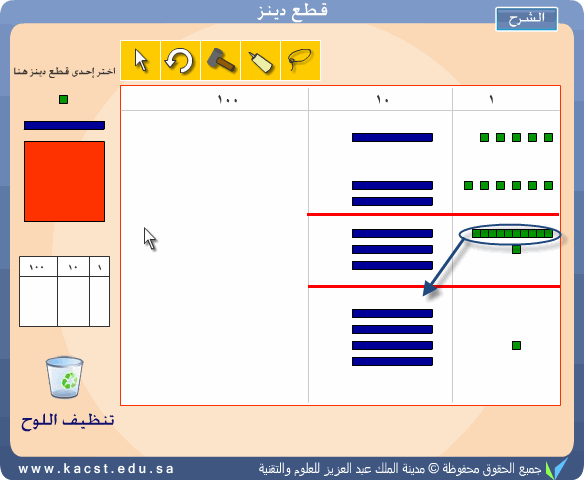
  أو يمكن إجراء عملية الجمع مع حمل وتطبيق نظام المقايضة كل 10 وحدات بوحدة اكبر منها مباشرة كما يوضح ذلك المثال التالي   15 + 26 = 41 

 (6) - إتمام عمليات الطرح بالاستلاف أو بدونه :

تتلخص هذه العملية بتمثيل العدد المطروح منه ثم القيام بسحب (طرح) العدد المطروح من اللوحة ورميه في سلة المهملات (قد نحتاج إلى تكسير بعض القطع الكبيرة لإتمام العملية) فيكون ما يوجد على اللوحة هو الناتج. ويفضل أن تكون خلفية العمل هي [ 1 ، 10 ، 100 ] أو [ 0.01  ، 0.1  ، 1 ]. وهنا يمكن أن يظهر مفهوم الطرح أو (الأخذ) بوضوح من خلال تطبيق العملية باستخدام البرنامج

والمثال التالي يوضح العملية  234-121 = 113

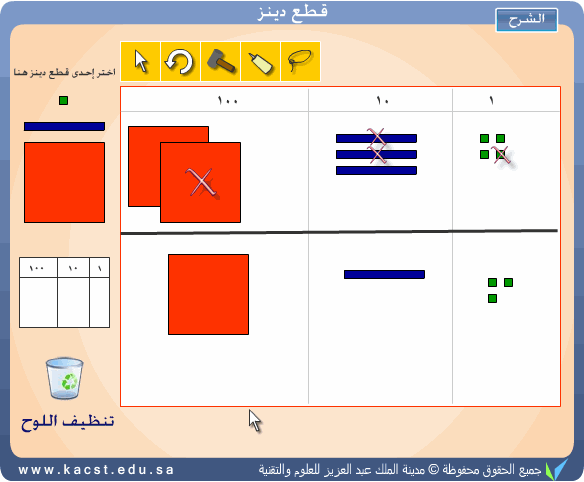
  ويمكن كذلك إجراء عملية الطرح بالاستلاف بشكل جميل وواضح كما يلي :

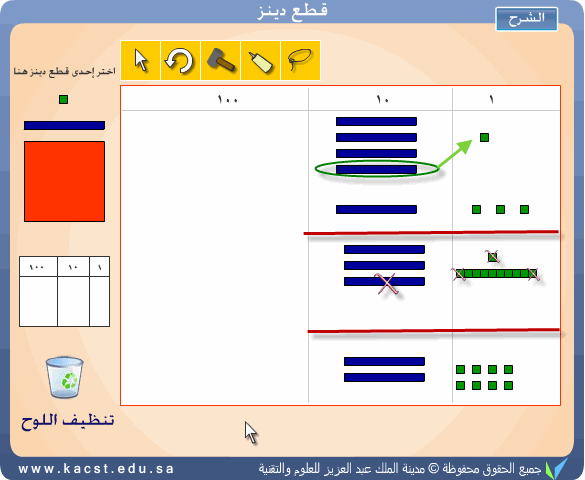
حيث نمثل المطروح منه على اللوح ثم نحاول حذف المطروح من المطروح منه ولكن لا يمكن ذلك وعليه نستلف عمود من العشرات ونكسره في منزلة الآحاد ليتصبح الآحاد 11 ثم نأخذ منها الآن  3  من الوحدات فيصبح لدينا الباقي في الآحاد 8 ونطرح العشرات بشكل عادي فيكون المتبقي لدينا بعد الطرح  28  .

  (7)- عملية الضرب :

 مع عملية الضرب تصبح العملية اكثر إمتاعا عندما يتخيل الطالب المنطقة الممثلة لعملية الضرب بمنطقة مستطيلة يكونها هو بنفسه ويظهر ذلك من خلال المثال التالي:

ما هو حاصل الضرب  7 × 12 ؟

في هذه العملية نستخدم الخلفية ( محور س ص )  ونحاول تمثيل المضروب اسفل المحور الأفقي والمضروب فيه يسار المحور الرأسي أو العكس ثم نحاول إكمال الشكل المستطيل الذي طولي ضلعيه هما 7 و 12 فيكون مجموع الوحدات داخل المحورين هو ناتج الضرب والذي يمثل هنا 7 قضبان و 14 وحدة صغيرة .

  7×12 = 7 قضبان + 14 وحدة = 70 + 14 = 84

 (8)- عملية القسمة :

توجد للقسمة ثلاث طرق  هي :

أولا : طريقة القياس

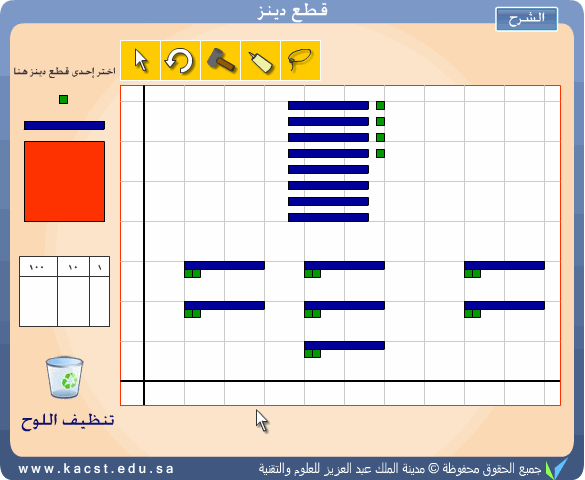
وتتمثل هذه الطريقة بتمثيل المقسوم كاملا على اللوحة ثم محاولة اخذ مجموعة عددها يساوي المقسوم عليه ( قد نحتاج إلى تكسير القطع الأكبر) وإبعادها جانبا مع التكرار حتى لا يبقى شيء من المقسوم ، ثم نقوم بعد المجموعات الناتجة من الأخذ كما في الشكل المقابل الذي يمثل 84÷ 7 = 12

 

ثانيا : طريقة ( العد) :

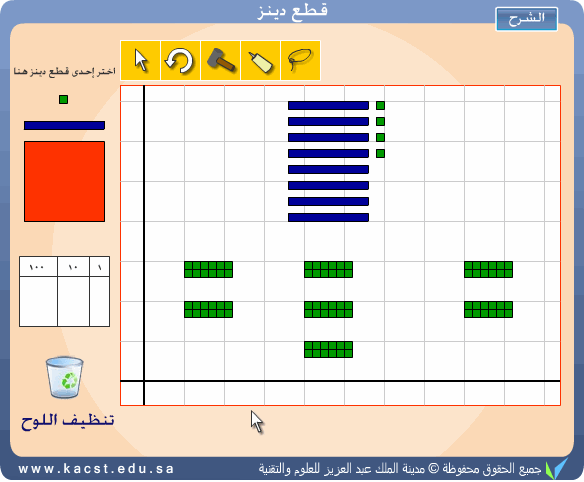
تتمثل هذه الطريقة في اخذ القطع واحدة واحدة ووضعها في مجموعات عددها يساوي المقسوم عليه ، حتى ينتهي المقسوم ثم بعد ذلك نقوم بعد الوحدات في كل مجموعة فيكون هو الناتج ، والمثال المقابل يمثل:

 84÷ 12 = 7

ثالثا : طريقة السقالة :

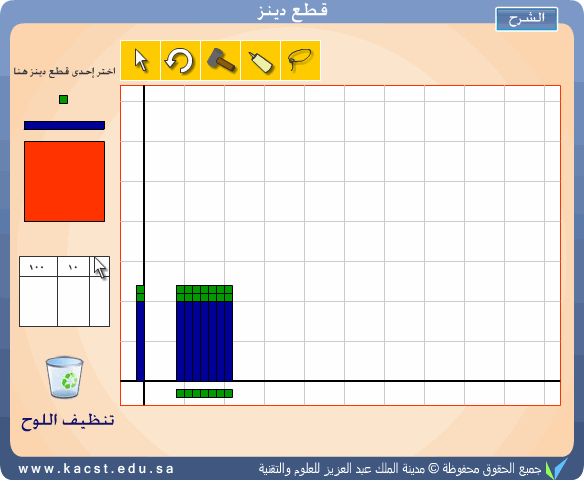
وتتمثل هذه الطريقة تمثيل المقسوم على اللوحة ومن ثم استخدام المحور الأفقي في تمثيل المقسوم عليه ومن ثم محاولة تكوين مستطيل من القطع التي تمثل المقسوم فقط بحيث تكون قاعدته هي المقسوم عليه وفي هذه الحالة يكون ناتج القسمة هو ارتفاع المستطيل. والمثال المقابل  يمثل 84÷ 7 = 12

  (9)- استخدام الأرقام العشرية:

يمكن أيضا تقديم عدة تمارين على الكسور العشرية والأعداد العشرية وقيمة المنازل حيث تمثل الطبقة الحمراء الوحدة 1 وتمثل العصا الزرقاء عشرها أو 0.1 وتمثل الوحدة الخضراء جزء المائة منها أو 0.01 ونستخدم لذلك الخلفية [1 ، 0.1 ، 0.01 ] ويمكن إجراء العمليات عليها كالجمع والطرح أو الضرب والقسمة على عدد صحيح كما سبق التعامل معه في الأعداد الصحيحة.

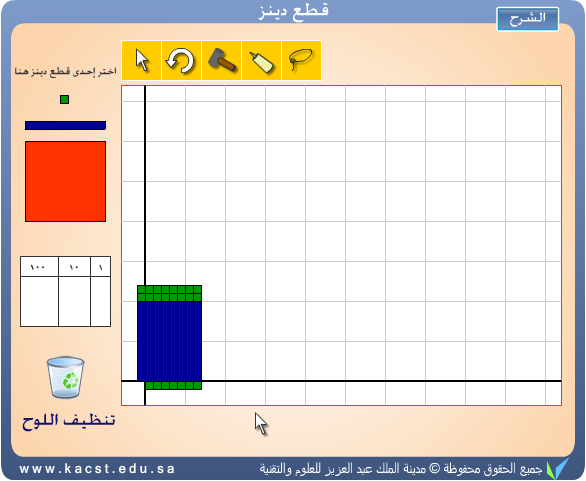
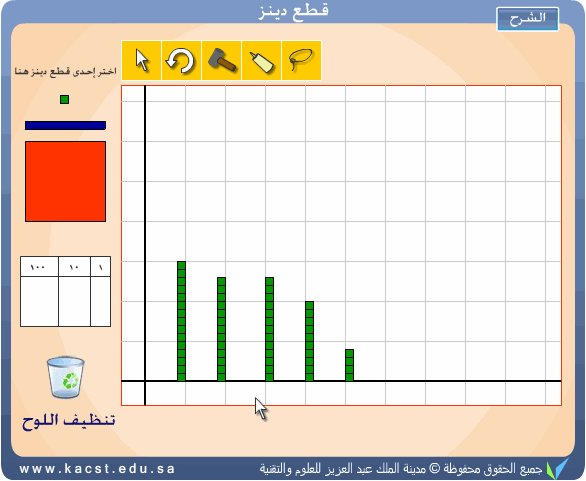
(10)- الرسوم البيانية :

يمكن استخدام البرنامج لتمثيل بعض الرسوم البيانية على شكل أعمدة باستخدام الخلفية س ص  كما هو موضح بالشكل .

    (11)- الجبر  :

 بالطبع هناك أدوات للتعامل مع المقادير الجبرية افضل من قطع الأساس 10 ولكن يمكن استخدام هذه القطع لتمثيل بعض المقادير الجبرية وإجراء العمليات عليها ولكن القطع في هذه الحالة يصبح لها معانٍ مختلفة كما يلي :

القطعة الخضراء تمثل الوحدة وبالتالي فان خمس قطع خضراء تمثل الرقم 5 .أما القطعة الزرقاء فتمثل المجهول س ( لكنها لا تمثل عشر وحدات أبدا ) . وبالتالي 3 قطع زرقاء تمثل 3س . أما القطعة الحمراء فتمثل المجهول س² ( لكنها لا تمثل 100 وحدة أبدا ) . وبالتالي 7 قطع حمراء تمثل 7 س².وفي الشكل التالي نلاحظ أن :  (س+1)(2س² +3) = 2س² + 5س + 3 

  (12)- النسبة المئوية :

تعتبر مكعبات الأساس عشرة من انسب الوسائل لتمثيل النسبة المئوية لأنها قائمة على أساس الأعداد 10 ، 100 ، 1000  . إن الطبقة الواحدة ابتداء تمثل النسبة 100%  وعلى ذلك فان 3 قضبان تساوي 30%  وكذلك 9 وحدات تساوي 9% وهكذا .

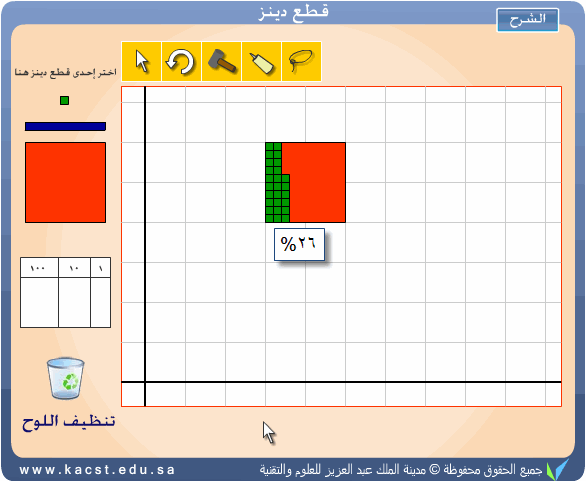
مسألة: إذا كانت نسبة الطلاب الراسبين في مادة العلوم في سنة ما يساوي 26% ، فكم عدد الراسبين إذا كان عدد الطلاب 350 طالبا ؟

الحل : يمكن تمثيل وحل هذه المسألة بكل بساطة باستخدام المكعبات كما يلي :

نمثل عد الطلاب الـ350 بمربع كامل (طبقة)  وعليه يكون كل مربع صغير يمثل 3.5 أي 350÷100 وعلى الشكل المقابل تمثل النسبة 26% بـ 26 وحدة

إذن كل وحدة تمثل 3.5 طالب

وعليه يكون عدد الطلاب = 26 × 3.5 = 91 طالباً