المقدمة 

يحتل التعليم مكانة كبيرة في حياة الشعوب ،لأنه أساس تقدم الدول و رقيها . ويرتكز التعليم في الدول المتقدمة على أهمية استخدام الوسائل التعليمية ،لأنها بمثابة الجسر الموصل بين المجرد و المحس.

 و لقد أوصى المجلس الوطني لمعلمي الرياضيات في الولايات المتحدة الأمريكية NTCM بضرورة إتاحة الفرصة أمام الطلاب لاستخدام الوسائل التعليمية التي تجسد المفاهيم الرياضية و تساعد على نقلها من المرحلة المجردة إلى المرحلة المحسة .

 و يرى برونرBRUNER  أن الأطفال قادرون على فهم العمليات بطريقة محسة أولا ، ثم بطريقة التعبير البياني المصور، و في النهاية يصبحون قادرين على فهم التمثيل بالرمز العددي و اللغوي المجردين ، و هذا التسلسل يتفق مع تصور بياجيه Piaget لنمو التفكير عند الأطفال إلا أن تكوين المفاهيم و استخدام أدوات تعليمية ووسائل مساعدة هو من فكر برونر. وهناك اجماع بين التربويين على أن تكوين المفاهيم هو حجر الزاوية بالنسبة للتعلم بصفة عامة و تعلم الرياضيات بصفة خاصة ،كما أجمع معظم علماء النفس على أن عملية التعلم تتطلب تعامل المتعلم مع الأدوات المساعدة مباشرة خاصة في المراحل الأولى منها.

ويعتبر الجبر من أكثر المواد صعوبة على العديد من الطلبة ،لما يحويه من مفاهيم مجردة ، إلا أن برونر كانت له محاولات عديدة في تقديم بعض المفاهيم المجردة بصورة حسية لطلاب المرحلة الابتدائية ، حيث قدم لهم مربعا كبيرا و عدد اخر من المربعات الأصغر مساحة من المربع الكبير، بالإضافة إلى بعض المستطيلات التي بعدها الأول مساو لطول المربع الكبير، و البعد الثاني مساو للمربعات الصغيرة ، و طلب منهم استخدام المربع الكبير و عدد من المربعات و المستطيلات الصغيرة لبناء مربع أكبر من المربع الأساسي في محاولة منه لتجسيد مفهوم (س+ص)2 =س2+2س ص+ص2 بصورة حسية ، و قد تمكن الطلاب فعلا من بناء مربعات أكبر من المربع الكبير على النحو التالي

إن تجسيد المفاهيم الجبرية في صورة حسية أو شبه حسية ليس جديدا، فقد كان للعلماء المسلمين السبق في تمثيل العديد من المفاهيم الجبرية ، بل و حتى حل بعض المعادلات هندسيا كما فعل الخوارزمي حيث تمكن من حل معادلات من الدرجة الثانية في مجهول واحد هندسيا مستخدما أسلوب الإكمال إلى المربع ، فالمعادلة س 2 + 10س = 39 يمكن حلها عن طريق إنشاء مربع مساحته س2 و عشرة مستطيلات مساحة كل منها س توضع مناصفة جوار ضلعي القائمة على النحو التالي

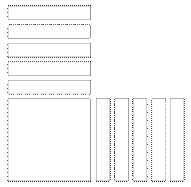
و لإكمال المربع نحتاج إلى إضافة 25 وحدة مربعة إلى طرفي المعادلة الأساسية على النحو التالي هندسيا

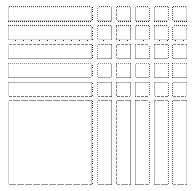
و جبريا على النحو التالي : س² + 10س + 25 = 39 + 25

و عليه فإن (س+5)2 =(8)2 أي أن طول ضلع المربع (س+5)يساوي 8 . أي أن س=3 . و لم يتطرق الخوارزمي إلى حل آخر للمعادلة.

و هناك العديد من المحاولات الجادة التي تهدف إلى تبسيط المفاهيم الرياضية إلى واقع محسوسو من تلك المحاولات مكعبات الأساس عشرة أو ما يطلق عليها مكعبات دينز، حيث أمكن اعتبار المربع الأساسي 10×10 بمثابة س×س و المستطيل الذي يمثل 1×10 بمثابة س ص

نظرا لأن له بعد مساو لبعد المربع الأساسي. أما المربع الصغير الذي يمثل الوحدة في الأصل يمكن اعتباره ص2 مما يمكننا من تمثيل العدي من المقادير الجبرية و ضربها.

فعلى سبيل المثال عملية ضرب (س+2ص) (س+ص) يمكن تمثيلها بقطع دينز على النحو التالي

يكون الناتج كما هو واضح من الرسم يساوي المربع الأساسي س2 و ثلاثة من المستطيلات 3س ص بالإضافة إلى وحدتين مربعتين مساحة كل واحد منها ص2 . و بالرغم من قوة هذه القطع إلا أنها عاجزة عن التفريق بين الثوابت و المتغيرات ، فهي و إن اعتبرت المربعات الصغيرة تنثل الثوابت و المستطيلات و المربعات الكبيرة تمثل المتغيرات ، تظل المتغيرات تمثل عددا محددا من الثوابت فالمستطيل الذي يمثل س ص مثلا عبارة عن عشرة من مربعات الوحدة الذي يمثل الواحد منها في هذه الحالة ص2 ، كما أن س2= 10 س ص.

و هناك العديد من المحاولات لتجسيد المفاهيم الجبرية منها استخدام الألوان للتفريق بين المقادير السالبة و المقادير الموجبة، فحاصل ضرب (س+ص) (س-2ص) يمكن تمثيله على النحو التالي

وذلك بإعطاء الجزء السالب لونا مغايرا للجزء الموجب و يكون الناتج كما هو واضح من الشكل السابق عبارة عن : س² – 2س ص – 2 ص² + س ص = س² – س ص 2ص² .

و بالرغم من تمكن هذا الأسلوب من معالجة القصور الموجود في مكعبات الأساس عشرة حيث اختار أبعادا مختلفة للقطع ، بحيث إن القطع التي اعتبرها متغيرات لم تعد تساوي عددا معينا من القطع التي تمثل الثوابت (الوحدة) إلا أن استخدامه الألوان في المقادير السالبة لا يمكن تعميمه بصورة عامة في الجبر فسالب س ليس بالضرورة أن يكون مقدارا سالبا ، هذا بالإضافة إلى أن المستطيل الذي يمثل المقدار (س+3ص)(س-4ص) هو ذات المستطيل الذي يمثل عملية ضرب المقدار (س-3ص)(س+4ص) .

مع اختلاف في الألوان و هذا مغاير للحقيقة حيث إن : (س+3ص) لا تساوي (س-3ص). كما أن (س-4ص) لا تساوي (س+4ص)

و الشكل التالي يوضح الفكرة :

و في الحقيقة هذه ليست كل المحاولات ، فهناك محاولات أخرى ألا أن بعضها تكرار لمحاولات سابقة و البعض الآخر فيه شيء من الصعوبة  على الطالب ، لذلك آثرنا التعامل مع معمل الجبرالحديث . و بالتحديد مع كتاب بعنوان Ageblocks من تأليف Anit Johnson قامت بنشره شركة  South Westen واعتبرناه مرجعا أساسيا بالإضافة إلى العديد من المصادر الأخرى التي تهتم بمعمل الجبر. و قد حصلت على موافقة من الناشر. و بالرغم من قدرة المعمل على حل الصعوبات التي واجهت غيره من المحاولات و تمكنه من تمثيل معظم المفاهيم الجبرية إلا أنه ليس باستطاعته التعامل مع مقادير أعلى من المقادير التكعيبية ، كما أنه يتعامل مع متغيرين فقط. و يظل عاجزا عن تمثيل بعض المقادير.

 و ما نود أن نؤكده هو أن التعامل مع معمل الجبر ليس الهدف منه الإجابة بحد ذاتها ، و إنما فهم لماذا الإجابة أصبحت بهذه الصورة ، إضافة إلى أن معمل الجبر يعالج موضوعات أخرى غير الجبر مثل المساحة و المحيط و الحجوم.