فيثاغورث ( 8 )

اضغط هنا لمشاهدة البرمجية

   اسم البرنامج :   فيثاغورث 8

 الهدف العام : تعميق مفهوم نظرية فيثاغورث لدى الطالب وربطها بمساحات المضلعات المنشأة على اضلاع المثلث القائم الزاوية

 بعض استخدامات البرنامج : 

• تطبيق  نظرية فيثاغورث على مختلف المضلعات المنتظمة .

• تحديد العلاقة بين الوتر وضلعي القائمة في المثلث القائم الزاوية ومساحة المضلع الثماني المنتظم المنشأ على كل منهما .

• تعميم العلاقة بين الوتر وضلعي القائمة على مساحة جميع المضلعات المنتظمة .

• تحديد أن الوتر أطول ضلع في المثلث القائم الزاوية .

شرح البرمجية وطريقة العمل :

تعتمد الفكرة الأساسية للبرنامج على تطبيق نظرية فيثاغورث من عدة أوجه وبإشكال مختلفة وباستخدام انواع مختلفة من المضلعات المنتظمة حيث تعرض البرمجية :

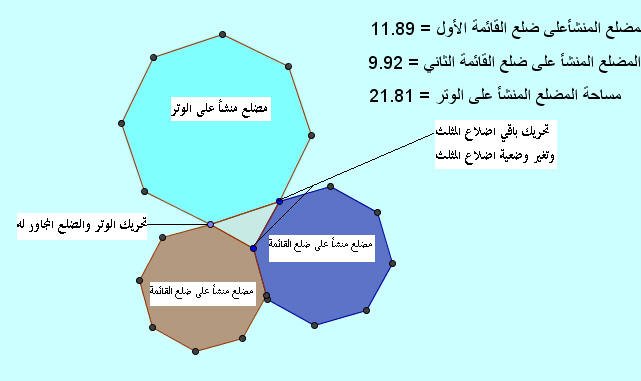
• مثلث قائم الزاوية منشأ على كل ضلع من ضلعي القائمة فيه مضلع ثماني منتظم طول ضلعه مساويا لطول الضلع  المنشأ عليه

•  ومضلع ثماني آخر منتظم منشأ على الوتر طول ضلعه مساويا لطول ضلع الوتر

•  بالاضافة إلى ثلاث نقاط لتحريك المثلث تكبيرا وتصغيراً أو تحريكه من مكان لاخر وتغيير وضعية مختلف أضلاعه .

 كما يتضح من الشكل التالي :

اللوحة ( 1 )

المادة العـــلمية :

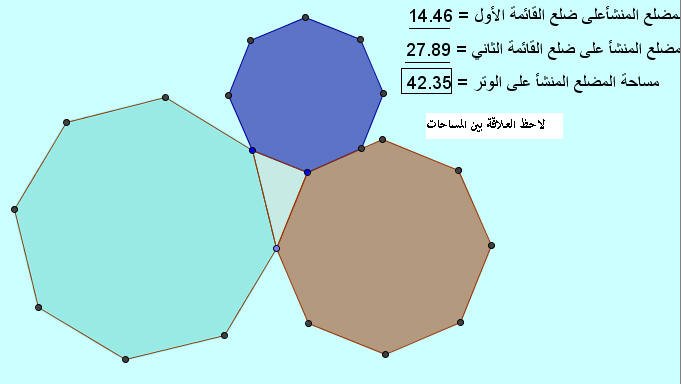
حرك النقاط الزرقاء لتحصل على شكل جديد ثم انظر إلى مساحات المضلعات الثمانية المنتظمة المنشأة على الأضلاع الثلاثة ماذا تلاحظ :

تلاحظ أن:

 مساحة المضلع المنتظم المنشأ على الوتر = مجموع مساحتي المضلعين المنشئين على ضلعي القائمة

 كما يتضح من الشكل التالي :

اللوحة ( 2 )

وبتحريك النقاط مرة أخرى نحصل على الشكل التالي :

اللوحة ( 3 )

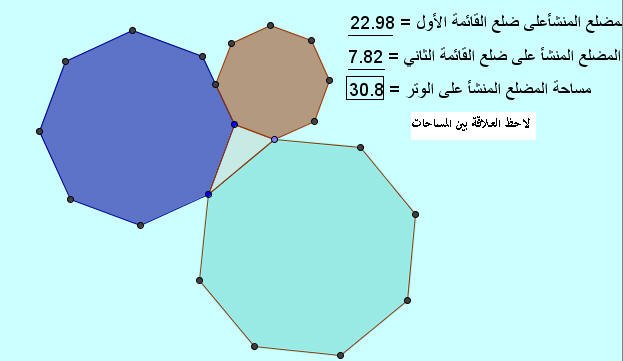
ولكن السؤال الآن : هل تختلف النظرية بتغير نوع المضلع  ؟؟؟

في الواقع ومن خلال مختلف المضلعات المنتظمة أمكننا استنتاج أن نظرية فيثاغورث مرتبطة بمختلف مساحات المضلعات المنتظمة والمنشاة على أضلاعه ولا تختص بمضلع معين وهذا يغير الفكرة السائدة المنتشرة إلى ارتباطها فقط بمساحة المربع وبالتالي يمكن إعادة صياغة نص النظرية كالتالي :

مساحة المضلع المنتظم المنشأ على الوتر = مجموع مساحتي المضلعين المنتظمين المنشئين على ضلعي القائمة

وما لاحظناه حصولنا على نفس المساحات ونفس الأطوال لمربع الوتر وضلعي القائمة مع إختلاف المضلعات وهذا يعني أن ألا نربط  بمربع الوتر بمساحة المربع  المنشأ على الوتر فقط ، بل أن مربع الوتر يعني مساحة أي مضلع طول ضلعه مساويا لطول ضلع الوتر منشأ على الوتر سواء كان ثلاثي أو رباعي  أو خماسي أو سداسي أو نوع آخر