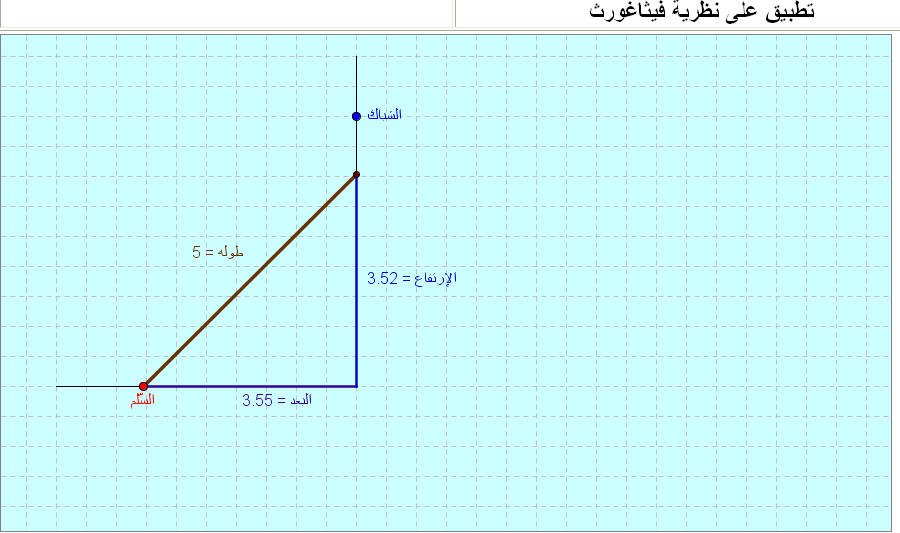
طول السلم
اسم البرمجية:طول السلم
اضغط هنا لمشاهدة البرمجية
الهدف العام :
1- اجراء تطبيقات مختلفة على نظرية فيثاغورس .
استخدامات البرمجية :
1- استنتاج طول السلم المثبت على جدار بدلالة ارتفاع الجدار وبعد قاعدة السلم عن قاعدة الجدار .
2- استنتاج ارتفاع الجدار بدلالة طول السلم المثبت عليه وبعد قاعدة السلم عن قاعدة الجدار .
3- استنتاج بعد قاعدة السلم السلم المثبت على جدارعن قاعدة الجدار بدلالة ارتفاع الجدار وطول السلم.
المادة العلمية :
1- نظرية فيثاغورس:
في مثلث قائم الزاوية مربع طول الوتر يساوي مجموع مربيعي طولي الضلعين الآخرين.
شرح البرمجية :
البرمجية على الشكل التالي :

أمثلة :
مثال1: احسب طول السلم المثبت على جدار إذاكان بُعد قاعدة السلم عن قاعدة الجدار(2.18م)وارتفاع الجدار حتى نقطة التلاقي(4.5م)
الحل: تقوم البرمجية بحساب طول السلم تلقائياً حسب نظرية فيثاغورس ( (طول السلم)2 = ( البعد)2 + (الارتفاع)2كما يتضح في الشكل التالي:
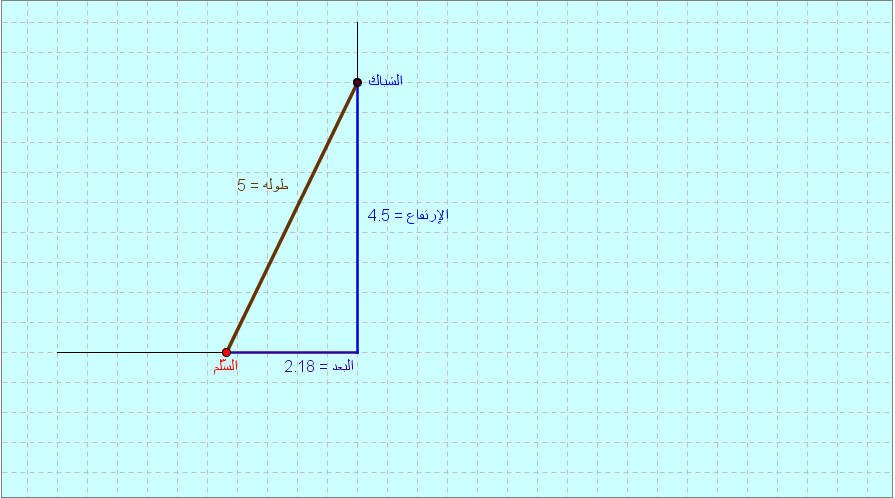
لاحظ أن طول السلم = 5م
مثال2: احسب طول السلم المثبت على جدار إذاكان بُعد قاعدة السلم عن قاعدة الجدار(5م)وارتفاع الجدار حتى نقطة التلاقي(0م)
الحل: تقوم البرمجية بحساب طول السلم تلقائياً حسب نظرية فيثاغورس ( (طول السلم)2 = ( البعد)2 + (الارتفاع)2كما يتضح في الشكل التالي:
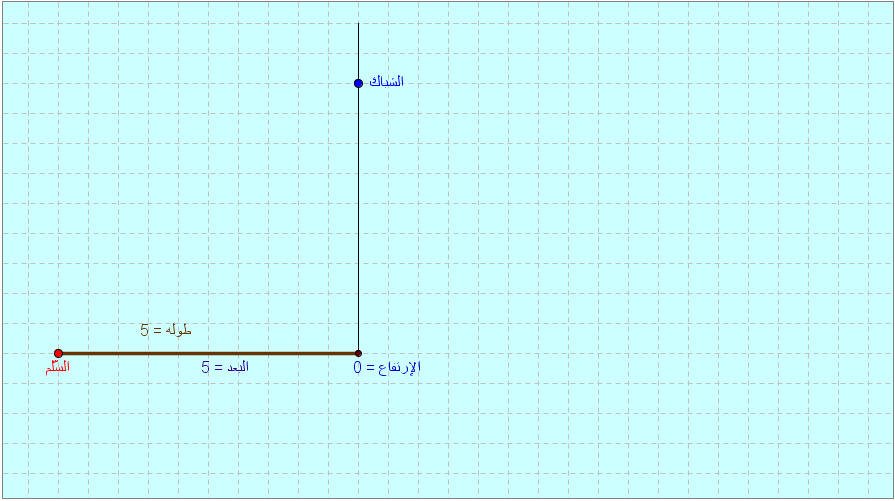
لاحظ أن طول السلم = 5م ،والاختلاف عن الحالة السابقة إنه في هذه الحالة لم يتم اسناد السلم على الجدار لكنه بقي على الأرض، فكان البعد = طول السلم
مثال3: احسب طول السلم المثبت على جدار إذاكان بُعد قاعدة السلم عن قاعدة الجدار(0م)وارتفاع الجدار حتى نقطة التلاقي(5م)
الحل: تقوم البرمجية بحساب طول السلم تلقائياً حسب نظرية فيثاغورس ( (طول السلم)2 = ( البعد)2 + (الارتفاع)2كما يتضح في الشكل التالي:
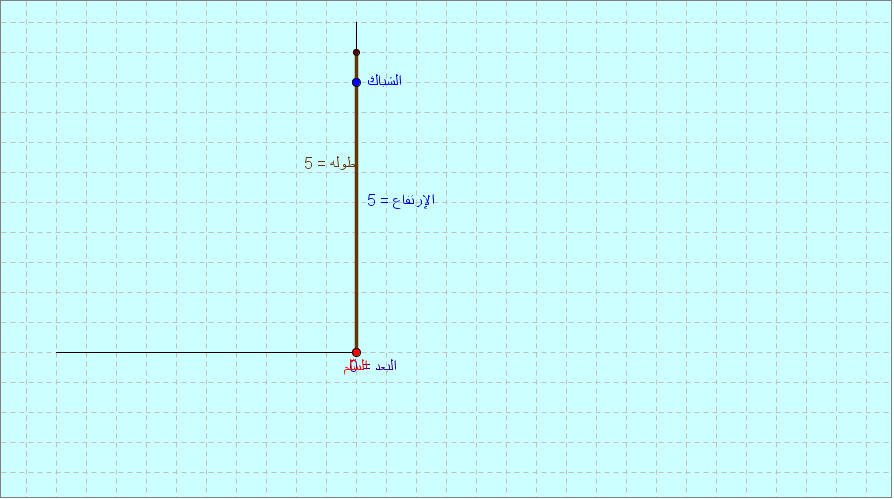
لاحظ أن طول السلم = 5م ،والاختلاف عن الحالتين السابقتين إنه في هذه الحالة تم إلصاق السلم بالجدار فكانت الزاوية بينهما= 0ْ، فأصبح الارتفاع = طول السلم .