الزوايا بين مستقيمين متوازيين

اضغط هنا لمشاهدة البرمجية

اسم البرنامج :   الرباعي الدائري

   الهدف العام : التعرف على الزوايا بين مستقيمين متوازيين والعلاقة بينها

 بعض استخدامات البرنامج : 

•  تحديد أنواع الزوايا المختلفة بين مستقيمين متوازيين وقاطعهما .

•  تحديد مجموع الزوايا بين مستقيمين متوازيين .            

• تمييز العلاقة بين الزوايا بين مستقيمين متوازيين وقاطعهما .

• إيضاح العلاقة بين الزوايا المتساوية بالتبادل والتناظر والمستقيمين المتوازيين .

شرح البرمجية وطريقة العمل : 

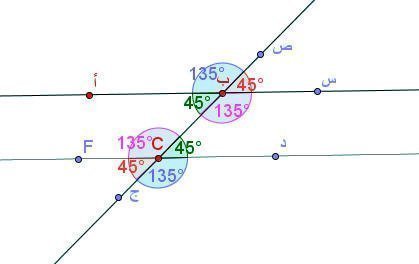
اللوحة ( 1 ) 

•  النقطة أ وتستخدم  لتغيير وضع المستقيمين المتوازيين 

• النقطة ب وتستخدم لتغير قياس الزاوية ب

• النقطة س لتحريك المستقيم الواقعة علية لأعلى أو لأسفل ولتحريك المستقيم القاطع .

• النقطة ص لتحريك المستقيم الواقعة علية ( القاطع ) نحو اليمين أو اليسار

• النقطة C تستخدم لقياس الزاوية C .

• النقطتان د ، F لتحريك المستقيم الواقعة عليه لأعلى أو لأسفل ولتحريك المستقيم القاطع .

المادة العــلمية

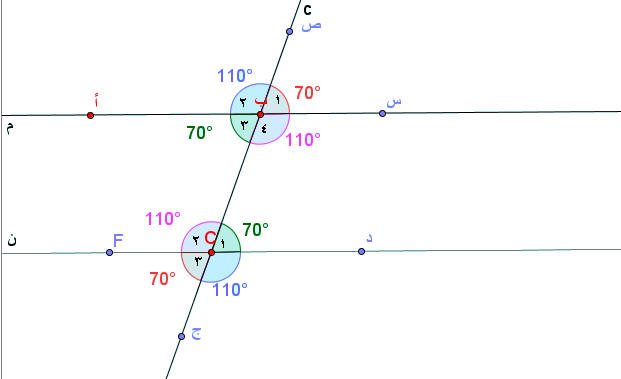
اللوحة ( 2 )

مجموع الزوايا بين مستقيمين متوازيين يساوي 180 ْ

اللوحة ( 2 )

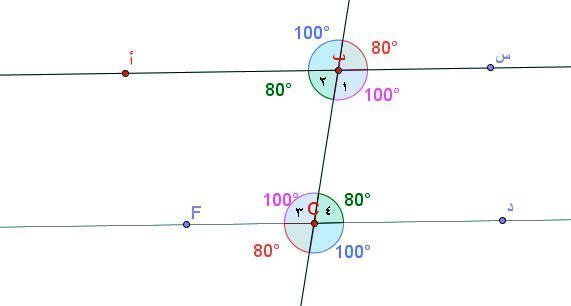
من خلال اللوحة السابقة نجد أن :

زاوية 1 =زاوية 3 = 100 ْ  ( بالتبادل )

زاوية 2 = زاوية 4 = 80 ْ ( بالتبادل )

نلاحظ أن كل زاويتين متساويتان محصورتان بين المتوازيين وفي جهتين من القاطع نسميهما متبادلتين

إذا قطع مستقيم مستقيمين متوازيين فكل زاويتين متبادلتين متساويتين .

والعكس صحيح

إذا تساوت زاويتين متبادلتين بالنسبة لمستقيمين  وقاطعهما ، كان المستقيمان متوازيان .

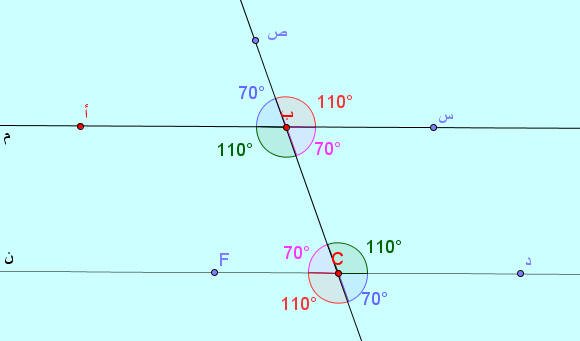
اللوحة ( 3 )

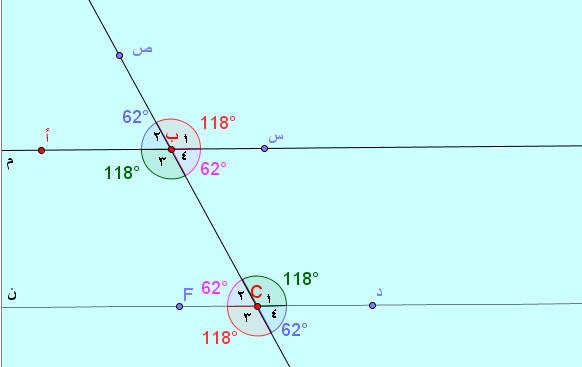
كل زوج من الزوايا التالية يسمى زوايا متناظرة

( ب1 ، C1 ) ، ( ب2 ، C2 ) ، ( ب3 ، C3 ) ، ( ب4 ، C4 )

وعموما كل زاويتين  إحداهما داخلية والأخرى خارجية بالنسبة للمتوازيين وفي جهة واحدة من القاطع

نسميهما زاويتين متناظرتين

إذا قطع مستقيم مستقيمين متوازيين فكل زاويتين متناظرتين متساويتين .

والعكس صحيح

إذا تساوت زاويتين متناظرتين بالنسبة لمستقيمين وقاطعهما ، كان المستقيمان متوازيان .

اللوحة ( 4 )

بتحريك أي من النقاط نلاحظ تغير في قياسات الزوايا وبملاحظة الزوايا المتبادلة والمتناظرة نجد أن :

الزوايا المتبادلة متساوية وكذلك الزوايا المتناظرة .

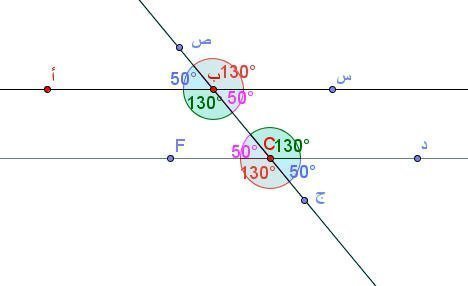
كذلك بتحريك النقاط مرة أخرى نجد تساوي للزوايا المتناظرة والمتبادلة

اللوحة ( 6 )