الرباعـي الدائــري

اضغط هنا لمشاهدة البرمجية

اسم البرنامج :   الرباعي الدائري

   الهدف العام : التعرف على الرباعي الدائري وعلاقته بالدائرة  .

 بعض استخدامات البرنامج : 

•  تعريف الرباعي الدائري .

•  تحديد مجموع زوايا الرباعي الدائري  .             

• إيضاح خاصية الزوايا المتقابلة في الرباعي الدائري

• إيجاد العلاقة بين كل رباعي به زاويتان متقابلتان متكاملتان والرباعي الدائري .

• استنتاج علاقة هل كل شكل رباعي دائريا .

شرح البرمجية وخطوات العمل : 

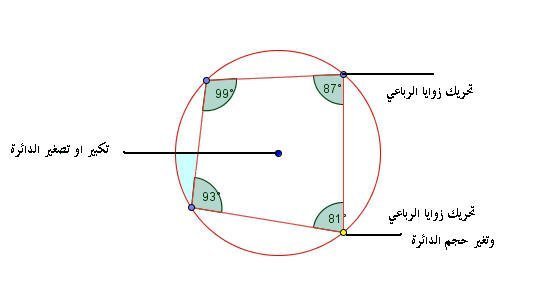
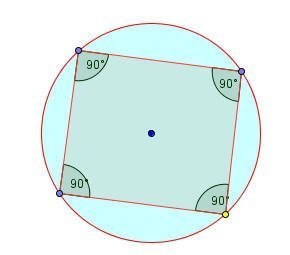
اللوحة ( 1 )

الشكل التالي يوضح أجزاء البرمجية :

بتحريك أي من النقاط الموضحة بالشكل يتغير وضع الرباعي الدائري ويكون في كل حالة رؤوسه واقعة على محيط الدائرة ومجموع زواياه 360 ْ وكل زاويتان متقابلتان فيه مجموعهما 180 ْ

المادة العــلمية :

اللوحة ( 1 ) :

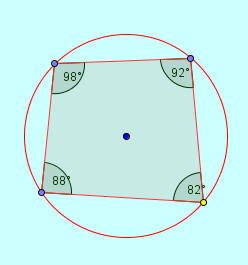
الرباعي الدائري هو : كل شكل رباعي رؤوسه تقع على الدائرة

وبملاحظة الشكل السابق نجد أن مجموع زواياه الأربع = 82 ْ + 98 ْ+92 ْ+88 ْ = 360 ْ

ونلاحظ انه مهما تغير وضع الرباعي  يبقى مجموع الزوايا الأربع ثابتا .

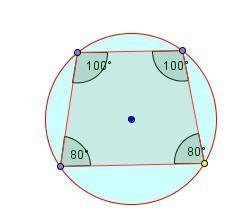
اللوحة ( 2 ) : 

في أي رباعي دائري كل زاويتين متقابلتين متكاملتان مجموعهما 180 ْ

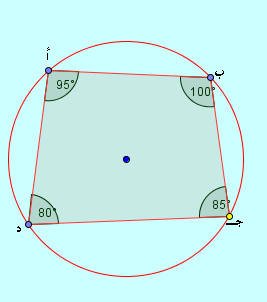
وبتحريك النقاط الأربع بملاحظة زوايا الرباعي نجد أن :

< أ + < جـ = 180 ْ

< ب + < د = 180 ْ

وبذلك تكون كل زاويتين متقابلتين متكاملتين

اللوحة ( 3 ) : 

بتحريك النقاط للحصول على زوايا متعددة للشكل وبجمع كل زاويتين متقابلتين  يكون مجموعهما 180 ْ وعند النظر إلى الشكل في كل مرة نجده رباعي دائري 

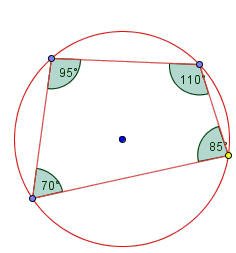
 إذا وجد في رباعي زاويتان متقابلتان متكاملتان فانه يكون رباعيا دائريا

اللوحة ( 4 ) :   

إذا سألنا أنفسنا أي من الأشكال التالية :

                              المستطيل - المربع - المعين - متوازي الأضلاع - شبة المنحرف

المستطيل والمربع يمثلان رباعي دائري كما يتضح من الشكل بتحقق الشرط وهو أن كل زاويتين متقابلتين متكاملتين

شبة المنحرف أيضا يمثل رباعي دائري من خلال تحقق الشرط .

أما متوازي الأضلاع والمعين فهما لا يمثلان رباعي دائري أبدا .

   أمثلة :

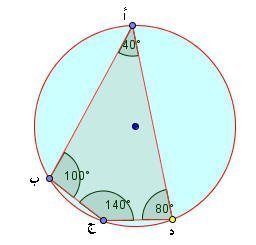
 أ ب ج د رباعي دائري  زاوية أ = 40 ْ   ، زاوية ب = 100 ْ اوجد قياس زاويتي  ج ، د

حل المثال :

من خلال تحريك النقاط نحاول الحصول علي قياس لزاوية  أ = 40 ْ وكذلك زاوية ب = 100 ْ ثم نرجع للشكل فنحصل على قياس زاويتي ج ، د كما يتضح من الشكل .

اللوحة ( 5 ) :  

اللوحة ( 6 ) :  

إذا كانت   زاوية أ = 89 ْ   ، زاوية ب = 81 ْ هل الرباعي دائري ثم  اوجد قياس زاويتي  ج ، د

الحل : نرجع للبرمجية ثم نحاول تحريك الزوايا للوصول للزاويتين المعطاة ، فيكون الشكل بالصورة التالية :

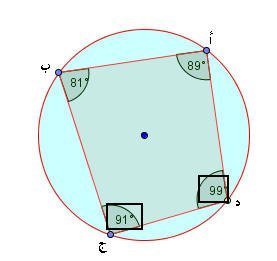
واضح أن الشكل رباعي دائري من خلال أن الزاويتين المتقابلتين مجموعهما 180 ْ