التناظر حول نقطة

اضغط هنا لمشاهدة البرمجية

اسم البرنامج :   التناظر حول نقطة

  الهدف العام :  التعرف على التناظر حول نقطة وتمييز خواصه  .

 بعض استخدامات البرنامج : 

• تحديد خصائص التناظر حول نقطة وتطبيقها

• الاستدلال على تطابق مساحات الأشكال المتناظرة حول نقطة

• الاستدلال على أن التناظر حول نقطة يحافظ على الأطوال والزوايا

• الاستدلال على أن التناظر حول نقطة يحافظ على التعامد .

• استنتاج  مركز تناظر الأشكال المتناظرة .

شرح البرمجية مع خطوات العمل :

تعتمد فكرة البرمجية على توضيح مفهوم  التناظر حول نقطة لدى الطالب وتميزه عن التناظر حول محور من خلال عرض لوحة تتضمن مثلث (  أ ب جـ ) في مستوي الاحداثي تحدده ثلاث نقاط  ( أ ، ب ، جـ ) لتحريكه  والتغير من وضعيته ونوعه ، وعند تحريك هذا المثلث ينتج تحريك لمثلثين أحداهما في الربع الثاني من المستوي الاحداثي والآخر في الربع الثالث بحيث يكونان صورة طبق الأصل للمثلث الذي تم تحريكه كما يتضح من :

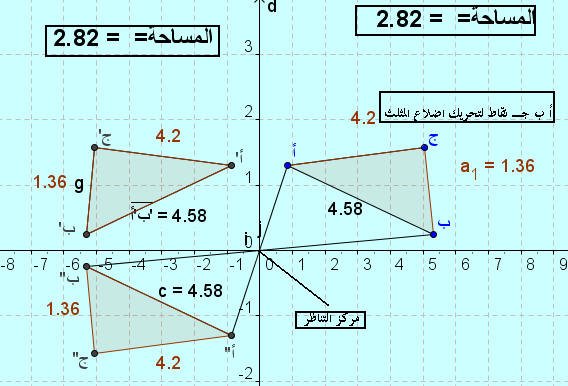
  اللوحة رقم ( 1 )

نلاحظ أن النقطة ( j ) تقع في منتصف المسافة بين [ أ أ ً ] وبالتالي فهي تعتبر نقطة التناظر ( مركز التناظر )

وبمقارنة الأشكال الثلاثة نجد أن لها نفس قياس أطوال الأضلاع ونفس قياس الزوايا  حيث نلاحظ أن طول :

 | أ ب  | =  | أ َ بَ |=  4.58سم =  | أ ً بً  |

 |أ جـ  | =  | أ َ جـ َ  | = 4.2سم =  | أ ً جـ ً | 

( فالتناظر حول نقطة يحافظ على الأطوال )

و نلاحظ تطابق المثلثين ( أ ب جـ ) و ( أ ً ب ً جـ ً ) من خلال التناظر حول نقطة

أي أن التناظر حول نقطة يحول كل شكل إلى شكل مناظر له

المادة العلمية

التناظر حول نقطة هو تقابل يحول كل نقطة ب الى صورتها بَ بحيث تقع النقطة م في منتصف المسافة بينهما

تسمى النقطة م مركز التناظر

          اللوحة رقم ( 2 ) :

بتحريك النقاط الخاصة بالمثلث ( أ ب جـ ) ينتج لنا الشكل التالي :

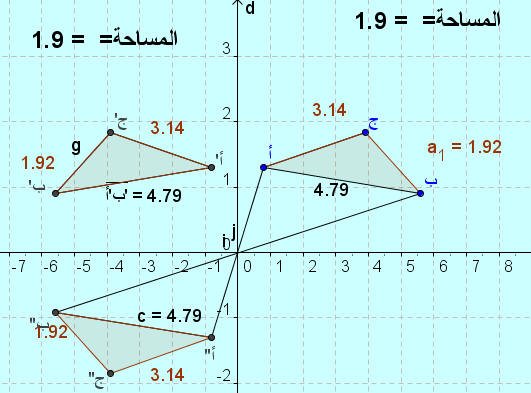
ونلاحظ من اللوحة أن المثلثين ( أ ب جـ ) ، ( أ ً بً جـ ً ) متناظران حول نقطة ( J )  ( مركز التناظر ) ، وهذا واضح من تطابق الشكلين كما أوضحنا في اللوحة السابقة .

     اللوحة رقم ( 3 ) :

 بتحريك إحدى النقاط في المثلث ( أ ب جـ ) :

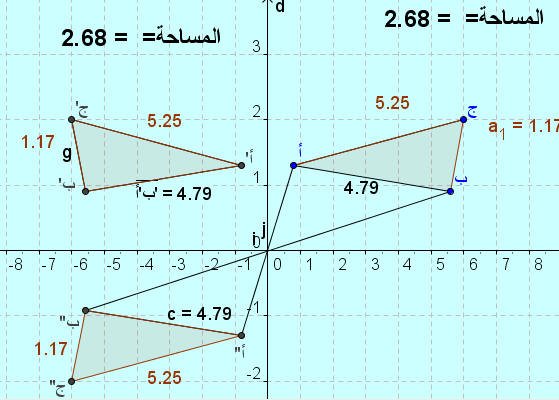
أيضا نحصل على شكلين متناظرين حول نقطة لهما نفس الأطوال ونفس المساحة

كما نلاحظ انه في كل مرة نحرك فيها نقاط التحريك ينتج لنا مثلثين متناظرين حول نقطة ومثلث آخر ( أ َ بَ جـَ ) هو صورة طبق الأصل للمثلثين ناتج  من خلال التناظر حول محور للمثلث وصورته

     اللوحة رقم ( 4 ) :

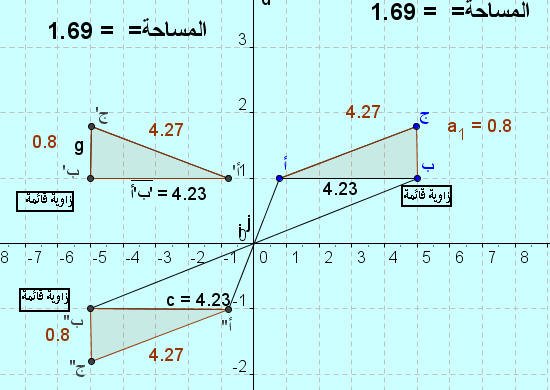
نلاحظ من خلال اللوحة السابقة الحصول على صورة للمثلث بالتناظر حول نقطة وكذلك بالتناظر حول محور

كما نلاحظ أن التناظر حول نقطة حافظ على الزوايا حيث حول الزاوية القائمة في المثلث ( أ ب جـ ) إلى زاوية قائمة في المثلثين الآخرين كما ننستدل على أن التناظر حول نقطة حافظ على التعامد

 اللوحة رقم ( 5 ) :

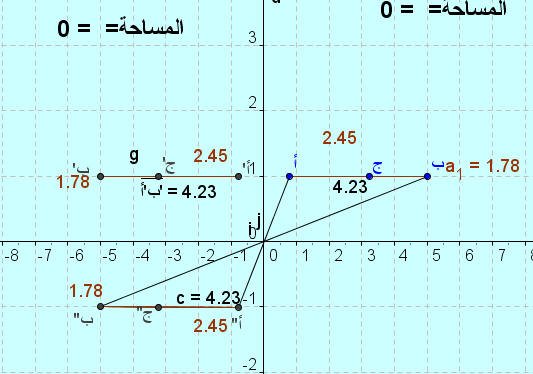
نلاحظ من خلال الشكل أن التناظر حول نقطة حول القطعة المستقيمة [ أ ب ] إلى قطعة مستقيمة أخرى مناظرة لها هي [ أ ً بً ]

أي أن التناظر حول نقطة هو تقايس