التناظر حول محور

اضغط هنا لمشاهدة البرمجية

   اسم البرنامج :   التناظر حول محور

  الهدف العام :  التعرف التناظر حول محور وتحديد خواصه

 بعض استخدامات البرنامج : 

• تعريف التناظر حول محور

• تحديد صورة نقطة بالتناظر حول محور

• إثبات أن التناظر حول محور يحافظ على الأطوال

• تعريف بالمستوى الاحداثي والأرباع الأربعة

• تحديد متى تكون النقطتان متناظرتان .

شرح البرمجية مع خطوات العمل :

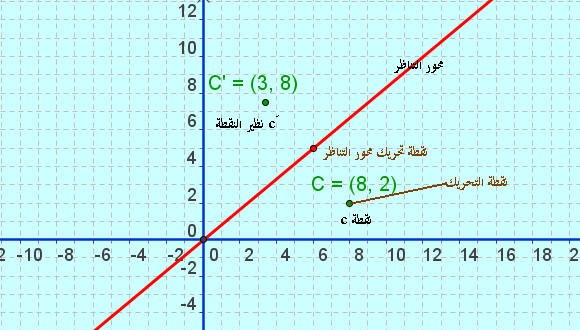
تعتمد فكرة البرمجية على تعميق مفهوم التناظر حول محور لدى الطالب من خلال تحريك النقطة ( c ) في المستوي الاحداثي باستخدام النقطة الخضراء حول المستقيم الأحمر ( محور التناظر ) وبتحريك النقطة في المستوي ، نجد أن هناك نقطة أخرى تتحرك تبعا لتحرك النقطة ( c ) هي  النقطة ( cَ )  صورة النقطة ( c )

 ونستطيع أن نوضح ذلك كما يلي :

  اللوحة رقم ( 1 )

من خلال الشكل نلاحظ أن المستقيم الأحمر   يقع في منتصف المسافة بين النقطتين ( c ، c َ )

لذلك نسمي هذا المستقيم محور التناظر ونسمي هذه العملية التناظر حول محور

وبتحريك النقطة ( c ) مرة أخرى نلاحظ ما يلي :

      اللوحة رقم ( 2 )

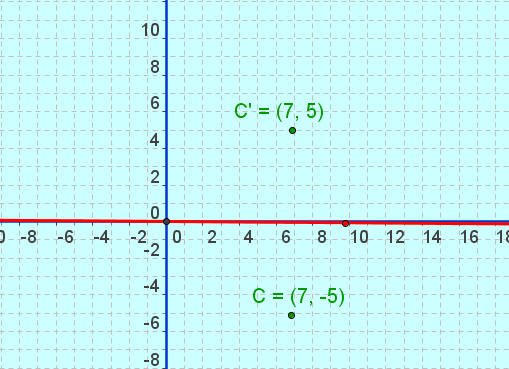
ونلاحظ أن بعد كل من النقطتين متساوي عن محور التناظر( المستقيم الأحمر ) وهذا البعد  يساوي ( 5 ) وحدات .

وبذلك تكون النقطتان  ( c ، c َ ) متناظرتان حول محور التناظر .

وبذلك يكون :

المادة العـــلمية

التناظر حول محور هو " هو تقابل يحول كل نقطة c من المستوي إلى نقطة c  َ بحيث المستقيم هو العمود المنصف للقطعة المستقيمة

[ c ، c َ ]

يسمى هذا المستقيم محور التناظر ويقع في منتصف المسافة بين النقطتين

   اللوحة رقم ( 3 )

وبتكرار العملية من خلال تحريك النقطة الخضراء لتغير وضع النقطة ( c ) أو النقطة الحمراء لتغيير وضع المستقيم نجد أن في كل مرة نحصل على نقطة جديدة ( cَ )  هي صورة للنقطة ( c ) .

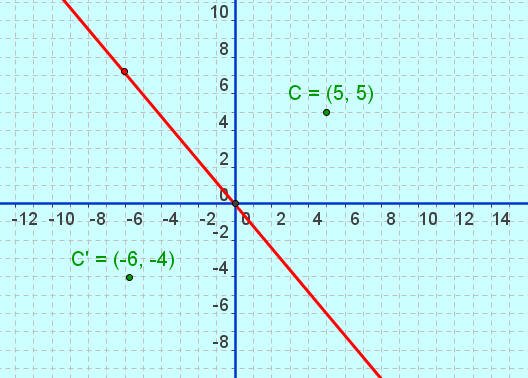
ويتضح من خلال هذه اللوحة أن التناظر حول محور يحول كل نقطة إلى نقطة وبالتالي نستطيع تعميم ذلك بقولنا أن التناظر حول محور يحول كل شكل إلى شكل مناظر له

  اللوحة رقم ( 4 )

مثال ( 1 ) : أوجد نظير النقطة ( -3 ، 9 ) بالتناظر حول المستقيم

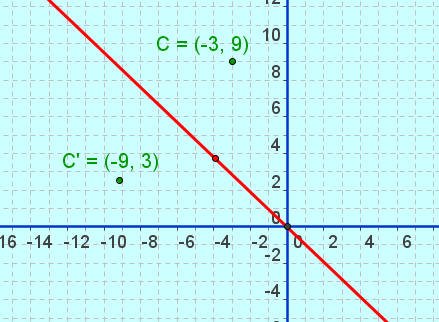
بتحريك النقطة إلى مكانها المناسب في الربع الثاني من المستوى الإحداثي نجد أن هناك صورة لهذه النقطة هي ( -9 ، 3 )

وهكذا يمكن تكرار ذلك بأخذ عددا من النقاط وإيجاد صورها بالتناظر حول محور