المتسـلسـلات
إن مفهوم المتتابعة يلعب دورا كبيرا في البناء الرياضي والتطبيقات ومجموع حدود المتتابعة يسمى متسلسلة
إذا أردنا اكتشاف مجموع أي عدد من حدود المتتالية المتتالية من متسلسلة الأعداد الطبيعية : ( 1 ، 2 ، 3 ، 4 ، ...,....,.... ابتدأ من الواحد ، يشكل عدد مثلثى على النحو التالي : نقوم ببناء الأعداد المتتالية بالمكعبات المتداخلة
فنلاحظ أن العدد المثلث الثالث فهو مثلث فيه ثلاث مكعبات على كل جانب ، وهذا العدد ناتج ( 1 + 2 + 3 = 6 ) وينتج ذلك كما يلي:
1 = 1
+2 = 3
+ 3 = 6
+ 4 = 10
+ 5 = 15
+ 6 = 21
وهكذا نستطيع الانتقال من عدد الى العدد الذي يليه وبملاحظة العمليات التالية :
1 + 2 = 3
بجمهما مرتين ينتج مستطيل 2 في 3 كما يلي

أي 2 × 3 ÷ 2 = 3
وبالطريقة نفسها يكون 1 + 2 +3 = 6
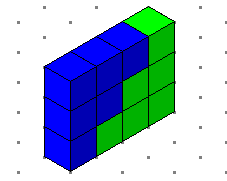
أي 3× 4 ÷ 2 = 6
بجمهما مرتين ينتج مستطيل 3 في 4 كما يلي
وبالطريقة نفسها مجموع 1 + 2+ 3 + 4 +5=15
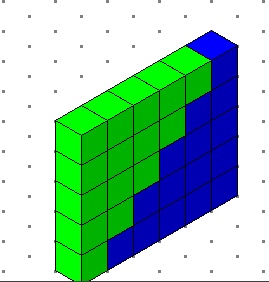
بجمهما مرتين ينتج مستطيل 5 في 6 كما يلي
أي 5 × 6 ÷ 2 = 15
ولايجاد عدد المكعبات نقوم بناء شكل مماثل لكل شكل ويلاحظ أن عدد مكعبات العدد الثاني تساوي نصف مكعبات المستطيل
- اذن ناتج الجمع = ( العدد ( العدد + 1 ) ÷ 2
لذا فان 1 +2 + .....+......+.......+ ن = نصف حاصل الضرب ن ( ن + 1 )
مج ن = ن (ن +1 ) / 2
تطبيــق :
المطلوب معرفة جمع : 1 + 2 + 3 + .....+ 56 = ؟ مباشرة
56 ضرب 57 قسمة 2
نشــاط : يمكن شرح السابق بالمربعات الملونة
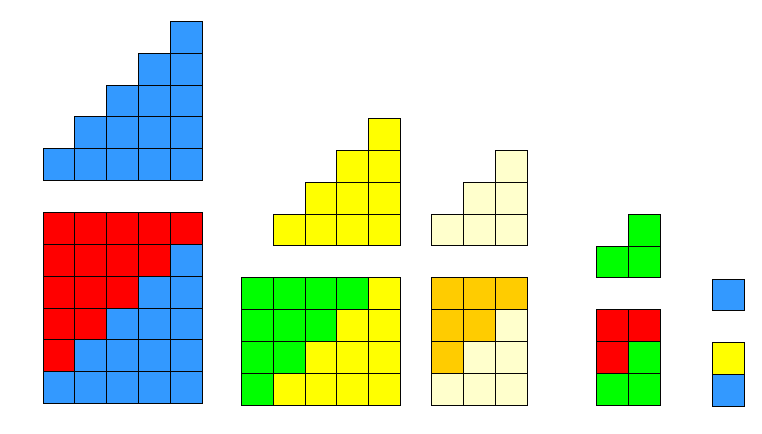
مجموع من واحد الى العشرة
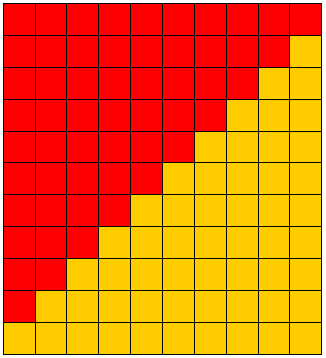
![]()
مجموع الاعــداد الفرديــة مج( 2ن - 1)
المتتالية : 1، 3 ، 5 ، 7 ، ...,....,......, تسمى الاعداد الفردية الممثلة بالشكل التالي:
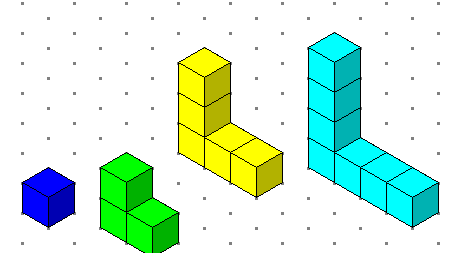
|
هناك قاعدة : اذا أضيف عدد فردى الى عدد مربع كان الحاصل عددا مربعا آخر |
ولتوضيح ذلك بشكل محسوس بالنسبة للاعداد الفردية عند جمعها نقول ما يلي:
(1 ) مربع إذا أضفنا إليه العدد (3 ) فيكون الناتج :
1 = 1
+ 3 = 4 = 2 × 2
4 + 5 = 9 = 3 × 3
9 + 7 = 16 = 4 × 4
16 + 9 = 25 = 5 × 5
ولتوضيح ذلك بالرسم تبين لنا :
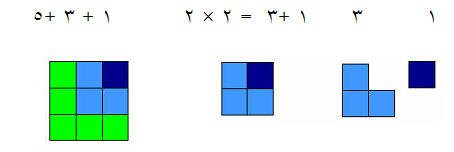
1 + 3 = 4 مربع طول ضلعه ( 2)
4 + 5 = 9 مربع طول ضلعه ( 3 )
وتوضيح العمليات : -
1 + 3 = 4 يعني 2 × 2 = 4
1+ 3 + 5 = 9 يعني 3 × 3 = 9
1 +3 + 5 + 7 = 16 يعني 4 × 4 = 16
اذن مجموع الحدين الأول والثاني مربع مساحته (4) أى 2 × 2 = (2 )2
ومجموع الثلاث حدود الفردية الأولى مربع مساحته (9) أى 3 × 3 = ( 3) 2
اذن مجموع عدد من الأعداد الفردية المتتالية عددها ن والمبدوئة بالواحد تساوي مربع مساحته ( ن × ن )
اذن 1 + 3 +5 + .....+......+......+ (2 ن -1 ) = (ن)2
الأعــداد الزوجيـــة مج ( 2 ن )
لايجاد مجموع حدود المتوالية المكونة الاعداد الزوجية سينتج القانون باستخدام المكعبات المتداخلة تكوين الاعداد:
- نقوم بنناء الاعداد الزوجية باستخدام المكعبات
2 ، 4 ، 6 ، ..... وهكذا يستطيع ان تحدد أى حد من حدود هذه المتوالية
لان 2 ، 4 ، 6 ، 8 ، ........، 2 ن كما هوموضح بالرسم

- عند جمع أي عددين زوجيين يكون الناتج عددا زوجيا كما سبق وأوضحنا
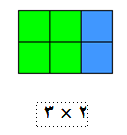
- أذن عند جمع الحدين الأول والثاني فى الاعداد الزوجية ، فلا بد أن يكون الناتج مستطيلا لانه يمثل عدد زوجي كذلك 0فنجد ان 2 + 4 = 6
يمثل مستطيل مكون من (6) مكعبات تمثل مساحة هذا المستطيل حيث بعداه ( 2 ، 3 )
- عند جمع الثلاث حدود أولالى كذلك : 2 + 4 + 6 + = 12 يمثــل مستطيل بعداه 3 ، 4 مساحته 12 أي 3 × 4

- وجمع الاربع حدود : 2 + 4 + 6 + 8 = 20 مستطيل بعداه :
( 4 ، 5 ) مساحته ( 20 ) مكون من ( 20 ) مكعب كما في الشكل التالي:
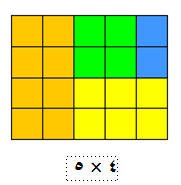
وبالطريقة نفسها نجمع الخمسة الأعداد الزوجية الأولى على النحو التالي:
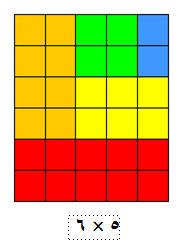
مجموع عدد (ن) من الحدود فى هذه المتسلسلة من الاعداد يساوى : ن(ن + 1 )
2 + 4 + 6 + 8 + ......... + 2ن = ن(ن+1 ) حيث أن
اذن مجموع 2ن = ن ( ن + 1 )
الشكل التالي يمثل مجموع العشرة حدوود الزوجية الأولى وهو مستطيل بعده الأول عدد الحدود التي نريد جمعها وبعده الثاني العدد الدي يليه
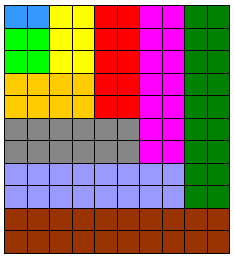
وهناك طريقة أخرى لتمثيل الأعداد الزوجية على النحو التالي :
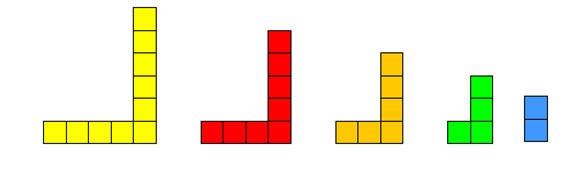
ويكون المجموع كما في الشكل التالي :
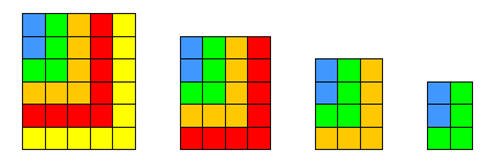
مجموع مربعــات الأعــداد الصحيحة ( مج ن2)
الأعداد : (1 )2 ، ( 2)2 ، ( 3)2 ، (4)2 ,..........
1 ، 4 ، 9 ، 16 ، .........
تمثل عبارة عن متوالية من مربعات الاعداد
فاذا أردنا معرفة مجموع حدود هذه المتوالية فاننا نستنتج قانون التسلسلة ن2
- ونقوم بتوضيح الاعداد ( 1) 2 بواسطة المكعب
- والعدد الآخر (2 )2 ممثل فى المساحة ( 2× 2) المكعب سطحه يمثل المربع والعدد الثالث ممثل فى المساحة ( 3 × 3 )
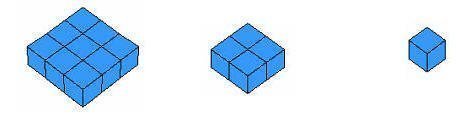
- لجمع الاعداد الثلاثة الأمربعة الأولى مع بعضها ينتج الشكل التالي :
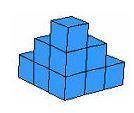
- في الخطوة الثالثة نقوم بعمل ثلاثة أشكال من الشكل الناتج على النحو التالي :
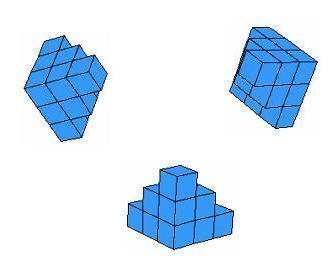
ويتم تجميعها لتكوينالشكل التالي
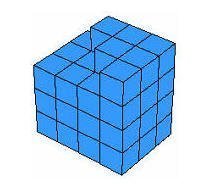
والجزء
العلوي 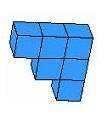
يمكن قصه الى نصفين متساويين حتى يكتمل الموشور وتكون أبعاده 3 وهو عدد الحدود ن و 4 وهو العدد الدي يلي عدد الحدود ( ن+1) و3ونصف
نصف حاصل ضربهما أي ن( ن+1)/2
والشكل التالي يوضح المقصود:
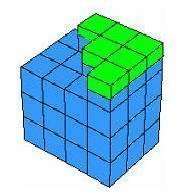
حيث يكتمل الموشور بإضافة النص الآخر الى الشكل العلوي ويصبح حجمه ( مجموع المكعبات ) يساوي حاصل ضرب أبعاده الثلاثة
ن في (ن + 1 )في (ن + 1/2)
وبتبسط حاصل الضرب نجد أن الحجم الكلي للموشور= ن(ن+1)(2ن+1) /2
ولكون الموشور مكون من ثلاثة قطع متطابقة يكون مجموع (1)2 + ( 2 )2 + ( 3 )2 يساوي ثلث حجم الموشور وبصورة عامة فإن:
(1)2 + ( 2 )2 + ( 3 )2+ 000000 + ن 2 = ن(ن+1)(2ن+1 ) / 6
مكعبــات الأعــداد ( ن3 )
مكعبات الأعداد : 1 ، 2 ، 3 ,......,.......
تمثل : 1 ، 8 ، 27 ، .......,......, متوالية عددين تمثل مكعبات الاعداد
الشكل التالي يمثل المكعبات الثلاثة الأولى :
|
|
|
|
|
1× 1× 1 = 1 |
2 × 2× 2 =8 |
3 × 3 × 3 =27 |
ولايجاد مجموع مكعبات الاعداد أي استنتاج قانون المتسلسلة
مج ن3 = (1)3 + (2 )3 + (3 )3 +.........+ ن3
باستخدام المكعبات المتداخلة :
- بيعاد ترتيب المكعب الدي طول حرفه ( 2 ) على النحو التالي
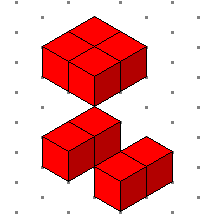
- يضاف (1)3 + (2 )3 = ( 1+ 8 ) = 9 بعد إعدة الترتيب ينتج لدينا الشكل التالي

وهو مربع طول ضلعه = 1+2
المكعب الذي طول ضلعه (3) مكعبات يعاد ترتيبه لثلاث طبقات على النحو التالي
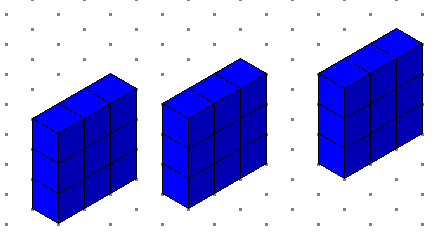
ويتم إضافته للشك السابق على النحو التالي:
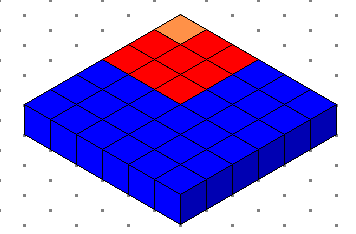
- بعد اضافة (3 )3 يصبح المقدار : (1) + (2 ) + (3 ) = 9 +27 = 36
- وتكرار العملية :
(1 ) + (2) + (3) + (4) = 36 +64= 100
نجد انه ينتج عبارة عن مكعب ابعاده (ن × ن × 1 )
فاذا نظرنا الى السطح للشكل يكون عبارة عن مربع مساحته ( ن)2 بعد ترتيبه
- يكون طول الضلع ممثل في حالة جمع الاربع حدود الاولى
1+ 2 + 3 +4 = 10
- اذن مساحة المربع تكون = (10)2 = 100
بما أن ن = 1 +2 + 3 +4 +.....+ ن = مربع المقدار ( ن(ن+1 ) /2 )
تصبح مساحة المربع ( ن)2 = ن(ن+1 )/2
مج(ن)3 = مج( 1+2 +3 +....+.... + ن )2
= (ن(ن+1)/2 )2
ايجـاد ( مج مج ن)
نشــاط :
الشكل التالي تم بناءه بعدد من المكعبات فيلاحظ ن :
الشكل عدد المكعبات
1 1
2 3
3 6
4 10
5 15
6 21
7 28
.. .. وهكذا
نجد إنها تمثل مجموعة الاعداد الطبيعية ( ن = ن(ن +1) /2
إذا أردنا معرفة الحد الرابع = 4 ×5 /2 = 10
وكذلك الحد العاشر يصبح = 10 × 11 /2 = 55
ولكن إذا أردنا معرفة مجموع هذه المتسلسلة أي استنتاج قاعدة لها أى ايجاد قانون مج مج ن وهو مجموع المجموع
مج مج ن = مج ن(ن+1) /2 = مج ( ن2+ن) /2 = نصف ( مج ن2 + نصف مج ن )
= نصف [ ن(ن+1)(2ن+1) /6 + ن (ن+1) /2 ] وبتبسيط الكسرين بتوحيد المقاميين نحصل على
= نصف [ ن(ن+1)(2ن+1) + 3ن (ن+1) ] /6
= نصف [ ن(ن+1) (2ن+1+3) ]/6
= نصف [ ن(ن(ن+1)(2ن+4)] /6
= نصف × 2 × ن(ن+1)(ن+2) /6
= ن(ن+1)(ن+2) /6

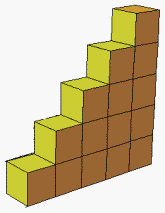

نشـــاط:
الشكل المرسوم مكون من عدة طبقات

- كم عدد من المكعباتاللازمة لبناء مثل هذا الشكل ؟
- كيف التوصل الى معرفة عدد المكعبات فى احد الأدوار ؟
- كيف يمكن ايجاد قاعدة تحدد عدد المكعبات فى هذا الجسم
نلاحظ ان الدور الواحد يمثل مستطيل مساحته ( 1 × 2 )
والدور الذي يليه يمثل مستطيل مساحته : (2 × 3 )
والدور الذي يليه يمثل مستطيل مساحته : ( 3 × 4 ) وهكذا
اذن المطلوب معرفة مجموع الطبقات أي:
مج 1×2 + 2 × 3 + 3 × 4 + ......... + ن ( ن+ 1 )
مج ن ( ن + 1 ) المطلوب
= مج ( ن2 + ن )
= مج ن2 + مج ن
= ن ( ن+1 )( 2ن+1 ) /6 + ن(ن+1 ) /2
= [ ن ( ن+1 ) ( 2ن+1 ) + 3ن(ن+1 ) ] /6
= ن ( ن + 1)( 2ن +1 + 3 ) /6
= ن ( ن +1 ) ( 2ن + 4 ) /6
= 2ن ( ن+1 ) (ن + 2 ) /6
= ن (ن +1) (ن +2 ) /3
نشــاط:
الشكل التالي مكون من عدد من الطبقات :
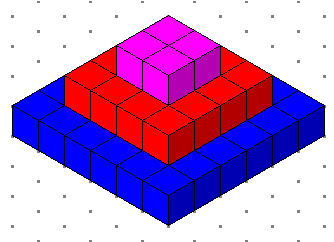
- ما عدد المكعبات اللازمة لبناء مثل هذا الشكل ؟
- كم مكعب نحتاج لإضافة بعض الأدوار الطبقات السفلية ؟
- ما مجموع المكعبات فى العشرة طبقات الأولى ؟
- ما القاعدة العامة التي تحدد عدد المكعبات في الطبقة الاولى ؟
من الشكل نلاحظ بان الطبقة العلوية مكونة من عدد المكعبات (4)
والدور الدي أسفل منه مكون من ( 16 ) مكعب
أي أن الأول يمثل : 2تربيع
والدور الثاني يمثل : 4تربيع
الثالث يمثل 6 تربيع
الأعداد نمطها 2 تربيع 4 تربيع 6 تربيع 8تربيع ........
الحد العام ( 2ن ) تربيع
فالحد العاشر تكون فيه ن=10 وعدد المكعبات في الدور العاشر =20 تربيع = 400 مكعب
نشــاط:
لاحظ الشكل المرسوم فى الصفحة التالية
- هل يمكنا معرفة كم مكعب نحتاج لرسم الحد العاشر
- ما هى القاعدة العامة التي تحدد عدد المكعبات اللازمة لبناء الحد الثاني ؟
تدريــب :
لاحظ الشكل المرسوم
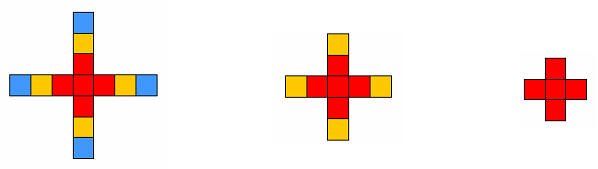
وأرسم الحد الذي يليه مباشرة
- كم مربعا نحتاج لبناء الحد العاشر من هذا الشكل ؟
- ما القاعدة العامة التى تحدد عدد المكعبات لبناء الحد النوني للشكل ؟