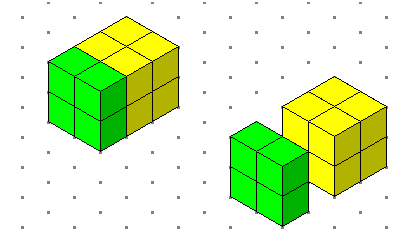
التحليــل إلى عوامـل
المقصود بتحليل العبارات الجبرية هو تحويلـها الى مقادير أخرمضروبة ببعضها أي ان تحليلها إلى عوامـل بإيجـاد العامـل المشـترك وتوضيح معــنى العامـل المشـترك أو باستـخدام المتطابقـات الأسـاسيـة
وهذا يتطلب دراسة العبارة الجبرية ، ومعرفة تراكيبها
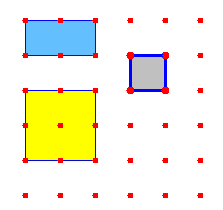
ولتوضيح ذلك نستخدم المكعبات باعتبار ان (س ) يمثل سطح مستطيل حد بعديه مكعبين اثنين والبعد الآخر مكعب واحد كما في الشكل 2 ×1
ويمكن تمثيل س2 يمثل بسطح المربع (س2) وتمثيل ( ص) بمربع ( 1× 1) كما في الشكل التالي:

وإعطاء الأنشطة المتعددة للتطبيق :
3 س2 +2 س
حيث تم بجميع المقدار بأخذ العامـل المـشترك ويمثل في صورة مستطيل مساحته الطول × العرض
من هنا تستنتج التلميذة معنى أخذ العامل المشترك
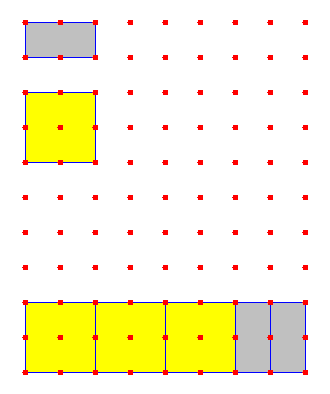
فيكون 3س2 +2س = س( 3س +2)
ويمكن أن يطبـق ذلك على الأنشطة الباقية
س2 + 2 س على النحو التالي:
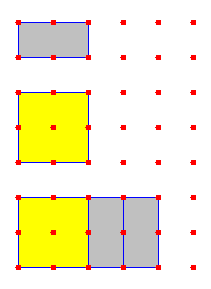
والمقدار س2 + 3س ص + يمكن تمثيله بالطريقة نفسها على النحو التالي:
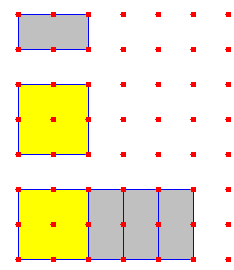
والمقدار س ص + 2 ص2 يمكن تمثيله على النحو التالي :
وبالطرية نفسها يمكن تمثيل المقدار س2+3س
ص+ص2 كما في الشكل التالي واعتبار المربع  = ص
2:
= ص
2:
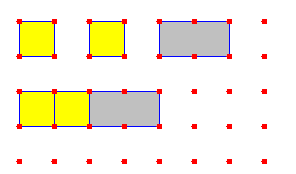
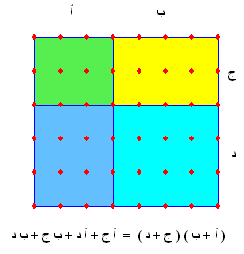
والتحليل معناه تحويل المقدار الجمعي الى مقدار ضربي بتحويل القطع مجتمعة الاى مستطيل كما في الشكل التالي:
ويكون بهدا المستطيل = ناتج التحليل أي أن
س2+3س ص+ص2 = ( س+2ص)(س+ص) وبالطريقة نفسها يمكن تحليل المقدار التالي :
2س2 ص + ص2 س
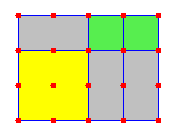
ويمكن كذلك تحليل مقادير من الدرجة الثالثة فالمقدار س3 + 2س2 ص+ ص2 س
يمكن تمثيله بمكعب طول ضلعه س= مكعبين على سبيل المثال والقطعة س2ص بقطعة على شكل موشور قاعدته مربعة مساحتها س2 وارتفاعها ص ( مكعب واحد)
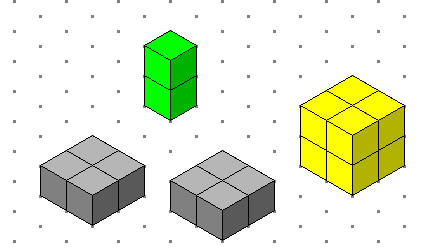
والتحليل كما تعلما تحويل القطع مجتمعة إلي جسم واحد كما في الشكل التالي
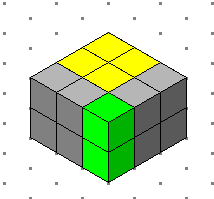
حاصل ضرب أبعاد المجسم( حجم المجسم) هو ناتج التحليل أي أن:
س [ (س +ص )2]
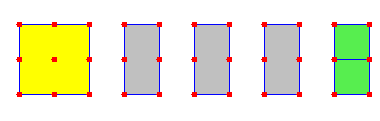
كما يمكن تحليل المقدار س3 + س2 ص = س2 ( س + ص )
كما هو موضح في الرسم

تـدريب:
توضيح ضرب قوسين
(أ+ ب) (حـ +د) = أحـ + أد +ب حـ +ب د
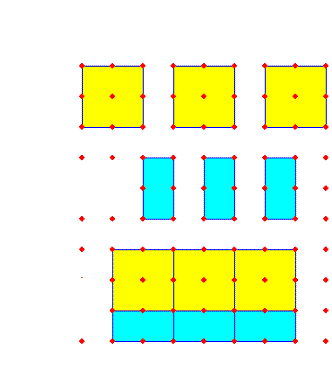
والمقدار 2ص2+س ص يمكن تحليله كما في الشكل التالي:
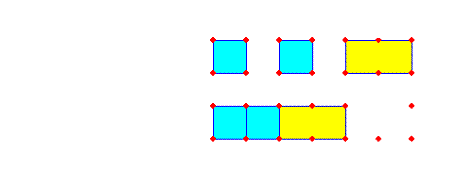
وبالطريقة نفسها يمكن تحليل المقدار 2س2ص+س ص2
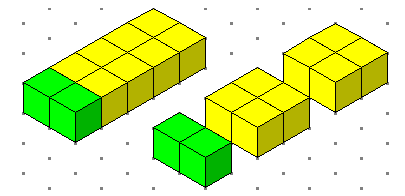
والمقدار س3+س2ص