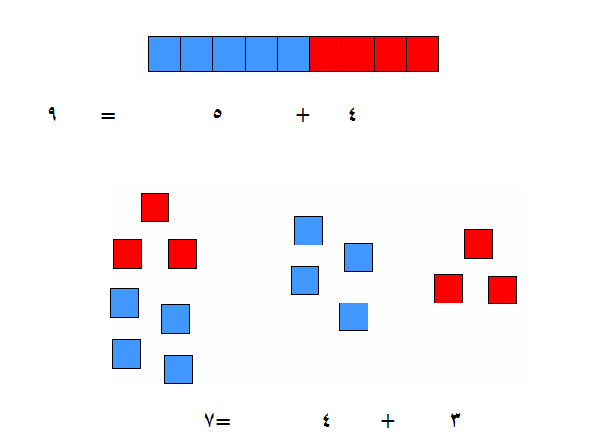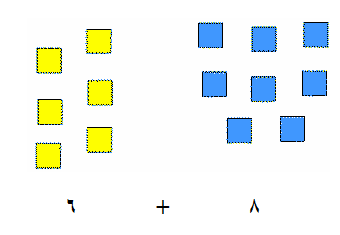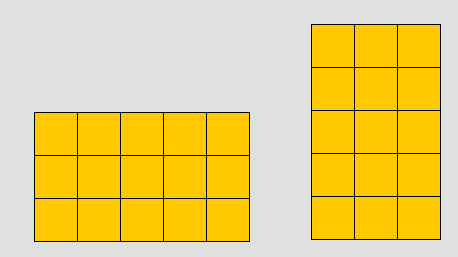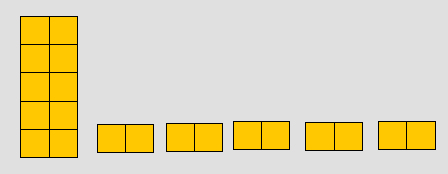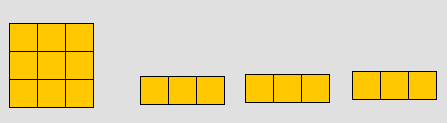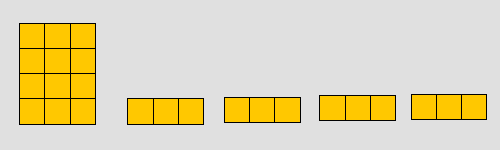العمليات الحسـابية الأساسية
(الجمع - الطرح -الضرب - القسمة )
عمليتي الجمع والضرب والعمليتين العكسيتين لهما الطرح والقسمة تسمى هذه بالعمليات الأربع ( العمليات الأساسية ) وذلك لأنها تشكل أساس دراسة الرياضيات في المرحلة الابتدائية والمراحل اللاحقة لها
ويتعرف من خلالها على الإشارات
( + ) تعنى الجمع أو زائـد
( - ) تعني الطرح أو ناقص
( × ) تعني الضـرب أو في
( ÷ ) تعني القسمة أو على
ولابد أن نحتاج إلى أن تفهم التلميذات الأفكار التي وراء تلك العمليات ولا يقتصر على إجراء تلك العمليات ، لأنه يمكن أن تجري التلميذة عملية الجمع ولكن ليس ذلك دليلا على فهم الجمع
فتقديم عملية الجمع والطرح على أنها إتحاديين لمجموعات منفصلة ، تتعرف التلميذة من خلالها على عملية الجمع وبنفس الطريقة ، يمكن للتلميذة أن تعرف عن طريق الفرق بين المجموعات المنفصلة على عملية الطرح وتعرف الطرح على انه العملية العكسية لعملية الجم ومن الوسائل المفيدة في ذلك التي تساعد على تطور استيعاب التلميذ لمفهوم عمليتى الجمع والطرح هو استخدام المكعبات المتداخلة ، لأنه من خلالها يستطيع التلميذة أن تفهم عملية الترابط بين المجموعات بشكل محسوس عند عرض المعلمة لها ذلك وتوضيحه ويجب أن تعطي تعريفا لكل عملية تجريها وعلى التلميذة أن تتعرف على عناصر كل عملية
الجمع
يكون عند إضافة كمية إلى كمية أخرى من إعداد أو أشياء على أن تكون من نفس النوعية ، فنكون قد جمعنا عددين أو شيئين
وكمثال عند إضافة مجموعة من المكعبات إلى بعضها فهذه طريقة سهلة ومباشرة وتوضح للتلميذة ذلك بشكل مباشر
درس الجمع
( الصف الأول الابتدائي )
الأهــداف :
- أن تربط التلميذة اتحاد مجموعتين منفصلتين بعملية الجمع
- توضيح مفهوم الجمع وربطه بمعني إضافة عدد إلى عدد
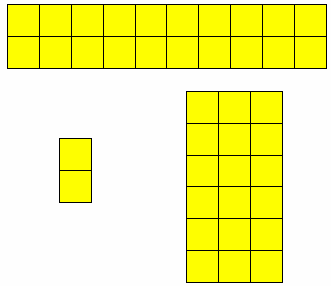
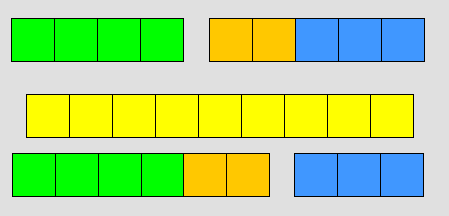
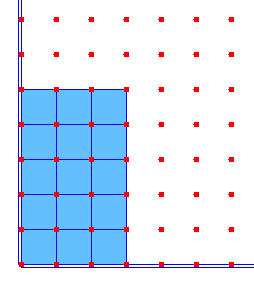
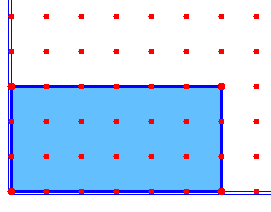
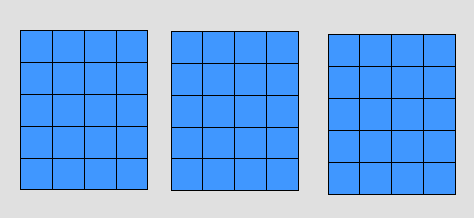
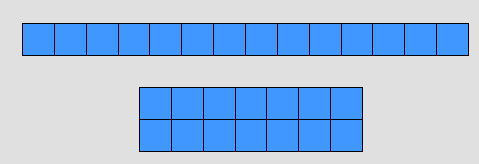
يعطي للتلميذ مجموعتين من المكعبات ، المجموعة الأولى تحتوي على (3) مكعبات والمجموعة الثانية تحتوي على (4) مكعبات ، ويطلب منها أن تضعها في مجموعة واحدة ، وهو لديه فكرة العدد فيجمعها فيكون لديه (7) مكعبات كما هو موضح في الرسم التالي
وكذلك إن تتعرف على كتابه الجمل : أ + ب = جـ
حيث ( أ ) المجموعة الأولى ، ( ب ) المجموعة الثانية ، (جـ ) ناتج الجمع 0
وهنا كذلك الهدف هو أن تتعرف التلميذة على الإشارات (+) و ( - ) و( = ) والتمييز بينها
الطرح
( الصف الأول الابتدائي )
الأهـــداف :
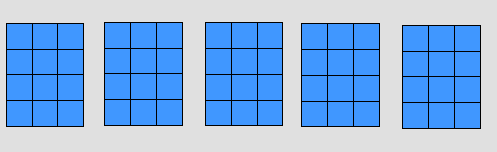
استعمال الطرح لكي توصف التلميذة عملية إكمال مجموعة لتكافيء مجموعة تم توزيع على التلميذات مجموعات مختلفة العدد من المكعبات المتداخلة ، بحيث لا يزيد عدد المجموعة الواحدة من (9) عناصر ، وهنا تبدأ التلميذة مقارنة عدد عناصر مجموعتها مع عدد عناصر مجموعة زميلتها
وتبدأ المعلمة بطرح الأسئلة على التلميذات بحيث توضح المجموعات ذات العناصر الأقل على عدد عناصر المجموعة التي تلزم للحصول على مجموعة عدد عناصرها يساوى عدد عناصر مجموعة زميلتها
وذلك يطرح السؤال : كم يلـزم ؟ وكم تحـتاج ؟
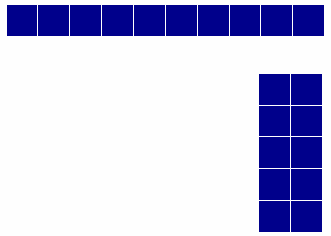
- مثلا : إذا كان لدى التلميذة الأولى مكعبين فيسأل عن كم يلزمها ليكون العدد (7) فهنا يضيف من زميلها (5) مكعبات فيصبح 7 - 2 = 5
ويوضح ذلك الرسم التالي:
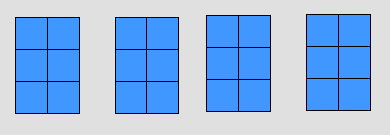
7 - 2 = 5
9 - 5 = 4
9 - 6 = 3
كامل الشكل
ناقص الشكل
الباقي من الشكل
حقائــق الجمع والطرح
لتعليم حقائق الجمع والطرح هناك طرق كثيرة
لكل حقيقة جمع يمكن أن تربط بينها وبين حقيقة الطرح
فمثلا حقيقة الجمع كما يتم شرحها في درس : حقائق الطرح في الصف الثاني الابتدائي
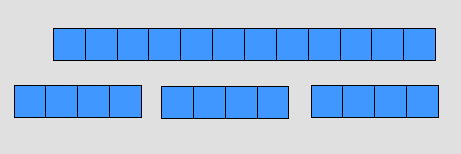
8 + 6 = 14 ،
كما في الرسم في الصفحة التالية :
يمكن أن نربطها بحقيقة الطرح : 14 - 6 = 8
المطروح و المطروح منه و الباقي 0 ويمثل العلاقة
المطروح + الباقي = المطروح منه
المطروح منه - الباقي = المطروح
وكذلك 14- 8 = 6 وهي ما يكون في مستويات متقدمة في الصف الرابع الابتدائي ما يتعرف عليه التلميذة
14 - 8
خواص الجمـــع
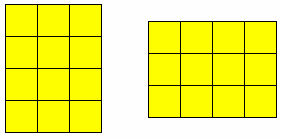
نستطيع اختصار حقائق الجمع وذلك بان تطبق بعض خواص الجمع ، ومن أشهر هذه الحقائق خاصية الترتيب ، خاصية التبديل في الجمع
يعـني ذلك أن ترتيب المجاميع لا يؤثر على نتائـج الجمع 0 وهو ما يعبر عنه بالشكل التالي :
حيث أ تمثل مجموعة من المكعبات ، وب مجموعة من المكعبات 0
فان : أ + ب = ب + أ
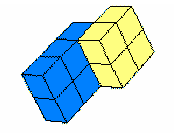
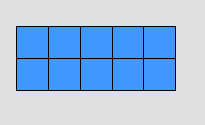
- مثلا : أ يمثل 4 مكعبات ، ويضاف إليها 3 مكعبات 0
4 + 3 = 7
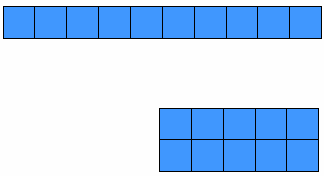
وإذا تم جمع 3 مكعبات مع 4 مكعبات كان الناتج نفسه 7 مكعبات اى3 + 4 = 7 وهكذا إذا أعطيت أمثلة متعددة 0 كما في الشكل التالي:
فهنا تستطيع التلميذة أن تميز بان جمع عدد بترتيب معين سيكون له نفس الناتج إذا أبدلنا الترتيب 2+3=3+2 كما في الشكل التالي
التجميع في الجمع:
هناك خاصية أخرى للجمع وتسمى التجميع في الجمع ونعبر عنها كالتالي :
أ و ب و جـ ثلات مجموعة من المكعبات الملونة حيث كل حرف يمثل عدد معين من هذه المكعبات كالتالي :
( أ + ب ) + جـ = أ + ( ب + جـ )
وتستعمل هذه الخاصية عندما يراد جمع أكثر من عددين ، يعطى في الصف الثاني الابتدائي درس التجميع
مثال : -
( 3 + 2 ) + 4 ـــ إعادة تسمية
3 + 2 + 4 = ـــ جمع
3 +( 2 + 4 ) = ـــ إعادة تسمية
أذن يمكن القول بان الجمع والطرح يمثلان نصف العمليات الأساسية ، لهذا لابد أن يتم تقديمها بشكل كبير في المرحلة الابتدائية ، وان يتم في مراحل
الضـرب :
تعتبر عملية الضرب أسرع طريقة لجمع أعداد متساوية ، فيمكن النظر إليها على إنها عملية جمع مكرر لمجموعات جزئية متكافئة 0
- مثلا : 2 + 2 + 2 = 6
فيمكن التعبير عنها 2 × 3 = 6 أي أن العدد 2 مكرر ثلاث مرات
أو أن الثلاثة مكررة مرتين 3 × 2
ويكن تمثيلها بالمكعبات المتداخلة حيث يوضح للتلميذة معنى الضرب عن طريق الجمع المكرر فهنا ليس من الضروري الترتيب ، مما سبق يمكن أن نقول بان :
2 × 3 = 3 × 2 = 6
أي أن 2 صفوف × 3 أعمدة أو 3 صفوف × 2 أعمدة وهذا ما يطلق عليه الابدال في عملية الضرب
ومن المهم تمثيل العدد الاول على محور السينات والعدد الثاني على محور الصادات
وهو ما يعبر عنه بالعلاقة أ × ب = ب × أ 0
ومن الأمثلة على ذلك : 3 × 5 = 5 × 3 = 15
المهم تمثيل العدد الاول على محور السينات والعدد الثاني على محور الصادات
ملحوظــة:
وهذا يدرس في الصف الثاني الابتدائي0
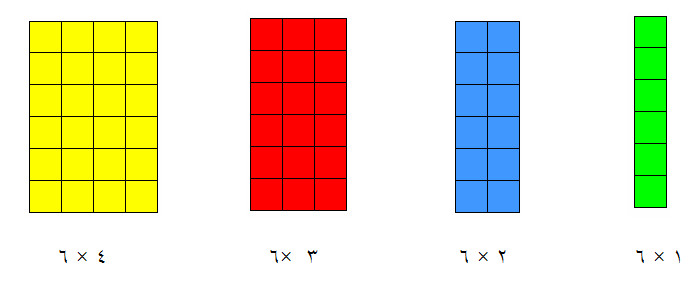
وتعطى كذلك ضرب الستة في الصف الثالث الابتدائي 0 فالهدف منه توضيح
عن طريق العدد 6 استنتاج جدول الضرب للعدد 6بحيث يكون ستة ستة وهكذا
فهنا يطلب من التلميذة أن يقوم ببناء ست مكعبات ، وتكررها كمجموعات كل مجموعة من ست مكعبات
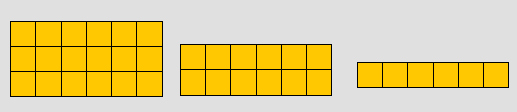
- فيكون المستطيل الأول 6 × 1
وبعد ذلك تضيف الى المستطيل الاول المستطيل الثاني المكون من ست مكعبات فيصبح مستطيل : 6 × 2 وهكذا0
- ويكون الشكل التالي عبارة 6 × 3
الشكل التالي يوضح 6 في واحد و ستة في اثنين و ستة في ثلاثة
فهنا يوضح للتلميذة جدول الضرب الخاص بالعدد 6 وبالتالي يمكن أن يكمل الاعداد
2 + 2 + 2 + 2 + 2 = 2 × 5
3 + 3 + 3 = 3 × 3
3 + 3 + 3 + 3 = 3 × 4
الإبدال في الضرب أ × ب = ب × أ
2 × 4 4 × 2 4 × 3 3 × 4
2 × 6 6 × 2 5 × 3 3 × 5
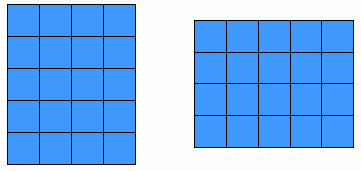
5 × 4 4 × 5 3 × 6 6 × 3
على اعتبار ان العدد الأول يمثل على المحور السيني والعدد الثاني على المحور الصادي
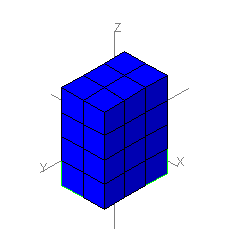
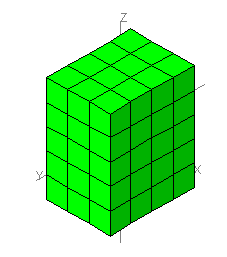
ضرب أ × ب × ج
من المهم جدا ان يمثل العدد الأول على محور السينات X والعدد الثاني على محور الصاداتY والعدد الثالث علي محور الإرتفاع Z
الشكل التالي يمثل 2 × 3 × 4
الشكل التالي يمثل 3 × 4 × 5
- وهناك خاصية أخرى للضرب وهى التجميع كما سبق وذكرنا في ( الجمع أي تحقيق العلاقة ) أ × ب × جـ = ( أ × ب ) × جـ = أ × ( ب × جـ)
معنى أ × ( ب × جـ) = ( أ × ب ) × ج
يمكن النظر للعدد الأول أ المنفرد وهو العدد الخارج من القوسين في الطرف الأيمن على أنه عدد المرات التي يتكون منها شكل بعداه ( ب × جـ) على النحو التالي:
على افتراض أن المقدار أ × ( ب × جـ) عبارة عن 3 × ( 4 × 5)
بالطريقة نفسها يمكن اعتبار الحد المنفرد وهو العدد الخارج من القوسين هو عدد المرات التي يتكون منها الشكل ببعديه . فالطرف الأسير من المقدار
أ × ( ب × جـ) = ( أ × ب ) × ج
يمكن النظر اليه على أنه شكل بعداه ( أ × ب ) مكرر ج مرة
وعليه فالمقدار أ × ( ب × جـ) فيه أ= 3 ب= 4 ج=5 يمكن تمثيله على النحو التالي
والتصغير للإيضاح فقط ويمكن توضيح المقدار بالمكعبات بدلاً من المربعات على النحو التالي
والطرف الآخر يمكن تمثيله على النحو النالي
والتصغير للإيضاح فقط
مثال لآخر
أ × ( ب × جـ) = ( أ × ب ) × ج
أ= 4 ب= 2 ج = 3
المقدار أ × ( ب × جـ)
4 × ( 2 × 3) يمكن تمثيله على أنه شكل بعده الأول 2 والبعد الثاني 3 مكرر 4 مرات على النحو التالي
المقدار ( أ × ب ) × ج
( 4 × 2 ) × 3 يمكن تمثيله على أنه شكل بعده الأول 4 والبعد الثاني 2 مكرر 3 مرات على النحو التالي
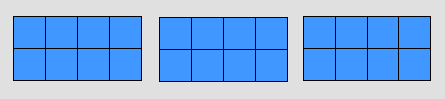
* - القســمة :
القسمة هي عملية تجزئة المقدار إلى أجزاء متساوية و عملية القسمة هي العملية العكسية لعملية الضرب . فقسمة 12 على 4 يمكن تمثيلها في مجموعات كل مجموعة مكونة من أربع مكعبات على النحو التالي وهي إجابة عن السؤال التالي كم أربعة موجودة في العدد 12؟
ويمكن استخدام فكرة توزيع العدد المقسوم 14 في شكل مستطيل أحد بعديه يكون المقسوم عليه 7 بعد ترتيب المقسوم يكون البعد الثاني للمستطيل خارج القسمة والشكل التالي يوضح قسمة 14 على سبعة
ويمكن كذلك أن تكون طريقة التقديم أن يستخدم التلميذات 10 مكعبات ويطلب من إحداهن تقسيمها بالتساوي على 5 تلميذات اخريات فتبدأ تعطي كل تلميذة واحد مكعب ، تجد نفسها انه يمكن القيام بالعملية مرة أخرى بذلك تكون قد أعطت كل تلميذة 2 مكعب على النحو التالي
أو استخدام فكرة تكوين مستطيل من العدد المقسوم بحيث يكون المقسوم عليه البعدالأول ( الممثل على المحور السيني ) من المستطيل على النحو التالي
أما قسمة 10 على 2 فيمكن تمثيها بالطريقة نفسها على النحو التالي
فهنا يوضح للتلميذة عناصر عملية القسمة
المقسوم المقسوم عليه ( القاسم ) خارج القسمة
10 ÷ 2 = 5
فقسمة 10 على 2 يكون الناتج 5 كما في الشك التالي:
وقسمة 10 على 5 ممثلة بالشكل التالي:
وقسمة 8 على 2 ممثلة بالشكل التالي:
إن ربط الضرب بالقسمة عن طريق توزيع العدد المقسوم في شكل مستطيل أحد بعديه العدد المقسوم عليه و البعد الثاني للمستطيل هو خارج القسمة كما سبق أن أوضحنا فإنه يكون لدى الطلاب الوعي بالعلاقة بين الضرب والقسمة ويمكن تدريس ذلك في الصف الرابع الابتدائي
و يمكن تمثيل القسمة مع باقي بالطريقة نفسها
مثال : أوجد ناتج قسمة 17 ÷ 3 ويتم توضيح ذلك باستخدام المكعبات المتداخلة ( الملونة )على النحو التالي :
حيث جعلنا المقسوم عليه 3 أحد بعدي المستطيل وقمنا بتوزيع المكعبات فكان الناتج 5 وبقي مكعبان
- يوضـح للتلميـذات عند قسمة 11 على 3تقوم بعمل مجموعات بحيث تحتوى كل مجموعة على 3 مكعبات ونجد انه يوجد 3 مجموعات ويتبقى لدينا 2 مكعب لا يمكن دخولها في المجموعة فيمثل هذا الباقي
فيكون (11 = المقسوم) و (3 =المقسوم عليه ) و ( 9 خارج القسمة) و(العدد 2 يسمى الباقي) وذلك يوضح في الرسم التالي:
11
11 ÷ 3

المقسوم =المقسوم عليه × خارج القسمة + الباقي
قسمة تسعة على أربعة يمكن تمثيلها بالشكل التالي:
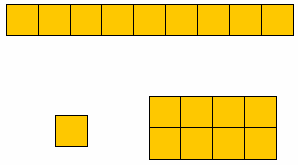
خارج القسمة= 2 والباقي 1
وقسمة 20 على 6 يكون الناتج 3 والباقي 2 كما في الشكل التالي
وقسمة 20 على 3 يكون الناتج 6 والباقي 2 كما في الشكل التالي