|
المتطابقة هي مساواة بين عبارتين رياضيتين متكافئتين "
خير أداة لتمثيل المتطابقات هو معمل الجبر على الرابط التالي
ويمكن باستخدام المكعبات المتداخلة
او اللوحة لهندسية، توضيح وإيجاد مفكوك
المتطابقات بطريقة ملموسة للتلميذات 0
أولا :
مربع مجموع حدين : ( س + ص ) 2
يمكن تقديم المفهوم بأرقام أولا حيث يمكن طرح السؤال التالي
كيف يمكن ثمثيل
المقار التالي بالمكعبات
( 3 + 2 ) 2
من خلال الممارسة يعرف الطالب تمثيل
( 3 + 2 ) على النحو التالي
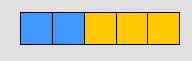
كما يعرف تمثيل 3 تربيع و اثنين تربيع على
النحو التالي
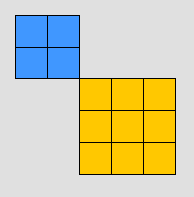
كما يعرف الطلاب ان
(
3 + 2 ) 2 عبارة عن مربع وعليهم اكمال المربع ولكن بلون
مختلف على النحو التالي

ما طول المستطيل وعرضه وما علاقة بعدي
المستطيلين بالعددين الأساسين
نحن نعلم ان مساحة الشكل الكلي= مساحة الأجزاء
المتكونة منه
( 3 + 2 ) 2 = 3
تربيع + 2 تربيع + 2×
3×2
عند تبديل الارقام بالرموز نعتبر ان
س هي الحد الأول ، ص هي الحد الثاني ، وأن (س + ص) هو
مجموع الحدين
حيث س يمثل بثلاث مكعبات ، ومقدار ص بمكعبين
اثنين
فيكون ( س + ص )2
عبارة عن مربع طول ضلعه ( س + ص )
1- توجد مجموع أجزاء الشكل كما هو موضح في الخطوة الثانية 0
2- الأجزاء هى : ( س2 + ص 2 + س ص + س ص )
فيكون ( س + ص )2 = ( س2 + 2س ص + ص2 )
|
مربع مجموع حدين = مربع الحد الأول + ضعف الحد الاول × الحد الثاني +
مربع الحد الثاني
|
| |
أما معمل الجبر فيكمن استخدامه لتحديد
بعد المربع الأساسي واكماله بالقطع على النحو التالي
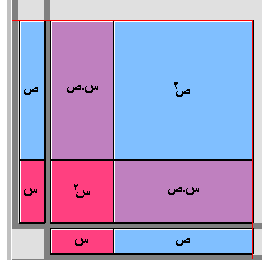
ويمكن
للوحة الهندسية ان تقوم بالدورنفسه على النحو التالي
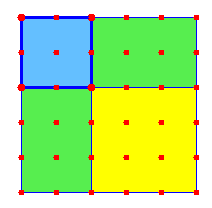
او يكون تمثيل (س+1)2 بالطريقة نفسها على اعتبار أن س=2
و ص= 1
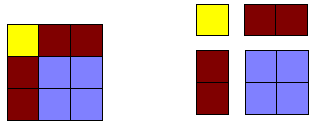
( س + ص ) 2
س + ص
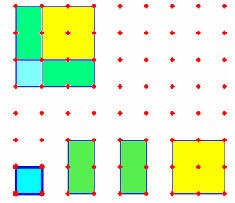
س 2 + 2 س ص + ص 2
ثانيا :
الفرق بين
مربعين س2 - ص2
لإيجاد مفكوك المتطابقة نقوم بالخطوات
التالية :
البدء بالمحسوس وترجمة المفهوم الى ملموس على النحو التالي
بداية لدينا ارض مربع الشكل نريد بناء غرفة مربعة الشكل في أحد
الأركان ما المساحة المتبقية بعد استقطاع الغرفة
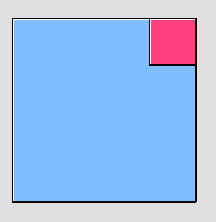
المربع الكبير طول ضلعه س و
مساحته س تربيع مساحته
الغرفة المستقطعة منها طول
ضلعها ص ومساحتها ص تربيع
المساحة المتبقية بعد بناء
الغرفة = س تربيع - ص تربيع
المساحة التبقية هي كما في
الشكل التالي
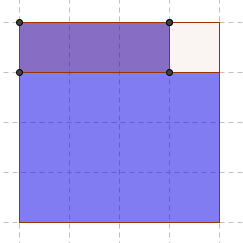
طول المربع الكبير س تم
اقتطاع جزء مقداره ص مساحة الجزء المتبقي = س - ص
بقطع المستطيل العلوي اللي
احد بعديه س والآخر س - ص ثم لصقه بجوار المستطيل السفلي
اللي طوله س ليصبح الطول الجديد = س+ ص على النحو التالي
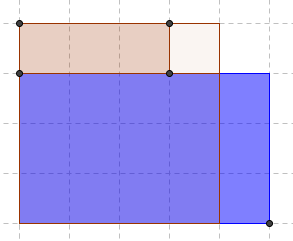
وبالتالي
يكون س2 - ص2 = (س - ص )(س +ص)
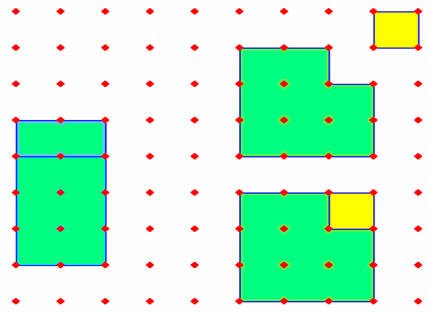
ويمكن شرح المفهوم باللوحة الهندسية على النحو التالي :
- عمل مربع كبير مساحته س2
- يحدد مربعا صغير مساحته ص2 ، وليكن مكعب واحد ويتم حذفه من
المربع الكبير
- يتم حذف الجزء الأسفل من المربع الذي مساحته : ص ( س- ص )
ونضعه بمحاذاة الجزء الآخر 0
- ينتج مستطيل بعداه ( س - ص ) و ( س + ص )
فيكون ( س+ ص ) ( س- ص ) = س2 - ص2
|
استنتاج :
|
|
حاصل ضرب مجموع حدين بالفرق بينهما=مربع الحد الاول-مربع الحد الثاني
|
متطابقة مربع الفرق بين حدين
( س- ص ) 2
نبني
مربع كبير بطول س ونرسم داخله مربع صغير بطول ص فتكون مساحة
المربع الصغير الأحمر هي ( س - ص )2 التي نريد حساب مساحته

بالطبع المساحة المطلوبة تساوي مساحة المربع الاساسي س2 ناقص
الاجزاء الباقية التي باللون الأزرق وهي المستطيل الأزرق
العلوي ومساحته = س ص + المستطيل اللي على يمين
اللي على يمين المربع الأحمر و مساحته = ص ( س- ص)
( س - ص )2 = س2 - {( س ص +
ص(س-ص) }
= س2 -{س ص + س ص - ص2}
= س2 - س ص - س ص + ص2
= س2- 2 س ص + ص2
|
استنتاج :
مربع الفرق بين حدين = مربع الحد الاول - ضعف(الحد
الاول × الثاني ) + مربع الحد الثاني
|
رابعـا : -
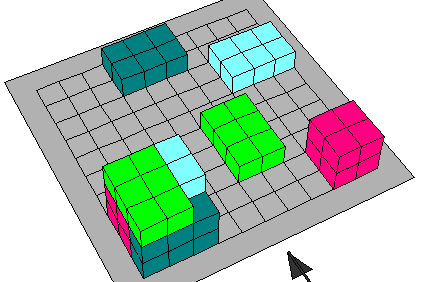
مكعب مجموع حدين ( س + ص ) 3
حيث ان س الحد الاول ، ص الحد الثاني ،
(س+ ص) مجموع الحدين0
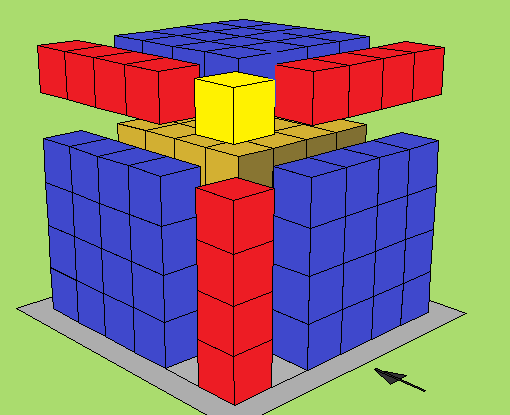
الحجم الاجمالي للمكعب المكون حرفه من قطعتين
الاولى الحمراء س والأخرى الصفراء ص اي ان طول حرفه= (س+ص )
وحجمه هو:
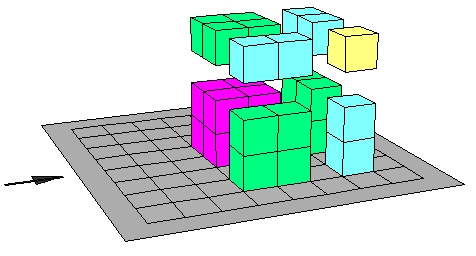
( س +ص )3 = حجم االأجزاء المكونة للمكعب
= حجم الثلاث القطع الزرقاء + حجم الثلاث قطع الحمراء + حجم
القطعة الصفراء +حجم القطعة المكعبة الشكل البرتقالية
= 3 س2 ص +3 س ص2 +ص3 + س3
= س3 + 3 س2ص +3 س ص3+ص3
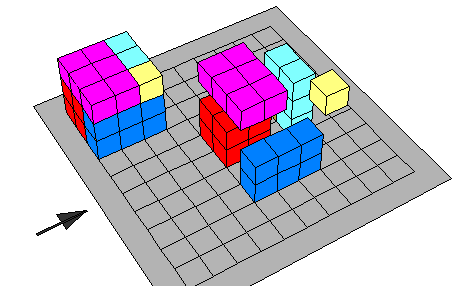
لتوضيح مفكوك مكعب مجموع حدين ( س + ص)3 نقوم بما يلي :
- بناء جسم من مكعبات س يمثل في صورة ( س + ص )3
أى يكون بعد المكعب ( س + ص)
حجمه = (س + ص) (س +ص ) (س +ص )
- نقوم بتجزأة المكعب إلى الأجزاء المطلوبة كما في الخطوات السابقة 0
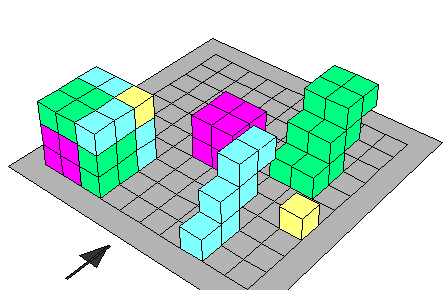
- الشكل الأول س3 ويقطع من الجسم 0 فيبقي الشكل الذي أبعاده س و س و
ص أي س2 ص
- ويمثل 3 قطع إذن 3 س2 ص 0
- وكذلك الجزء الآخر الذي أبعاده ص وص و س يمثل س ص2
ومكون من ثلاثة قطع أى 3 س ص2
- إذن ( س +ص )3 = س3 +3س2ص + 3 س ص2 + ص3
ويمكن أن يكون على الصورة :-
(س +ص )3 = س3 + 3س ص ( س+ ص ) + س3
تدريـب :
أوجد مفكوك ( س + 2ص ) 3
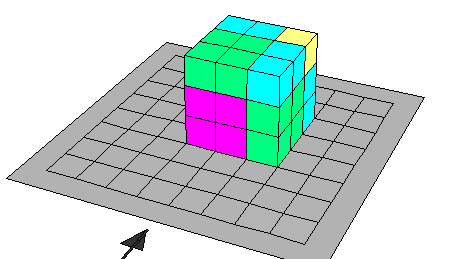
خامسـا :
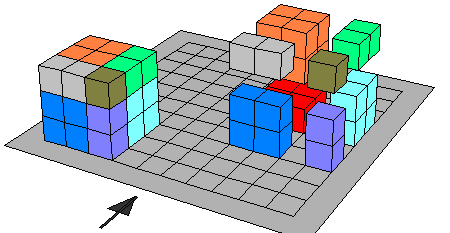
مكعب الفرق بين حدين : ( س - ص )3
حيث يمثل س الحد للاول ، ص الحد الثاني
(س -ص)3 = (س-ص) (س-ص) (س-ص) = ( س-ص)(س -ص)2
= (س-ص) (س2 -2س ص+ ص2)
= س(س2-2س ص+ص2) -ص(س2-2س ص+ص2)
= س3 -2س2ص+ س ص2 -ص س2 +2س ص2 -ص3
= س3 -3س2ص +س ص2 -ص3
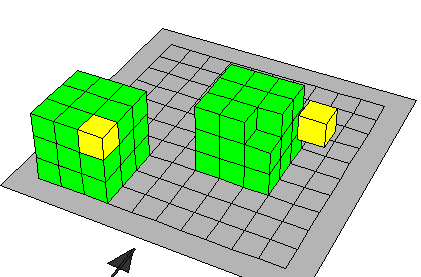
لبيان مفكوك مكعب الفرق بين حدين ( س -ص )3
- بناء مكعب يكون طول بعده س فيكون حجمه س3
- توجد المقدار ص3 حيث يمثل مكعب صغير بعده (ص )
- نقوم بطرح ص3 وبعض الأخرى من الجسم للحصول على ( س - ص)3
- يبقي لدينا من الأجزاء س2 ص ثلاثة اجزاء 0
وكذلك س ص2 ثلاثة اجزاء وهي على النحو التالي يمكن توضيحها:
3[(س-ص)2ص]و 3ص2(س-ص)
=3(س2-2س ص+ص2)ص -3س ص2 -3ص3
= 3س2ص-6س ص2+3ص3+س ص2-3ص3
=3س2 ص-3س ص2
ويمكن تمثيلها كذلك بالصورة :
(س -ص )3=س3 - 3س ص( س -ص ) - ص3
|
استنتاج : |
|
مكعب الفرق بين حدين = مكعب الأول - 3× الأول × الثاني × الفرق بين
الحدين - مكعب الثاني 0 |
سادسـا :
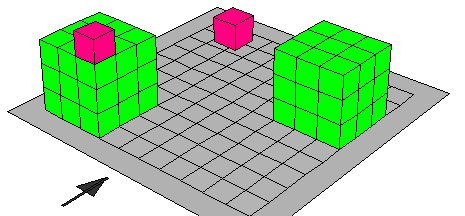
مجموع مكعبين ( س3 + ص3 )
حيث أن س يمثل الحد الأول ، ص يمثل الحد الثاني :
س3 +ص3 = (س + ص) (س2 -س ص +ص2 )
لايجاد مفكوك مجموع مكعبين نتبع الخطوات التالية :
- بناء مكعب صحيحة ( س3 ) كما هو موضح بالرسم حيث ابعاده س
- يضاف المكعب الصغير ص3 على المكعب س3
فيمثل الشكل س3 + ص3
- نحدد اجزاء الشكل المطلوب على النحو التالي :
- نقتطع الشكل الذي حجمه ص2 ( س + ص )
فك الجزء المتبقي واضافته
فيصبح حجمه س ( س- ص) (س+ص)
وبتجميع الشكل ينتج :
س3 +ص3 = ص2 ( س +ص ) +س( س2 -ص ) (س+ص )
= س ص2 +ص3 + س( س2 -ص2)
= س ص2 +ص3 + س3 -س ص2
=(س+ص ) (ص2 + س2 - س ص) = (س+ص) (س2 - س ص + ص2 )
|
مجموع مكعبين = ( مجموع الحدين ) ×( مربع الحد الأول ) - حصل ضرب
الحدين + مربع الحد الثاني ) |
|
|
|
سـابعا :
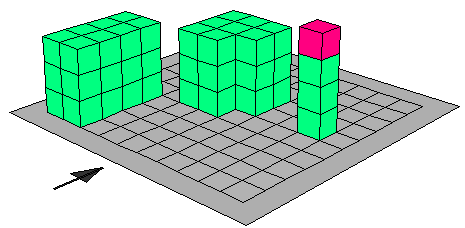
الفرق بين مكعبيـن : ( س3 - ص3 )
س3 -ص3 = ( س - ص) ( س2 + س ص + ص3 )
لايجاد المقدار ( س3 - ص3 ) نقوم بالخطوات التالية :-
- بناء مكعب حال بعداه (س) ، حجمه يصبـــح (س3 ) كما هو
موضح بالرسم 0
- تعيين المكعب (ص3 ) من المكعب الكبير الذي بعدد (ص) فيتكون لدينا الشكل
التالي :
- تحدد المقدار بتحديد الاجزاء له على النحو التالي :
الشكل الصغير حجمه ص 2 ( س- ص )
المتبقي من الشكل يتم ترتيبه بحيث يصبح حجمه :
س ص ( س- ص ) والجزء الآخر س2 ( س - ص)
- وبتجميع الشكل الناتج يصبح المقدار على الصورة 0
س3
- ص3 = ص2 ( س - ص ) + س ص (س- ص ) +س2 (س- ص )
=
(س -ص )
[
ص2 + س ص
+ س2 ]
=
( س- ص ) ( س2 + س ص + ص 2 )
ملاحظة :
توضح كذلك الاجزاء (س+ص ) (س-ص ) س =(س2 -ص2)س
لان (س2-ص2) س + ص2(س-ص) =س3-س ص2+س ص2-ص3 = س3-ص3
|
استنتاج : |
|
الفرق بين مكعبي حدين =( الفرق بين الحدين ) × ( مربع الحد الاول +
حاصل ضرب الحدين + مربع الحد الثاني ) |
|























