الهندســة

إن للهندسة دورا مهما في منهج الرياضيات بالمرحلتين الابتدائية والمتوسطة فهي من المجالات المهارية الأساسية التي يجب تنميتها لذا فانه من الجدير إن يحظى بمجال واسع وذلك بالانطلاق من المحسوس وتصور لهذا المحسوس كجسم هندسي

ويقول بياجيه " إن دراسة الهندسة ترتبط بدراسة كل البنيات الاساسية في الرياضيات وهذا يشكل صعوبة في دراستها ويكسبها في نفس الوقت أهمية كبيرة 0 وهى بالنسبة للطفل وليدة تجربته ويجب الاعتناء في المرحلة الأولى من التعليم الابتدائي بالناحية التجريبية التى تتطلب الممارسة العملية

وان ما يتضمنه منهج الرياضيات للهندسة هو التحويلات الهندسية ويتم تدريس ذلك عمليا من خلال قيام التلميذات بانشطة عملية يتعاملون بها مع أشياء ملموسة مثل المجسمات ومنها المكعبات المتداخلة

فيمكن تقديم بعض المفاهيم الهندسية للتحويلات بصورة هندسية فى المراحل الأولى

ومن هذه التحويلات : (التناظر - الانسحاب - الدوران - التشابه

إن التناظر حول محور يمكن تقديمه عن طريق الإنتساخ والطي ، وكي لا يكون تجريديا يتم عمله أمام التلميذات باستخدام المكعبات المتداخلة لتوضيحه

والتناظر هو التماثل أى إيجاد الشكل المطابق له تماما

فعرض التناظر يهدف منه أن تدرك التلميذة مفهوم التناظر حول محور وكذلك أن يمكن التلميذة من إيجاد نقل شكل نظير حول محور وهذه دروس تعطي في المرحلة الابتدائية في الصف الثاني الابتدائي

إدراك مفهوم التناظر ، في الصف الثالث الابتدائي

كذلك في المرحلة المتوسطه في الصف الأول والثاني

حيث تدرك التلميذة مفهوم التناظر بالطريقة المحسوسة حيث تقوم بنفسها بمقارنة القطعة مع نظيرتها

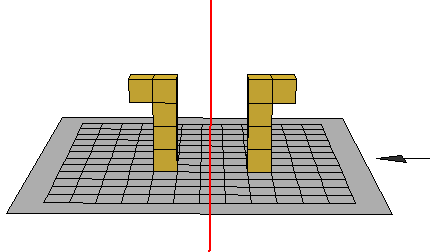
فأول مرحلة أن يقدم للتلميذة شكلان يكونان متناظران حول محور فتدرك التلميذة بان الشكل الأول ينطبق على الشكل الثاني

وان تكون المسافة بين الشكلين والمحور على نفس البعد من الشكلين

ويتم توضيح ذلك بالمكعبات كما في الشكل التالي

وبالمناقشة مع التلميذات يمكن الاستنتاج والتوصل إلى تعريف التناظر حول محور وهو:-

تعريف : إذا كان س ص هو المنصف العمودي للمسافة بين أ ، أً فان أً هي نظير للنقطة أ و س ص هو محور التناظر للنقطتين

ويمكن استخدام المرايا العاكسة لتوضيح فكرة التناظر

ثم نبدأ بعد ذلك بالمناقشة لاستنتاج خواص التناظر حول محور من خلال الأشكال التى تم إيجاد نظيرها بان:-

3- التناظر حول محور يحافظ على التعامد والزوايا

نتيجــة :

إذا انقلب الشكل حول خط فيسمى ذلك ( تناظر )

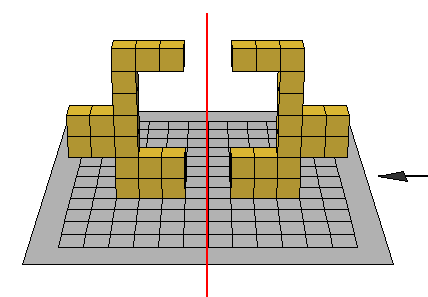
ويمكن استخدام المربعات الملونة لتميثل التناظر حول محور كما في الشل التالي :

الإنسحاب الإزاحة

هو نقل الشكل من مكان إلى آخر بجانب الشكل الأصلي ، أى هو تحريك الشكل بنفس الاتجاه وبنفس المسافة ، إلى أسفل أو أعلى أو إلى اليمين أو إلى اليسار ،

ويبقي الشكل كما هو ، ولكن في وضع مختلف ويعطى الدرس في المرحلة المتوسطة ( الصف الثاني المتوسط ) وكذلك في المرحلة الثانوية ( الصف الأول ثانوي )

والهدف أن تتعرف التلميذة على الانسحاب وما هيته واستنتاج خصائص الانسحاب من الشكل

ويمكن توضيح ذلك عمليا باستخدام المكعبات من قبل التلميذات والمعلمة حيث يتم تركيب شكل من المكعبات ويوضح على سطح مستوى وتتم إزاحة الشكل باتجاه معين وبمساحة معينة مثلا إلى اليمين أو إلى الأعلى ويمكن في اتجاهين اليمين وإلى الأعلى أو الأسفل وإلى اليمين وتحدد الشكل الناتج من الإزاحة فيكون نفس الشكل

ويوضح ذلك بالرسم في الصفحة التالية وخطوات الرسم فنحدد صورة كل نقطة على الشكل

ويمكن استنتاج خصائص الانسحاب من خلال العرض فنجد أنها تمثل نفس خصائص التناظر

ملاحظــة :

يمكن إثبات ان تركيب تناظرين حول محورين متوازيين هو انسحاب عن طريق الرسم في الصفحة التالية حسب الخطوات للرسم

نتيجــة :

إذا أزيح الشكل في خطوط مستقيمة يسمى ذلك ( انسحاب)

الـــدوران

يتم توضيح الدوران للتلميذات على انها تدوير الشكل حول نقطة معينة بمقياس محدد ( زاوية يعرف مقدارها ) في الاتجاه الموجب أو الاتجاه السالب

يدرس الدوران في مرحلة متقدمة المرحلة المتوسطة ( الصف الثاني متوسط )

وكذلك في الصف الأول ثانوي 0 بمرحلة متقدمة حيث تستخدم القوانين

ولكن لتوضيح معنى الدوران للتلاميذ بشكل ملموس ، وباستخدام المكعبات المتداخلة حيث تكون شكل يبنى بالمكعبات أى شكل ، وتقوم التلميذات بوضعه

على سطح مستوى ولإيجاد الدوران في أحد الاتجاهات وبمقدار محدد وليكن زاوية 90 درجة فينتج الشكل

كما هو في الرسم بالصفحة التالية :

ويمكن التوصل بالشرح والمناقشة إلى التعريف التال

يكون التحويل الهندسي دورانا إذا نتج عن تناظرين حول محورين متعامدين في م هى مركز الدوران زاويتة ضعف الزاوية بين المحورين

نتيجــة :

إذا دار الشكل حول نقطة فان ذلك يسمى " دوران " 0