المضــــــاعف
إن فكرة المضاعف يمكن ان تبدأ 0من جدول الضرب :مثلا جدول العدد 2 هو 2 ، 4 ، 6 ، 8 ، .......هى مضاعفات للعدد 2
وكذلك الأعداد 4 ، 8 ، 12 ، 16 ، ........مضاعفات العدد أربعة.
مضاعفــات الأعــداد
الأهــداف:
- إن يتعرف التلميذ على أن مضاعفات عدد هي حاصل ضرب العدد في الأعداد الصحيحة
- إن يوجد مضاعفات بعض الأعداد
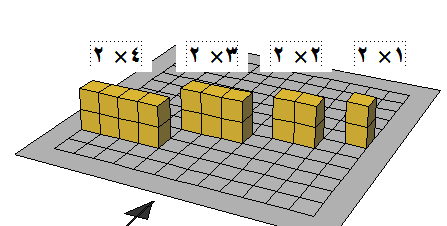
ويتم توضيح ذلك باستخدام المكعبات المتداخلة حيث يعطي للطالب مجموعة من المكعبات ويطلب منه بناء مستطيلات مختلفة الأبعاد على أن يكون أحد بعدى
كل مستطيل من مكعبين اثنين حيث نلاحظ ان الشكل الناتج لدينا من المستطيلات كما واضح في الرسم التالي

يتكون من المستطيلات التالية :
- مستطيل بعداه 2 × 2
- مستطيل بعداه 3 × 2
- مستطيل بعداه 4 × 2
مع التأكيد على تمثيل البعد الأول لكل شكل في الأسفلي والبعد الآخر في الأعلى ( فوق ) كما في الشكل السابق
وهكذا يكون ناتج الضرب مضاعفات للعدد
إذا أردنا حساب مضاعفات العدد 4 مثلاً فنحضر المكعبات المتداخلة بين التلميذات ويطلب تحديد مستطيل مكون من أربع مكعبات بحيث أحد بعديه العدد (1) والآخر (4) ثم نضيف إليه كذلك 4 مكعبات فيكون الناتج :
4 + 4 =8 مكعبات 0
وفي خطوة ثالثة نضيف 4 مكعبات تتكون :
4 + 4 + 4 = 12
نستنتج ان 4 ، 8 ، 12 000000 مضاعفات للعدد ( 4 )
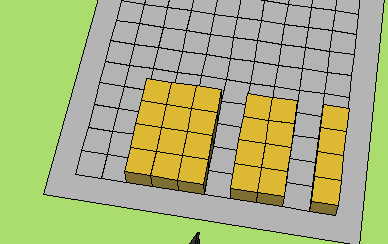
مع التأكيد على تمثيل البعد الأول لكل شكل على المحور السيني والبعد الآخر على المحور الصادي كما في الشكل أعلاه
المضاعف المشترك الأصغر لعددين
( الصف السادس الابتدائي )
وكذلك ( الصف الثاني المتوسـط )
تعلم الطالب كيفية حساب المضاعفات لعدد ، باستخدام المكعبات وسوف تتعلم الآن طريقة إيجاد المضاعف المشترك الأصغر لعددين
إذن الهدف معرفة المضاعف المشترك الأصغر لعددين ، وايجاده بكتابة سلسلة من مضاعفات العددين .
فيمكن تقديم ذلك باستخدام مسائل من الحياة اليومية مثلاً
مثال لدى محمد مبلغاً من المال يمكنه أن يختار بين أن يشتري بكامله أقلاماً أو مراسم على سبيل المثال وكان سعر القلم 4 ريال بينما سعر المرسمة 3 ريال فكم كان لدى محمد؟ وما أصغر تلك المبالغ التي تحقق الشرط؟ ( يمكنه من أن يختار بين شراء الأقلام أوشراء المراسم بكامل المبلغ)
يمكننا هنا بناء جدول يوضح المبالغ الممكنة التي تحقق الشرط وهو ان المبلغ يكفي لشراء أقلاماً أو مراسم على النحو التالي:
|
العدد |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
|
سعرالأقلام |
4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 | 44 | 48 | 52 |
|
سعرالمراسم |
3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 | 33 | 36 | 39 |
من الجدول نلاحظ أن هناك أرقاماً تحقق المطلوب وهي الملونة باللون الأحمر التي يمكن أن تمتد إلى أكثر من الموجودة في الجدول من مضاعفات كل من سعر القلم
ومضاعفات سعر المرسمة وهو إجابة السؤال الأول (فكم كان لدى محمد )
وهي المبالغ المسجلة باللون الأحمر في الجدول التالي:
| 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 | 44 | 48 | 52 |
تلك المضاعفات تسمى المضاعفات المشتركة بين العددين 3 , 4 وهي 12, 24, 36,.....,.....
ولكن السؤال كان أصغر تلك المبالغ التي تمكنه من الاختيار بين شراء الأقلام أو شراء الدفاتر؟
وعليه يكون أصغر مبلغ هو المضاعف المشترك الأصغر. ومن هنا جاءت تسمية المضاعف المشترك الأصغر.
يتضح لنا من الجدول أن أصغر تلك المبالغ التي تحقق الشرط هو 12 وهو الإجابة عن السؤال الثاني ( ما أصغر تلك المبالغ التي تحقق الشرط؟)
أصغر المضاعفات مشترك بين 4 , 3 هو 12
و يمكن استخدام المكعبات لتمثيل المسألة وذلك أن يطلب من التلميذات بناء سلسلة مكررة من 3 مكعبات( سعر المرسمة) وسلسلة مكررة من 4 مكعبات( سعر القلم )
ويتم وضعهما تحت بعض إلى أن تتساوى السلسلتان كما في الشكل التالي :
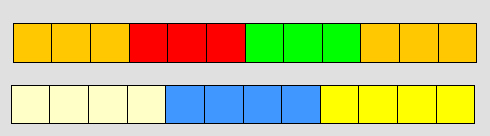
وبعد ذلك يتم متابعة مضاعفات كلا من العدد 3 والعدد 4 حتى يتساويان فنجد إن المضاعف الأصغر للعددين يمثل في العدد 12 مما يعني أن 12 ريال تمكننا من
شراء 3 أقلاام أو 4 مراسم
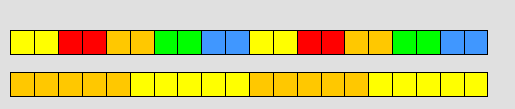
بالطريقة نفسها الشكل التالي يمثل المضاعف المشترك الأصغر للعددين 2 ,5
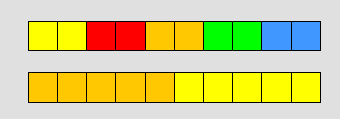
نلاحظ أنه بتكرار السلسلة نفسها نجدأكثر من مضاعف مشترك للعددين 2 و 5 ولكننا نبحث عن أصغر المضاعفات والشكل التالي يمثل مضاعف آخر للعددين 2 و 5
وبالطريقة نفسها يمكن حساب المضاعف المشترك الأصغر للعددين 4 , 6 و صياغة مسألة مشابهة للمسألة الأولى مع تغير في الأسعار فقط عن طريق ببناء سلسلة من 4مكعبات وأخرى من 6 مكعبات حتى تكون السلسلتان متساويتين على النحو التالي :
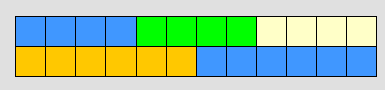
وعليه يكون المضاعف المشترك الأصغر =12
وبتكرار السلسلة الأولى في كل مرة نحصل على المضاعف التالي كما في الشكل أدناه مع ملاحظة تصغير الصورة فقط

وبطريقة الجدول السابقة يمكن حساب المضاعف المشترك الأصغر عندما يكون العددان صغيرين مثل 24,36 على النحو التالي
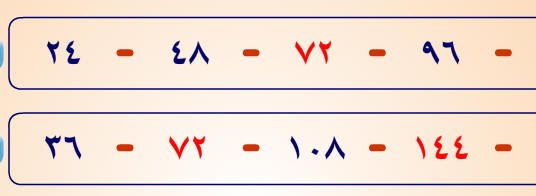
فالمضاعف المشترك الأصغر لهما هو 72 ويمكن أن يكون للعددين مضاعفات أخرى في حال اكملنا السلسلة على النحو التالي

صياغة تطبيق للمضاعف المشترك الأصغر
يمكن حل التطبيق التالي : شركة إنتاج البيض لديها نوعين من اللأطباق لبيع البيض فيها , النوع الأول يضم 24 بيضة بينما النوع الآخر يضم 36 بيضة . المطلوب
أولاَ معرفة عدد البيض الممكن وضعه بكامله( كل البيض) إما في النوع الأول أو النوع الآخر من الكراتين بدون أن يبقى من البيض شييء؟ وما هو أصغر عدد من البيض يحقق الشرط
فتكون إجابة السؤال الأول 72 بيضة أو مضاعفاتها 144 أو 216 وبالطبع إجابة السؤال الثاني هي 72 بيضة حيث يمكن وضع كل البيض في ثلاثة أطباع من النوع 24أوطبقين اثنين أطباق من النوع 36 أي 3 ×24=72و 2×36=72
هناك طريقة سهلة لحساب المضاعف المشترك الأصغر لعددين عنما يكون العددان صغيرين مثل 48 , 81 على النحو التالي
بالتحليل الشجري إلى العوامل الأولية على النحو التالي:
| العدد الأول | العدد الثاني |
|
|
|
|
العوامل الأولية هي : 2 ثلاث مرت و 3 مرتين |
العوامل الأولية هي: 2 مرتين و 3 و 7 |
| المضاعف المشترك الأصغر هو حاصل ضرب الأعداد الأولية المشتركة وغير المشتركة التي تظهر أكثر المرات عدداً | |
|
المضاعف المشترك الأصغر= 2 × 2 × 2× 3× 3× 7 = 504 |
|
|
القاسم المشترك الأكبر هو حاصل ضرب الأعداد الأولية المشتركة التي تظهر أقل المرات عدداً |
|
|
المضاعف المشترك الأصغر= 2 × 2 × 3=12 |
|
عندما يكون العددان كبيرين من الصعب استخدام التحليل الشجري فهناك طريقة أسهل وأسرع تعتمد على القواسم المشتركة بين العددين بدون شرط أن يكون القاسم المشترك عدد أولي
فالعددين 240 ,360 يمكن تحليلهما على النحو التالي :
| العدد الأول | العدد الثاني | يقبلان القسمة على |
| 240 | 360 | 10 |
| 24 | 36 | 6 |
| 4 | 6 | 2 |
| 2 | 3 |
ليس بينهما قاسم مشترك |
حاصل ضرب الأعداد الموجودة في العمود الأخير من الجدول = القاسم المشترك الأكبر للعددين = 10×6×2=120
المضاعف المشترك الأصغر= حاصل ضرب الأعداد الموجودة في العمود الأخير من الجدول × الأعداد الموجودة في الصف الأخير من الجدول شريطة عدم وجود عوامل مشتركة بينها
المضاعف المشترك الأصغر=120×2×3=720
-------------------
ويمكن حساب المضاعف المشترك الأصغر للعدين 72,84 حيث استخدمنا فيه التحليل الشجري لحله .
| العدد الأول | العدد الثاني | يقبلان القسمة على |
| 72 | 84 | 4 |
| 18 | 21 | 3 |
| 6 | 7 |
ليس بينهما قاسم مشترك |
وعليه يكون القاسم المشترك الأكبر للعددن = حاصل ضرب الأعداد الموجودة في العمود الأخير من الجدول =12
و المضاعف المشترك الأصغر = حاصل ضرب الأعداد الموجودة في العمود الأخير × الأعداد الموجودة في الصف الأخيرمن الجدول =504
وفي رأي الشخصي أن أسهل طريق لحساب المضعف المشترك الأصغر لعددين هي قسمة حاصل ضرب العددين على القاسم المشترك الأكبر لهما
فالمثال الأخير العددان 72,84 قاسمهما المشترك الأكبر 12 وحاصل ضربهما هو 72×84
|
وعليه يكون المضاعف المشترك الأصغر=72×84 قسمة 12أي 504 وهو الناتج نفسه بالطريقة الأخرى |
تطبيق متقدم : عددان قاسمهما المشترك الأكبر 12 , ومضاعفهما المشترك الأصغر 504 وأحدهما84 فما هو العدد الآخر ؟
من السؤال يتضح أن 504= المضاعف المشترك الأصغر
القاسم المشترك الأكبر= 12
حاصل ضرب العددين = القاسم ×المضاعف
504×12=س×84
وعليه يكون العدد الآخر س= 504×12قسمة 84= 72
المضاعف المشترك الأصغر×القاسم المشترك الأكبر= حاصل ضرب العددين
تمارين : احسب القاسم المشترك الأكبر و المضاعف المشترك الأصعر للعددين 144 , 210 بطريقتين مختلفتين
الحل : التحليل الشجري:
| العدد الأول= 144 | العدد الثاني =210 |
|
|
|
|
|
|
|
العوامل الأولية هي : 2 أربع مرت و 3 مرتين |
العوامل الأولية هي: 2 و 3 و5 و 7 |
| المضاعف المشترك الأصغر هو حاصل ضرب الأعداد الأولية المشتركة وغير المشتركة التي تظهر أكثر المرات عدداً | |
|
المضاعف المشترك الأصغر= 2 × 2 ×2 ×2 × 3× 3×5 ×7 = 5040 |
|
| القاسم المشترك الأكبر هو حاصل ضرب الأعداد الأولية المشتركة التي تظهر أقل المرات عدداً | |
|
القاسم المشترك الأكبر= 2 × 3=6 |
|
الحل بالطريقة السريعة التي لا تعتمد على القواسم الأولية
| العدد الأول | العدد الثاني | يقبلان القسمة على |
| 144 | 210 | 2 |
| 72 | 105 | 3 |
| 24 | 35 |
ليس بينهما قاسم مشترك |
| القاسم المشترك الأكبر | 2 × 3=6 | |
| المضاعف المشترك الأصغر | 6×24×35=5040 | |
ملاحظــة :
ويمكن إيجاد ( مضاعفات مشتركة لثلاثة أعداد أو أكثر بتوسيع المطالب السابقة والمثال التالي لإيجاد المضاعفات لثلاثة أعداد هي 35 ,30 ، 28
يمكننا استخدام التحليل الشجري
| العدد الأول= 72 | العدد الثاني =84 | العدد الثاني =28 |
|
|
|
|
|
|
|
|
|
العوامل الأولية هي : 2ثلاث مرات و 3مرتين |
العوامل الأولية هي : 2 مرتين و3و 7 |
العوامل الأولية هي: 2 مرتين و 7 |
|
المضاعف المشترك الأصغر هو حاصل ضرب الأعداد الأولية المشتركة وغير المشتركة التي تظهر أكثر المرات عدداً |
||
|
المضاعف المشترك الأصغر= 2 × 2 ×2×3× 3 ×7 = 504 |
||
|
القاسم المشترك الأكبر هو حاصل ضرب الأعداد الأولية المشتركة التي تظهر أقل المرات عدداً |
||
|
القاسم المشترك الأكبر= 2 × 2 |
||
144 , 210
م.م.أ ( 144 ,210 )
نخز عامل مستر 2 بين العددين
م.م.أ ( 144 ,210 ) = 2 م.م.أ ( 72,105)
105 . 72 يقبلان القسمة على 3
2 م.م.أ ( 72,105)= 2 ضرب 3م.م.أ ( 35, 24)
ونظلرا لأن ( 35, 24) ليس بينهما قاسم مشترك يكون القاسم المشتر لأكبر للعددين 2 ضرب 3 والمضاعف المشترك الأصغر = 2 × 3×35× 24
بالطريقة نفسها يمكن حساب
ملاحظة : فال كون احد العددين أحد مضاعفات العدد الثاني مثل 12 , 36 أو 24, 48 لا حاجة لإجراء العملية فالمضع المشترك يكون هو العدد الأكبر وفي الوقت نفسه
يكون العدد الأصغر هو القاسم المشترك الأكبر