الحجـــــوم

                 ان تدريس مفهوم الحجـوم لابد له من وسيلة توضح بشكل مباشر ذلك وهي  توفير مجموعة من المكعبات المتداخلية ذات الألوان المتعددة حيث يطلب بناء مكعبات وذلك لان أفضل طريقة لذلك أن يقدم الحجم على مراحل

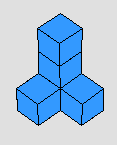
              (1) اللعب باستخدام عدة أشكال تمثل حجـوما 

                   يتم بعرض على التلميذات مجموعة من الأشكال المختلفة والتي تمثل حجوما مختلفة

              (2) مرحلة بناء المفهوم 

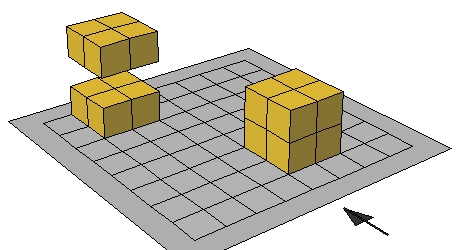
                    يتم عرض على التلميذات مجموعة من الأشكال المبنية باستخدام المكعبات

                    المتداخلة أمامهم ويتم المناقشة حول ذلك 

                 - عن عدد المكعبات التي يحتويها الشكل ، وعن الأشكال التي تظهر أمام التلميذة من الاوجه المختلفة للشكل 

                    وذلك كما في الرسم التالي في الشكل التالي  :

               (3) بقاء الحجم :

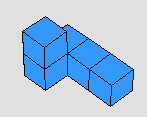
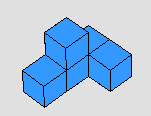
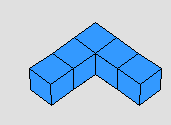
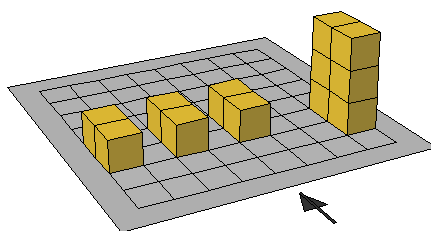
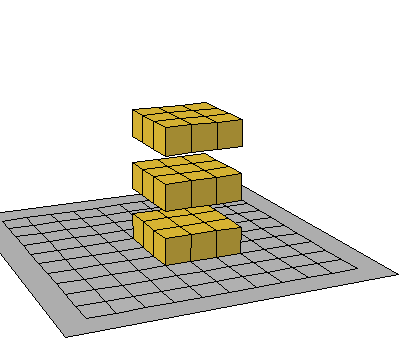
                  - يتم ملاحظة الحجم بواسطة المكعبات المتداخلة  فالأشكال التالية كل منها مكون من خمس مكعبات وعليه يكون حجم كل منها 5 مكعبات رغم اختلاف الأشاكل

 مما يعزز مفهوم بقاء الحجم

                     ويتم ذلك بعرض مجموعة من الأجسام ويطلب حساب حجم كل مجسم و مقارنة الحجوم في تلك الأجسام فيكون تعزيز لمفهوم أكبر من  ومفهوم أصغرمن أو مفهوم التساوي 

              نتيجـة : ويمكن توضيح كذلك انه إذا أنقسم جسم إلى قسمين أو أكثر فان :

              مجموعة حجـوم الأقسام الناتجة = حجم الجسم الأصلي 

              - وذلك موضح بالرسم :

                                               قيــاس الحــجم           

                                         ( الصف السادس الابتدائي )

                 يتم قياس الحجم باستخدام وحدة الحجوم ، ووحدة الحجوم هي مكعب طول ضلعه وحدة أطوال 

                  ولكي نقيس حجم جسم معين نحسب عدد وحدات الحجوم التي يحتويها هذا الجسم 

                  نستخدم لذلك مكعبات متداخلة لتوضيح ذلك أمام التلميذات يعرض عاى النحو بالرسم كما في الصفحة التالية ( مكعب صغير (أ) وهى وحدة حجم لحساب حجم المكعب الكبير (ب) ويتم عرض ذلك أمام التلميذات ويطلب منهم مقارنة حجم الجسمين فنجد بان المكعب (ب) يحتوى على 27 مكعب من (أ)

              أي أن حساب عدد الوحدات التي احتواها المكعب الكبير يتم بتقسيمه على  طبقات فهو يحتوى على ثلاث طبقات أفقيه  وكل طبقة تحتوى على 9 وحدات 

              - فيكون عدد الوحدات = 3× 9 = 27 وحدة

              فهذا يدل على أن حجم المكعب = عدد الطبقات × عدد وحدات كل طبقة اذن يمكن القول بان العدد 27 هو قياس حجم المكعب 

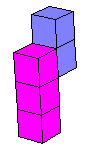
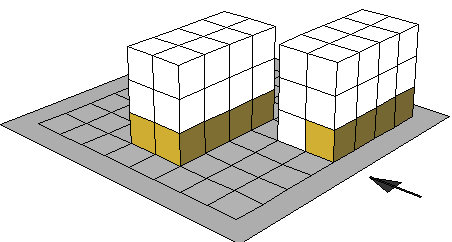
وقد يكون الشكلان مختلفين ولهما الحجم نفسه فالشكل الأول الأيمن عبارة عن عمارة من ثلاثة طوابق في كل طابق شقتين بينما الشكل الاخر عبارة عن عمارة من دور واحد فيه 6 شقق

مما يعزز مفهوم بقاء الحجم

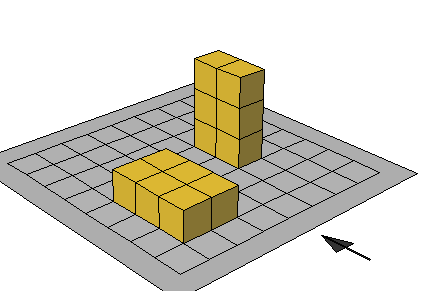
                                       بناء أجسام من المكعبـات

                 إذا كان لدينا مجموعة من المكعبات المتساوية البعد ( المكعبات المتداخلة ) فعند رصف عدد من هذه المكعبات بمحاذاة بعضها ، فاننا نحصل على شكل 0

              فهنا الهدف هو تعريف التلميذات على تجميع المكعبات بأشكال مختلفة فيتم عرض المكعبات على التلاميذ ويطلب منهم إجراء أجسام باستخدام هذه المكعبات 0

                  فيمكن من الرسم التالي يبين لنا انه باستخدام أربع مكعبات فإننا يمكن أن نحصل على أوضاع مختلفة لمكعبات ( أربعة أشكال ) 

              ويطلب من التلاميذ قياس حجم الجسم الناتج  بلا شك فان مقياس الحجم في جميع هذه الحالات هو أربعة مكعبات 

               وإذا استخدمنا (10) مكعبات لبناء جسم ، فان مقياس حجمه يكون مساويا لـ    (10)

المكعبات المتداخلة تزيد قدرة الطالب على التصور والتخيل  فكثير من الطلاب يصعب عليهم عد المكعبات التي يتكون منها الشكل التالي                                                                                                                             

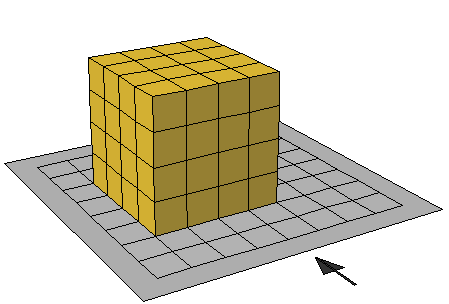
والطريقة المثلى هي  وضع الشكل في طبقات فوق بعضها على النحو التالي

ويمكن تقديم الحجوم على أنها عمارة مكونة من عدد من الأدوار وفي كل دور عدد من الشقق وكل مكعب يمثل شقة فعدد الشقق في العمارة هو المقصود بالحجم

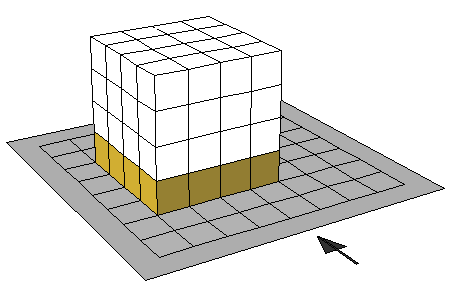
من الشكل السابق يتضح ان العمارة مكونة من اربعة طوابق وفي كل طابق 16 شقة  وعليه يمكن حساب عدد الشقق )الحجم) من خلال حساب عدد الشقق في الطابق الواحد مضروبا في عدد الأدوار

وبالطريقة نفسها يمكن حساب حجم الشل التالي

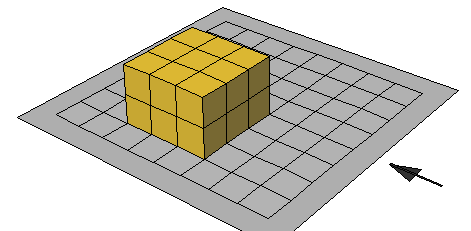
وليس بالضرورة أن يكون الشكل في صورة عمارة تقليدية في شكل مكعب  أو شكل آخر فقد يكون الشكل احد الشكال التالية  ويمكن حساب حجم الشل من خلال عد المكعبات

                  تدريب   : احسب حجم كل مجسم ( عدد المكعبات ) = الحجم  

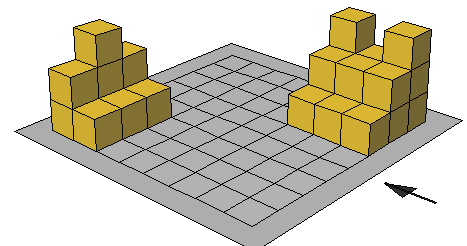
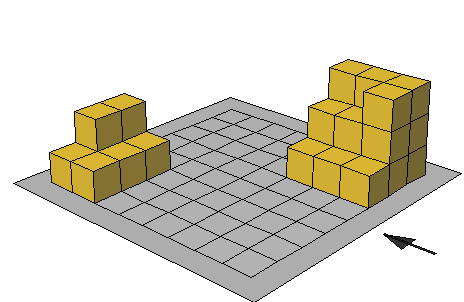
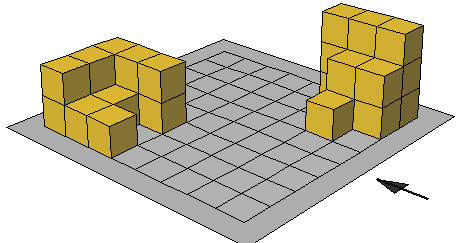
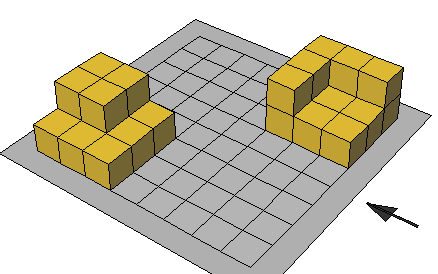
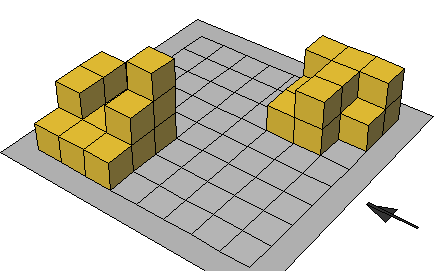
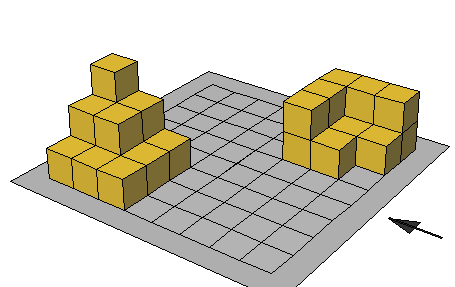
               حجم متوازي المستطيلات 

                    الهدف هو إن تستنتج التلميذة صيغة لحجم متوازي المستطيلات وتطبيقها لتوضيح ذلك فيتم الخطوات التالية :

              1- يزدد التلميذات بالمكعبات المتداخلة أي وحدة المكعب  لقياس الأبعاد 0

              2- يتم عرض صندوق على شكل متــوازي مستطيلات ويسأل ما هو عدد

                  المكعبات التي يحتاجها التلميذة لملىء هذا الصندوق أي ما عدد المكعبات التي تحتاجها التلميذة لرضف الطبقة الأولى من المكعب 0

                   فيكون الخطوة (1)

              -   ما عدد المكعبات لعمل صف واد؟ فيكون 2 مكعب 0  

                   خطوة (2)

              -   ما عدد المكعبات التي تلزمنا لعمل طبقة واحد ؟ فيكون  2× 3 مكعب0

                   خطوة (3)

                  ما عدد المكعبات التي  تلزم لعمل 4 طبقات ؟

              - فيكون عدد المكعبات المستعملة  2× 3 × 4 مكعب 

                 وبالمناقشة وتوضيح ذلك بالرسم كما في الصفحة التالية :

              - تتوصل التلميذات إلى أن الحجم = الطول × العرض × الارتفاع

                 وهنا يتم توضيح للتلميذات أن الحجم للشكل طول ضلعه اسم يسمى سنتمتر مكعب 

                  اذن حجم المكعب   = سم 3

                 وكذلك التدريبات التالية : توضح حجم متوازي المستطيلات 

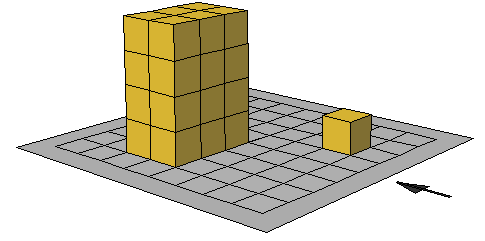
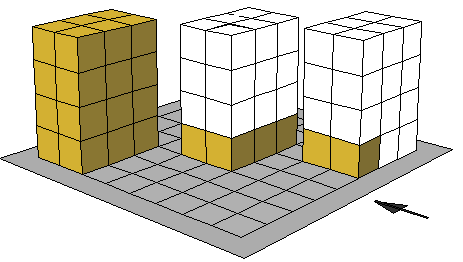
حجــم المكعـب

      يمثل المكعب حالة خاصة من متوازي المستطيلات ، فإذا استوعب التلميذات متوازي المستطيلات فيكون من السهل فهم حجم المكعب 

              فيعطي مجموعة من المكعبات ويطلب من التلميذات بناء مكعب طول حرفه 3 مكعبات

                   فهنا يتم سؤالهم بالخطوة الأولى كم مكعب نحتاج لرصف الطبقة الأولى  والطبقة الثانية وهكذا

              فهنا يدرك التلميذات بأنهم يحتاجون إلى 27 مكعب 

              وذلك ناتج من القانون 0

              عدد المكعبات المستخدمة  = 3 × 3 × 3  = 27 مكعب

              - حجم المكعب =   27 سم3

                اسـتنتاج:

                حجم المكعب = بعد المكعب × نفسه × نفسه 0

                         [حجم المكعب = (بعد المكعب)3 ]

                 وتوضيح ذلك بالرسم التالي:

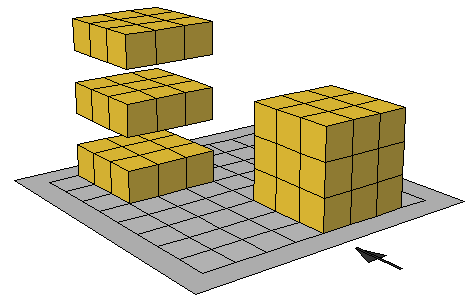
والمكعب المكون من 4 مكعبات في الطالق الواحد معدد الطوابق 2 يكون الحجم=8 مكعبات