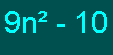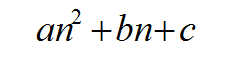
أ) تطبيقات باستخدام برمجية الحد النوني من الدرجة الثانية لعاملين:
ويمكن الوصول إلى هذه البرمجية بالرجوع إلى موقع التعليم الإلكتروني لتطوير تدريس الرياضيات للدكتور عباس غندورة (www.aghandoura.com) ، وذلك في القسم الخاص بتعليم الرياضيات للموهوبين كما في الشكل التالي:
تستخدم هذه البرمجية لإيجاد الحد النوني للمتتابعات ذات الفرق الثاني ، حيث تعرض البرمجية متتابعةً موضحةً فيها ثبات الفروق عند الفرق الثاني ،
وتطلب من المستخدم تجريب قيم تحدد مضاعفات للمتغير n ، بالإضافة إلى قيم للحد الثابت حتى الوصول إلى الحد النوني المطلوب.
علماً بأن الحد النوني للمتتابعة ذات
الفرق الثاني
معادلة الدرجة الثانية
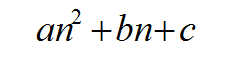
ملاحظة/ هذا النوع من
المتتابعات الذي تحاكيه البرمجية يعتمد على عاملين فقط هما : معامل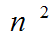 
و الحد الثابت.
متتابعة (1):
المتتابعة التالية : 4 ، 7 ، 12 ، 19، 28 .....
تم وضعها في البرمجية وتوضيح ثبات الفروق في الحد الثاني كما في الشكل:
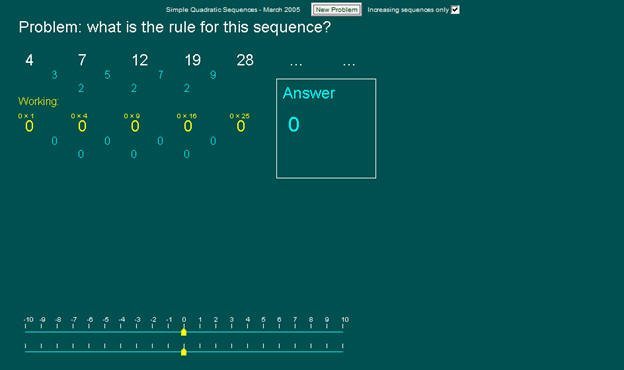
نلاحظ في المتتابعة الجديدة أيضاً أن الفروق ثبتت عند الفرق الثاني لذا فالحد النوني للمتتابعة هومعادلة الدرجة الثانية
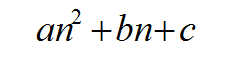
وللحصول على قيم a ، b ، c مباشرةً للتعويض بها في البرمجية والحصول على الحد النوني نستخدم صيغ الفرق الثابت ، وحدود متتابعة الفروق :
قيمة الفرق الثابت في المسألة المعطاة في البرمجية هي 2
2a=2
a=1
قيمة الحد الأول في الفرق الأول 3
3a+b= 3
3 (1) + b =3
b= 0
والآن نعوض بقيمة الحد الأول من المتتابعة
a+b+c = 4
1 + 0 + c = 4
c = 4 - 1
c = 3
وبتعويض قيم a,b,c في خطوط الأعداد أسفل البرمجية ، ولأن هذه البرمجية خاصة لعاملين فستطلب فقط قيمة معامل ن تربيع (a) والحد الثابت (c).
نعوض بقيمتهما في خطي الأعداد أسفل البرمجية فنصل إلى الحل.
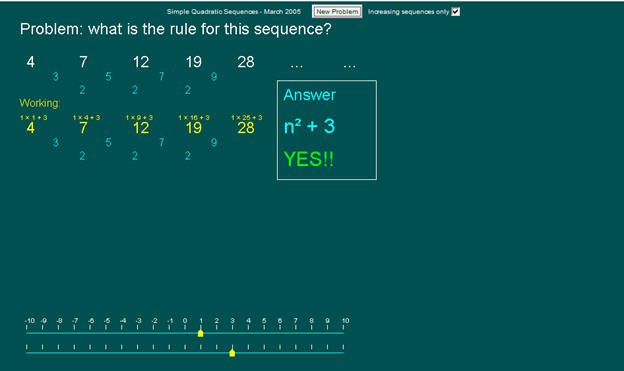
إذن الحد النوني للمتتابعة المعطاة
هو :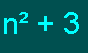
*
لنجرب مسألةً أخرى بالضغط على المستطيل 
أعلى
البرمجية:
متتابعة (2):
- لدينا المتتابعة التالية: 3، 30، 75، 138، 219....
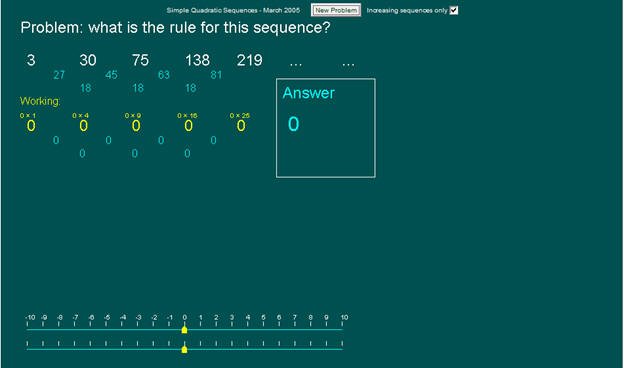
نلاحظ في المتتابعة الجديدة أيضاً أن الفروق ثبتت عند الفرق الثاني لذا فالحد النوني للمتتابعة هومعادلة الدرجة الثانية
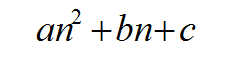
وللحصول على قيم a ، b ، c مباشرةً للتعويض بها في البرمجية والحصول على الحد النوني نستخدم صيغ الفرق الثابت ، وحدود متتابعة الفروق :
قيمة الفرق الثابت في المسألة المعطاة في البرمجية هي 18
2a=18
a=9
قيمة الحد الأول في الفرق الأول 27
3a+b= 27
3 (9) + b =27
b= 0
والآن نعوض بقيمة الحد الأول من المتتابعة
a+b+c = 3
9 + 0 + c = 3
c = 3 - 9
c = -6
وبتعويض قيم a,b,c في خطوط الأعداد أسفل البرمجية ، ولأن هذه البرمجية خاصة لعاملين فستطلب فقط قيمة معامل ن تربيع (a) والحد الثابت (c).
نعوض بقيمتهما في خطي الأعداد أسفل البرمجية فنصل إلى الحل.
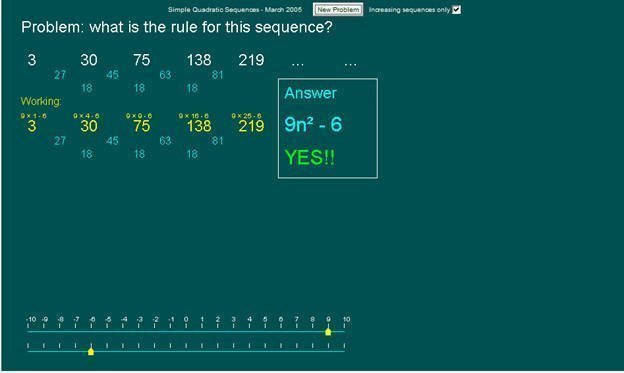
إذن الحد النوني للمتتابعة المعطاة
هو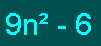
متتابعة (3):
المتتابعة التالية : 6 ، 15 ، 30 ، 51، 78 .....
تم وضعها في البرمجية وتوضيح ثبات الفروق في الحد الثاني كما في الشكل:
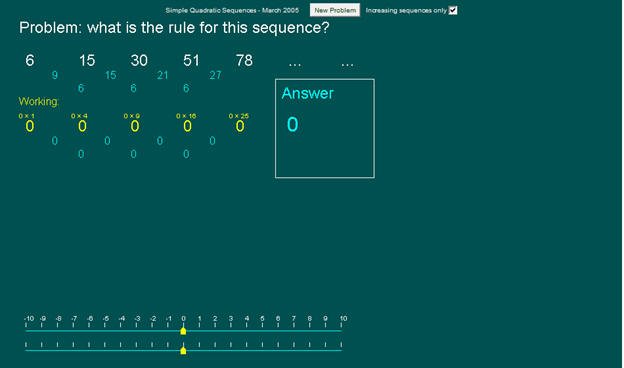
نلاحظ في المتتابعة الجديدة أيضاً أن
الفروق ثبتت عند الفرق الثاني لذا فالحد النوني للمتتابعة هومعادلة
الدرجة الثانية
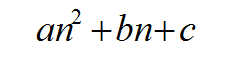
وللحصول على قيم a ، b ، c مباشرةً للتعويض بها في البرمجية والحصول على الحد النوني نستخدم صيغ الفرق الثابت ، وحدود متتابعة الفروق :
قيمة الفرق الثابت في المسألة المعطاة في البرمجية هي 6
2a=6
a=3
قيمة الحد الأول في الفرق الأول 9
3a+b= 9
3 (3) + b =9
9 + b = 9
b= 0
والآن نعوض بقيمة الحد الأول من المتتابعة
a+b+c = 6
3 + 0 + c = 3
c = 3 -3
c = 0
وبتعويض قيم a,b,c في خطوط الأعداد أسفل البرمجية ، ولأن هذه البرمجية خاصة لعاملين فستطلب فقط قيمة معامل ن تربيع (a) والحد الثابت (c).
نعوض بقيمتهما في خطي الأعداد أسفل البرمجية فنصل إلى الحل.
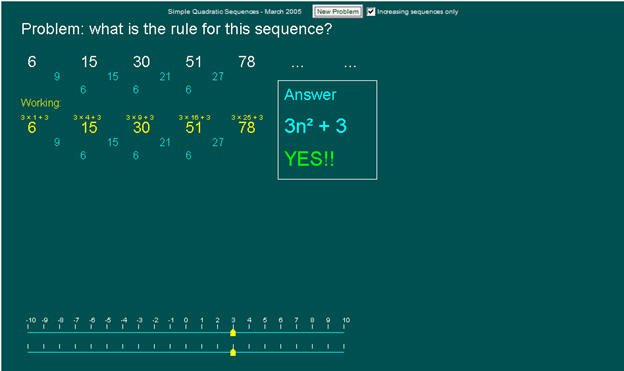
إذن الحد النوني للمتتابعة المعطاة
هو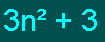
متتابعة (4):
المتتابعة التالية : 2 ، 8 ، 18 ، 32، 50 .....
تم وضعها في البرمجية وتوضيح ثبات الفروق في الحد الثاني كما في الشكل:
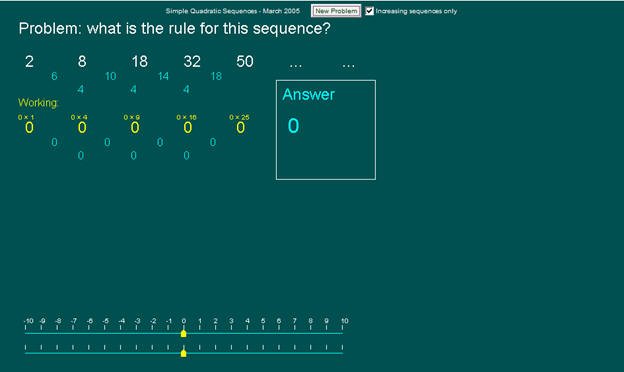
نلاحظ في المتتابعة الجديدة أيضاً أن
الفروق ثبتت عند الفرق الثاني لذا فالحد النوني للمتتابعة هومعادلة
الدرجة الثانية
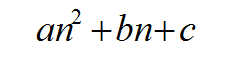
وللحصول على قيم a ، b ، c مباشرةً للتعويض بها في البرمجية والحصول على الحد النوني نستخدم صيغ الفرق الثابت ، وحدود متتابعة الفروق :
قيمة الفرق الثابت في المسألة المعطاة في البرمجية هي 4
2a=4
a=2
قيمة الحد الأول في الفرق الأول 6
3a+b= 6
3 (2) + b =6
6 + b = 6
b= 0
والآن نعوض بقيمة الحد الأول من المتتابعة
a+b+c =2
2 + 0 + c = 2
c = 2-2
c = 0
وبتعويض قيم a,b,c في خطوط الأعداد أسفل البرمجية ، ولأن هذه البرمجية خاصة لعاملين فستطلب فقط قيمة معامل ن تربيع (a) والحد الثابت (c).
نعوض بقيمتهما في خطي الأعداد أسفل البرمجية فنصل إلى الحل.
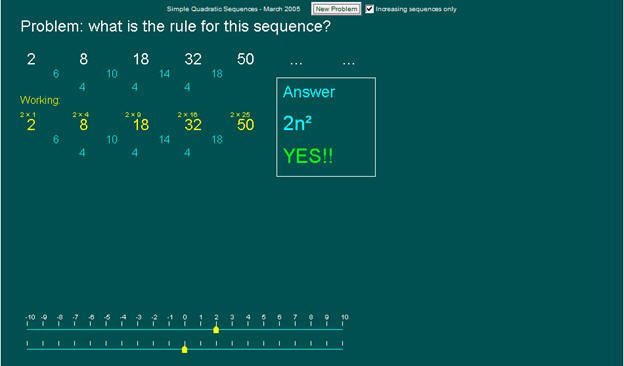
إذن الحد النوني للمتتابعة المعطاة
هو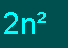
متتابعة (5):
المتتابعة التالية : -1 ، 26 ، 71 ، 134، 215 .....
تم وضعها في البرمجية وتوضيح ثبات الفروق في الحد الثاني كما في الشكل:
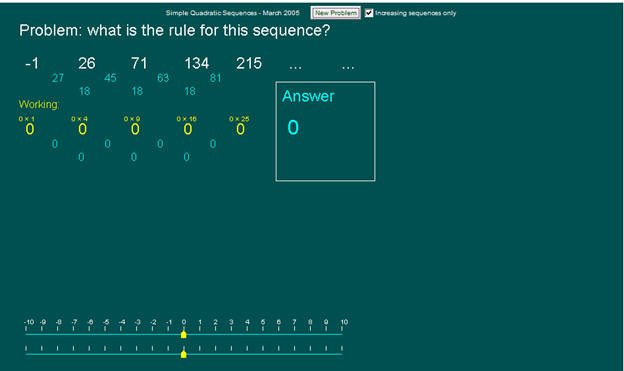
نلاحظ في المتتابعة الجديدة أيضاً أن
الفروق ثبتت عند الفرق الثاني لذا فالحد النوني للمتتابعة هومعادلة
الدرجة الثانية
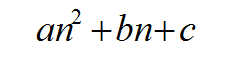
وللحصول على قيم a ، b ، c مباشرةً للتعويض بها في البرمجية والحصول على الحد النوني نستخدم صيغ الفرق الثابت ، وحدود متتابعة الفروق :
قيمة الفرق الثابت في المسألة المعطاة في البرمجية هي 18
2a=18
a=9
قيمة الحد الأول في الفرق الأول 27
3a+b=27
3 (9) + b =27
27 + b = 27
b= 0
والآن نعوض بقيمة الحد الأول من المتتابعة
a+b+c =-1
9 + 0 + c = -1
c = -1-9
c = -10
وبتعويض قيم a,b,c في خطوط الأعداد أسفل البرمجية ، ولأن هذه البرمجية خاصة لعاملين فستطلب فقط قيمة معامل ن تربيع (a) والحد الثابت (c).
نعوض بقيمتهما في خطي الأعداد أسفل البرمجية فنصل إلى الحل.
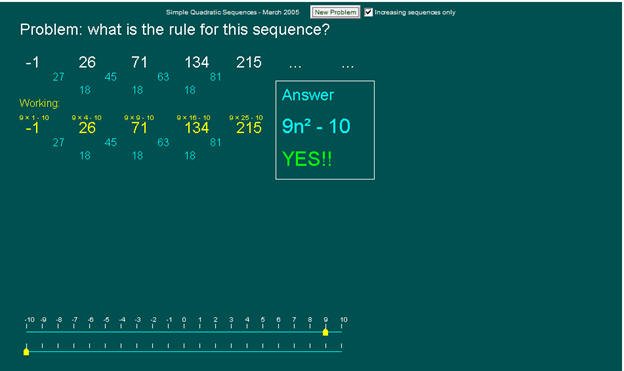
إذن الحد النوني للمتتابعة المعطاة
هو