عند
أضافت كمية ألي كمية أخرى من أعداد أو أشياء على أن تكون من نفس النوع نكون قد
أجرينا عليها عملية جمع .
عمليات الحساب الأساسية :
( الجمع – الطرح – الضرب – القسمة )
عمليتي الجمع والضرب والعمليتين العكسيتين لهما الطرح والقسمة تسمى هذه بالعمليات الأساسية لأنها أساس دراسة الرياضيات في المرحلة الابتدائية والمراحل اللاحقة لها.
فعند تقديم عملية الجمع على أنها اتحاد مجموعات منفصلة يتعرف التلميذ من خلالها على عملية الجمع وبنفس الطريقة يمكن أن يعرف عن طريق الفرق بين المجموعات المنفصلة على عملية الطرح فمن المعروف أن الطرح هو عملية عكسية لعملية الجمع.
ومن الوسائل التي تساعد على تقديم هذه المفاهيم هي مكعبات دينز أو ( مكعبات الأساس عشرة ) .
عند
أضافت كمية ألي كمية أخرى من أعداد أو أشياء على أن تكون من نفس النوع نكون قد
أجرينا عليها عملية جمع .
مثال (1)
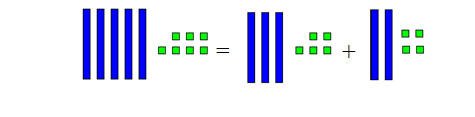
لجمع 9+5 يتم تجزئة العدد 5 إلى العدديين 1 و 4 لأن 9 +1 =10
( مكونات العشرة ) ثم يضاف العدد الآخر هو 4 إلى 10 ليكون الناتج 10 + 4 = 14 .
أي أن :
9 + 5 = 9 + ( 1 + 4 ) = ( 9 + 1 ) + 4 = 10 + 4 +14
والشكل التالي يوضح ذلك :
مثال
(2)
بنفس الطريقة يمكن جمع 7 + 4
يكون
نشاط
اجمع الأعداد التالية ؟
8 + 5 =......
6 + 7 =.......
الجمع بدون حمل :
الطريقة الأولى :-
باستخدام مكعبات دينز يمكن تعلم عمليات الجمع التي لا تحتاج إلى حمل .
مثال
(1)
22 +35
اولاً نمثل العدديين السابقين :
ثانيا ًنجمع الوحايد مع بعض :
مع تصبح
ونجمع الأصابع مع بعض :
مع تصبح
بالتالي
نشاط
باستخدام مكعبات دينز اجمعي الأعداد التالية ؟ .
أ) 43 + 55 = .....
ب) 82 + 16 = .......
الطريقة الثانية :-
باستخدام مكعبات دينز يمكن كذلك تعلم عمليات الجمع التي لا تحتاج إلى حمل بطريقة ثانية كالتالي :
مثال (1)
24 +35 =
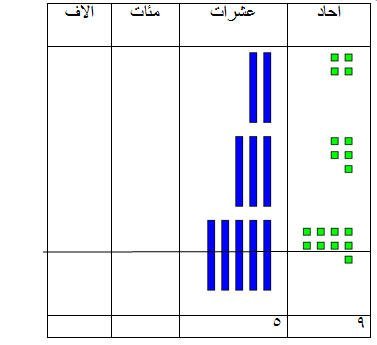
بالتالي
24 + 35 = 59
مثال (2)
30 + 32 =
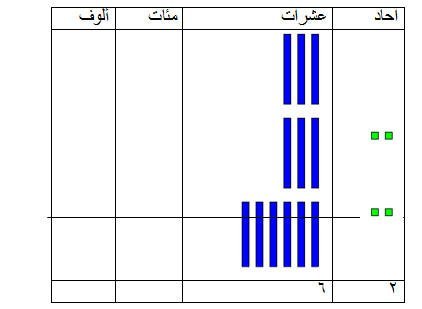
بالتالي:
30 + 32 = 62
مثال (3)
20 + 20 =
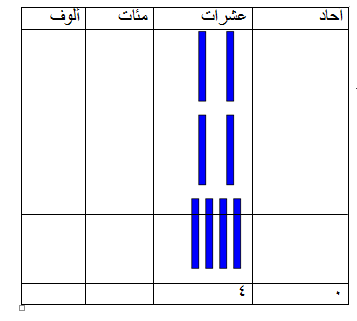
بالتالي:
20 + 20= 40
نشاط
باستخدام البطاقة أجرى عمليات الجمع التالية:
( أ )
11 + 88=
( ب )
55+ 14=
( ج )
23+73=
الجمع بالحمل :
المقايضة :
بإمكان الطلاب أن يتدربوا على المقايضة ، إذ يمكن مقايضة عشر وحدات بإصبع واحد
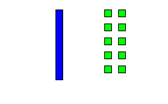
ومقايضة عشر مربعات بمربع واحد
ومقايضة عشرة مربعات بمكعب واحد
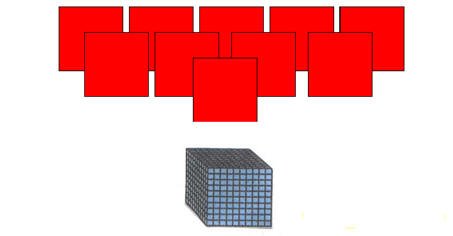
وعندما ترسخ فكرة المقايضة يمكن تقديم الجمع باستخدام مفهوم الحمل .
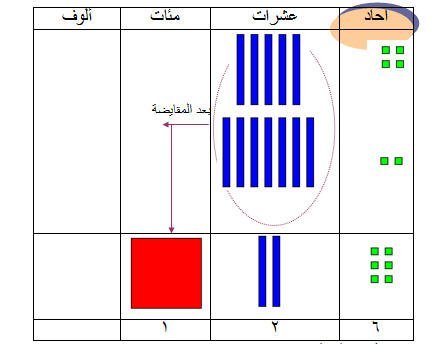
مثال (1)
لإيجاد 54+72 تقوم التلميذة بالإجابة على الأسئلة التالية:
1- كم عدد الوحدات؟ (6) هل بالإمكان المقايضة ؟ ( لا )
2- كم العدد الإجمالي للأصابع ؟ (12) هل بالإمكان المقايضة ؟ ( نعم )
3- كم عدد الأصابع المتبقية بعد علميتي المقايضة (2)
بالتالي :- 54 + 72 = 126