الحدود الجبرية

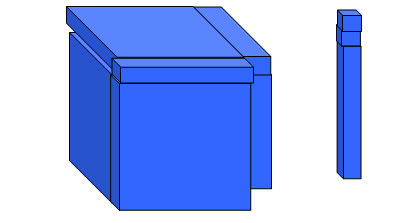
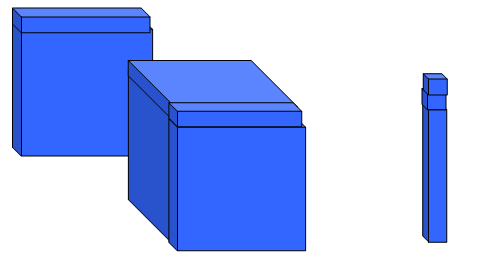
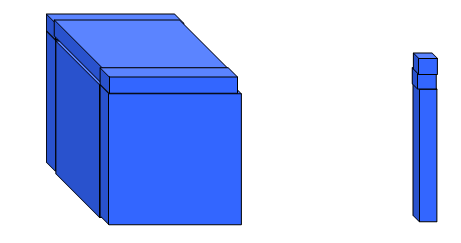
هناك العديد من المحاولات الجادة التي تهدف إلي تبسيط المفاهيم الرياضية إلى واقع محسوس ومن تلك المحاولات مكعبات الأساس عشرة حيث يمكن اعتبار المربع  10 ×10 × 10 س³

والمستطيل الذي يمثل 10 × 10 س²

والمستطيل 10 × 1 بمثابة س

والمربع الصغير الذي يمثل الوحدة مما يمكننا من تمثيل العديد من المقادير الجبرية وضربها .

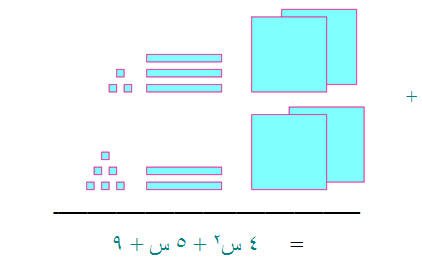
مثال (1 )

يمكن جمع (2 س² + 3س + 3)  و( 2س² + 2س + 6 )

بالتالي :-

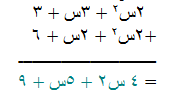
مثال (2)

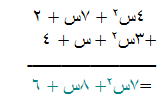
مثال (3)

يمكن تمثيل عملية طرح( س2 + س +)2 من (2س + 3س + 4 )

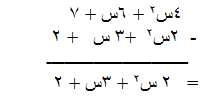
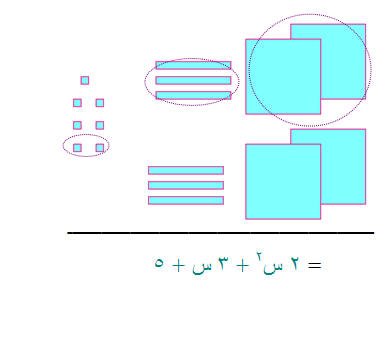
مثال ( 4 )

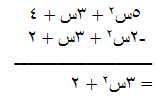
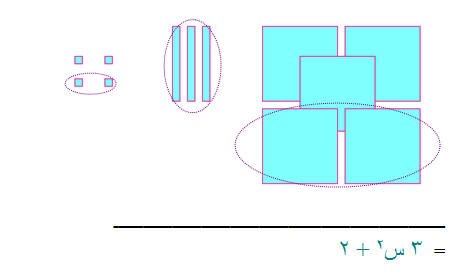
مثال ( 5  )

يمكن تمثيل عملية ضرب  ( 3س + 2 ) × ( 2س + 1 )  كالتالي :-

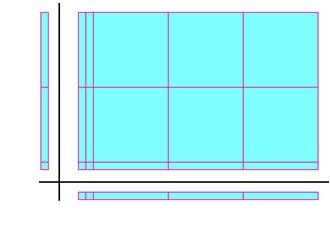
( 3س + 2 ) ( 2س + 1 ) = 6س² + 3س + 4س + 2

                                    = 6س² + 7س + 2

مثال ( 6 )

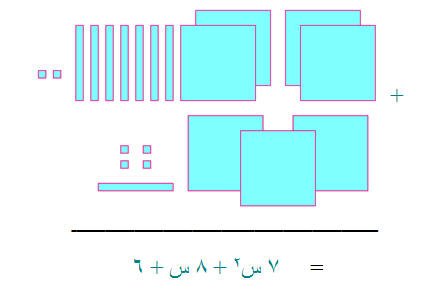
يمكن تمثيل ( 2س + 1 ) ( س + 3 ) على النحو التالي :-

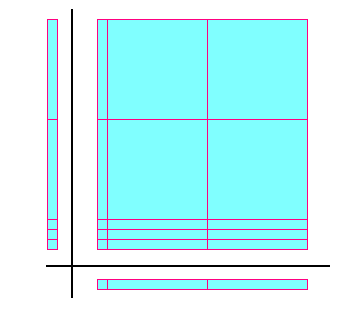
 ( 2س + 1 ) (2 س + 3 ) = 4س² + 6س +2 س + 3

                                    = 4س² + 8 س + 3

مثال ( 7 )

يمكن تمثيل ( س + 4 ) ( س+ 1 ) , ( س + 2 ) ( س + 3 ) , وكذلك ( س + 2 ) ( س + 2 ).

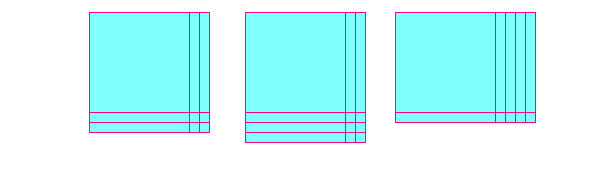
مثال ( 8 )

يمكن تمثيل ( س + 1 )³ بمكعبات دينز على النحو التالي :-

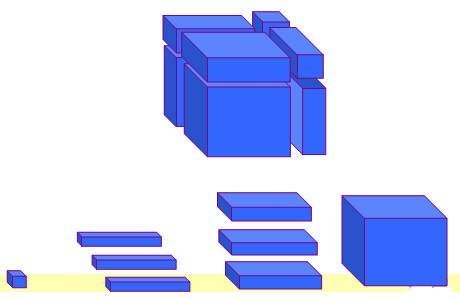
( س + 1 ) ³ = س3 + 3 س2 + 3س + 1

على اعتبار أن:

 يمكن تمثيل عملية ضرب ( س + 2ص ) ( س + ص )

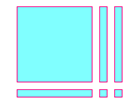
( س + 2ص ) ( س + ص ) =

                               = س² + س ص + 2س ص + 2ص²

                               = س² + 3س ص + 2ص²

كما يمكن تمثيل المتطابقات الأساسية كالتالي :

مربع مجموع حديين

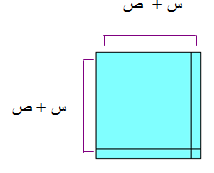
( س + ص )² = س² + 2س ص + ص²

مربع الفرق بين حديين

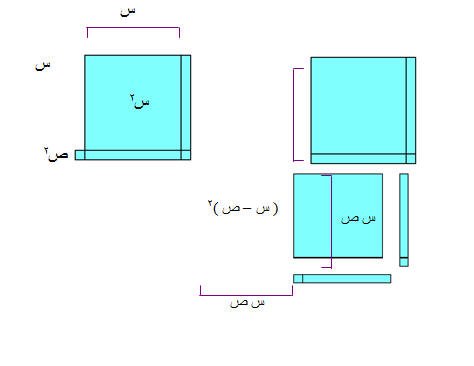
 ( س- ص )² = س² + 2س ص+ ص²

الفرق بين مربعين

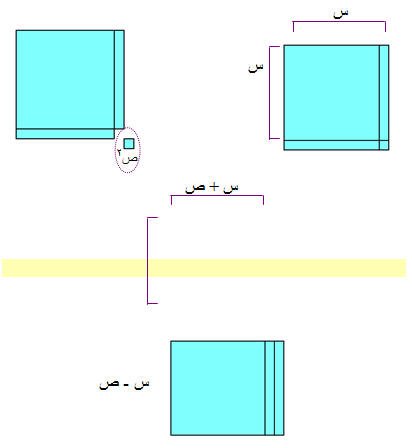
( س² – ص² ) = ( س + ص ) ( س – ص )            

وعلى اعتبار أن:-

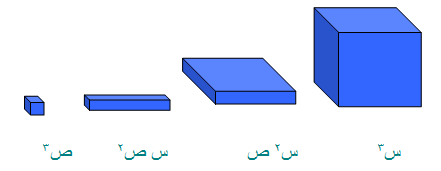
مكعب مجموع حديين

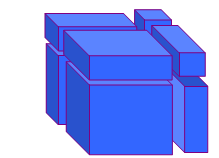
(س+ ص ) ³ = س³ + 3س² ص + 3 س ص² + ص³

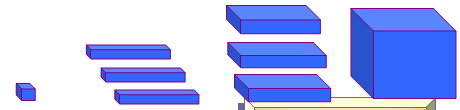
الفرق بين مكعبين

يمكن تمثيل متطابقة الفرق بين مكعبين بطريقة مشابهة لمكعب مجموع حدين حيث يمثل س طول ضلع المكعب الكبير المكون من القطع مجتمعة وبالتالي يكون حجم المكعب الكبير س³ .

ويكون حجم المكعب الصغير هو ص3 وعند الطرح   (استبعاد ) المكعب الصغير الذي حجمه ص3 من حجم الشكل المتكونة من القطع مجتمعة الذي حجمه س3 ويكون الشكل التالي يمثل المتطابقة  س3 – ص3 .

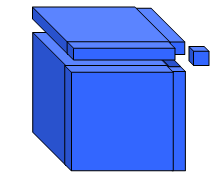
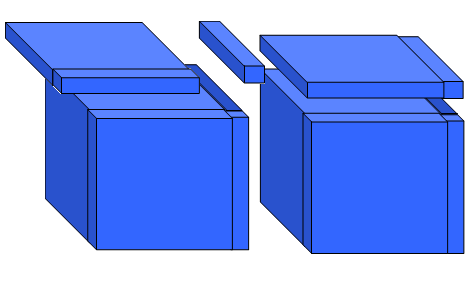
وهذا الحجم عبارة مجموع حجوم القطع المكونة له وهذه القطعة حجومها كالتالي :

القطعة السفلية حجمها = س×س×(س- ص )

ومتوازي المستطيلات الكبير حجمه = س× ص× (س- ص )

ومتوازي المستطيلات الصغير حجمه = ص×ص× (س- ص)

وهذا معناه :

س³ – ص³ = س² ( س- ص ) + س ص  ( س- ص ) + ص² ( س- ص ) .

               = ( س - ص ) (س² + س ص +  ص² )

مجموع مكعبين 

لإيجاد مفكوك مجموع مكعبين نتبع الخطوات التالية :-

§         بناء مكعب واعتباره  س3 .

§         يضاف المكعب الصغير  ص³ على المكعب  س³ فنحصل على الشكل  س3 + ص3

§         نقتطع الشكل الذي حجمه  ص² ( س + ص )

§         فك الجزء المتبقي وأضافته إلى أحد الجزئيين فيصبح حجمه س ( س – ص ) ( س + ص )

§         وبتجميع الشكل ينتج :

§         س³ + ص³ = ص² ( س + ص ) + س ( س – ص ) (س + ص )

= س ص² + ص³ + س ( س² – ص² )

= س ص² + ص³+ س³ –  س ص²

= ( س + ص ) ( ص² + س² _ س ص )             

 = ( س+ ص )  ( س² – س ص + ص² )

مجموع مكعبين =

 ( مجموع الحديين ) × ( مربع الحد الأول ) – حاصل  ضرب الحديين  + مربع الحد الثاني  .