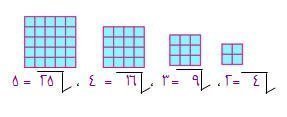
الجذر التربيعي

لإيجاد الجذر التربيعي لعدد ما باستخدام مكعبات دينز نقوم ببناء مربع من ذلك العدد ويكون طول ضلع ذلك المربع مساوياً للجذر التربيعي لذلك العدد .

مثال (1)

يمكن أيجاد الجذر التربيعي للأعداد 4 , 9 , 16 , 25 ببناء مربعات من هذه الأعداد .

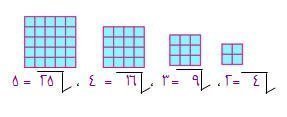
مثال (2)

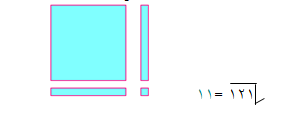
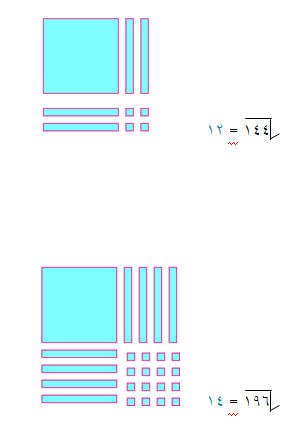
بنفس الطريقة يمكن بناء مربع لإيجاد الجذر التربيعي للعدد 121 , 144 , 196 , 256 على النحو التالي :-

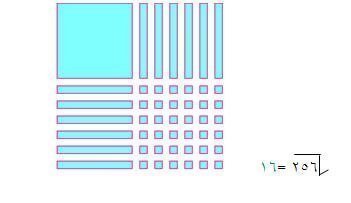
مثال (3)

يمكن  إيجاد الجذر التربيعي للعد 20 على النحو التالي :-

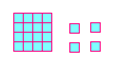
1.  ننشئ اكبر مربع يمكن بناؤه باستخدام الوحدات العشرين . وفي هذه الحالة يكون طول ضلعه 4 وحدات .

2.  نحسب عدد الوحدات المتبقية بعد إتمام الخطوة الأولى          ( 20 – 16 = 4 ) .

3.  نحسب عدد الوحدات اللازمة لإنشاء المربع الذي يزيد طول ضلعه وحدة واحدة عن طول ضلع المربع الذي أنشئ في الخطوة الأولى . وفي هذه الحالة يكون عدد الوحدات اللازمة هو 25 – 16 = 9 .

4.  نقسم الناتج في الحظوة الثانية على الناتج من الخطوة الثالثة. وفي هذه الحالة يكون الناتج 4 تقسيم 9 .

5.  الجذر التربيعي المطلوب يساوي تقريباً طول ضلع المربع في الخطوة الأولى , أي 4 مضافاً ناتج الخطوة الرابعة , ومن ثم فالناتج النهائي يساوي أربعة و أربعة أتساع .  

مثال (4 )

بنفس الطريقة يمكن إيجاد الجذر التربيعي للعدد 56 على النحو التالي :-

1) نبني مربعاً طول ضلعه 7 وحدات , ومن ثم تكون       مساحة  = 49 وحدة  .

2) المتبقي = 56 – 49 = 7 وحدات .

3) مساحة المربع التالي له من المساحة تساوي 8 × 8 = 64 وحدة مربعة

4) الفرق بين الناتجين في كل من الخطوتين الثالثة والأولى يساوي 64 – 49 = 15 وحدة

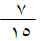5) الجذر التربيعي المطلوب هو       7

مثال ( 5 )

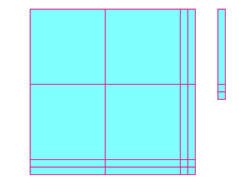
الجذر التربيعي للعدد 496  :-

1.   نبني مربعاً طول ضلعه 22 وحدة , ومن ثم تكون مساحته 484 وحدة مربعة .

2.   المتبقي يساوي 496 – 484 = 12 وحدة .

3.   مساحة المربع التالي له في المساحة= 23 × 23 = 529 وحدة مربعة .

4.  الفرق بين الناتجين في كل من الخطوتين الثالثة والأولى = 529 – 484 = 45 وحده .

5.  الجذر التربيعي المطلوب هو   12  22 .

                                          45

نشاط

أوجدي الجذر التربيعي للأعداد التالية :-

           36  ,  49  , 64   .