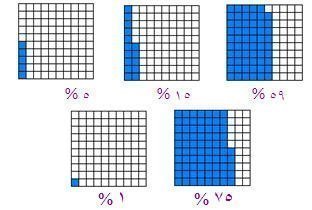
النسبة المئوية
يمكننا استخدام المربع 10×10 في حل العديد من المسائل على النسبة المئوية ولكن يفضل قبل حل المسائل أن تتعامل التلميذات مع صورة للمربع وتظليل جزء منها أو إعطائهن جزء مظلل ويطلب منهن تحديد نسبة الجزء المظلل .

وبعد أن كونت التلميذات فكره عن المربع يمكنهن تصور أن 100% عبارة عن المربع الكبير وان 1% يمكن تمثيله على انه لمربع الصغير. وعليه يمكن تمثيل اقل من 1% أو اكثر من 100% على النحو التالي :
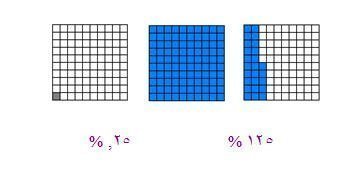
وبالتالي إذا كان المربع الكبير يمثل عددا معينا فان المربع الصغير يمثل هذا العدد مقسوما على 100 , ولإيضاح الفكرة للتلميذات وتقريبها لهن يمكن التفكير في العدد على انه مبلغ يراد تقسيمه على عدد المربعات الصغيرة لمعرفة ما يخص كل مربع .
أي أن حل المسائل المتعلقة بالنسبة المئوية يعتمد اعتمادا كبيرا على فهم طريقة إيجاد قيمة المربع الصغير من الشبكة .

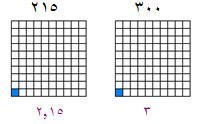
فعلى سبيل المثال إذا كان كامل المربع يمثل (300) شخص فان المربع الصغير يمثل ثلاثة أشخاص أي :
 = 3
= 3
وبنفس الطريقة إذا كان المربع الكبير يمثل 215ريال فان المربع الصغير يمثل 2.15ريالا .
مثال (1)
إذا كان المربع الكبير يمثل (400) شخص . فأوجدي الأتي :
ا)عدد الأشخاص الذين يمثلهم ربع المربع الصغير .
ب)عدد الأشخاص الذين يمثلهم نصف المربع الصغير .
ج)عدد الأشخاص الذين تمثلهم عشرة مربعات صغيره .
د)الجزء الذي يمثل عدد (200) شخص .
هـ)الجزء الذي يمثل عدد (100) شخص .
و) الجز الذي يمثل عدد (40) شخصاً
ز) الجز الذي يمثل عدد (4) أشخاص
· مجموع الأشخاص (400)
· المربع الواحد يمثل (4) أشخاص
· الشخص الواحد يمثل 0.25 % من المربع الكبير
· وبالتالي فان :
· عدد الأشخاص الذين يمثلهم ربع المربع الكبير شخص واحد
· الشخصان يمثلان 0.5 % من المربع الكبير
وبالتالي فان :
· عدد الأشخاص الذين يمثلهم نصف المربع الكبير شخصان
· (10) مربعات تمثل (40) شخصاً
· (200) شخص يمثلون (50 %) من المربع الكبير
· (100) شخص يمثلون (25 % ) من المربع الكبير
· ( 40) شخص يمثلون ( 10 % ) من المربع الكبير
· (4) أشخاص يمثلون ( 1% ) من المربع الكبير
وبعدها يمكن الانتقال إلى الخطوة التي يتم فيها تحديد قيمة معينه لواحد من المربعات الصغيرة أو اكثر من مربع واحد وإيجاد قيمة كامل المربع الكبير .
مثال (2)
إذا كان (12) مربعا صغيرا تمثل العدد ( 30 ) فما العدد الذي يمثله المربع الكبير ؟
لمعرفة المطلوب يجب أن نعرف ما يمثله المربع الواحد الصغير إذا كان ( 12) مربعاً صغيراً تمثل العدد(30) فان المربع الصغير يمثل بـ :
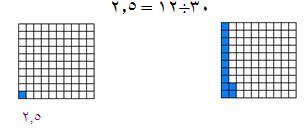
وبالتالي فان المربع الكبير يمثل
2.5 × 100= 250
ويمكن أن يعطي مثل هذا المثال للتلميذات بالصورة التالي :
قص تاجر أقمشة قطعة قماش طولها (30) مترا من أحد الأثواب وكان طول الجزء المقصوص يمثل (12 % ) من طول الثوب .
المطلوب : احسبي طول الثوب ؟
الحل :
1: نفرض أن طول الثوب بالمجهول س
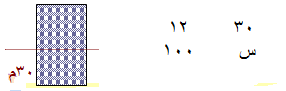
: نضع التناسب التالي : ـــــــ = ـــــــــ
3: حاصل ضرب الطرفين = حاصل ضرب الوسطين
س× 12 = 30× 100 = 300
س= 3000÷ 12
س= 250
ومن هنا نلاحظ أهمية قطع دينز في شرح النسبة المئوية .
مثال (3)
إذا كان 40 مربعاً صغيراً يمثل العدد (860) فان المربع الصغير الواحد يمثل 860 ÷ 40= 21.5 وعليه فان المربع الكبير يمثل 21.5× 100 =0 215
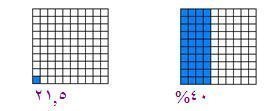
ومثل هذا المثال يعطى للتلميذات بالصورة التالية :
يدفع رب ألا سرة 860 ريالاً إيجارا شهريا للسكن , فإذا كانت نفقات السكن تمثل 40% من دخله فاحسبي الدخل الشهري ؟ .
الحل :
1: نفرض أن الدخل الشهري = س

2: نضع التناسب التالي ـــــــــ = ــــــــ
س× 40= 860× 100=86000
إذن :
س= 86000 ÷ 40= 2150
إذن الدخل الشهري = 2150 ريالاً
وهكذا أن الفكرة في النموذج الجديد لحل المسائل المتعلقة بالنسبة المئوية تعتمد اساساً على معرفة قيمة المربع الصغير و الأمثلة التالية توضح كيفية استخدام المربع الكبير في حل العديد من المسائل المتعلقة بالنسبة المئوية وطريقة حل مثل هذه الأمثلة كالتالي :
1: تمثيل المعلومات المعطاة .
2: استخدام الرسم لإيجاد ألا جابه على السؤال المطروح .
وهذه الطريقة توضح أهميه فهم المعلومات وتمثيلها بدلا من التركيز على إيجاد الحل بحفظ قاعدة معينه دون فهم .
مثال (4)
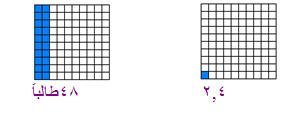
استخدمي المربع الكبير لتمثيل (20%) من الطلاب راسبون في الرياضيات, فإذا كان عدد الطلاب (240) طالباً فكم عدد الراسبين

(2) كم عدد الراسبين في الرياضيات ؟
240 ÷ 100=2.4
أي أن المربع الواحد الصغير يمثل 2.4 وعليه فان (20) مربعا تمثل 20× 2.4=48 طالبا وهم الطلبة الراسبون .
مثال (5)
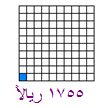
أنفقت شركه ( 12% ) من دخلها السنوي على تحسينات أجرتها على منتجاتها فإذا كان دخلها السنوي 175500 ريال فكم تبلغ النفقات
الحل :

2) كم تبلغ النفقات
175500 ÷100= 1755
أي أن المربع الواحد الصغير يمثل 1755 وعليه فان (12) مربعا تمثل 12 × 1755 = 21.60 ريال وهي قيمة النفقات
بنفس الطريقة السابقة يمكن حل مسائل النسبة المئوية الأكثر صعوبة مثل :
مثال (6)
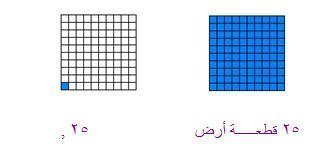
تبرع محسن بـ(25) قطعة ارض واشترط أن يكون منها (6) قطع حدائق عامه فما هي النسبة المئوية للحدائق العامة ؟
طريقة الحل :
(1) تمثيل المعلومات المعطاة على المربع الكبير
نمثل الخمسة والعشرين قطعة ارض على المربع الكبير وبالتالي تكون قيمة المربع الصغير 25÷ 100=0.25
(2) كم عدد المربعات التي تمثلها (6) قطع .
إذا كان المربع الصغير يمثل ربع قطعة أرض فان كل(4) مربعات صغيرة تمثل أرضاً واحدة وبالتالي فان (6) قطع تمثل(24) مربعا على النحو التالي .

وبالتالي فان النسبة المئوية للحدائق العامة 24% .
وبعد هذه ألا مثله التي يمثل فيها المربع الكبير العدد (100) نستعرض بعض ألا مثله التي تكون فيها النسبة اكثر من (100) .
مثال (7)
إذا كان عدد تلميذات المدرسة هذا العام يمثل (135%) من عدد تلميذات العام المنصرم . وكان عدد التلميذات في هذا العام (756) تلميذه فكم عددهن في العام الماضي ؟
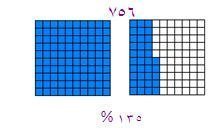
(135%) تمثل 756 تلميذه وعلية فان المربع الصغير يمثل
756÷ 135=5.6 وبالتالي فان :
100 مربع يمثل 5.6× 100 =560 تلميذة
أي أن عدد تلميذات العام المنصرم =560 تلميذة .
مثال (8)
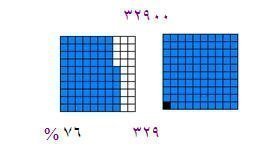
إذا كانت أرباح أحد المحلات في هذه ألسنه 32.900 ريال فإذا زادت الأرباح بنسبة 76% فكم كانت أر باح ألسنه التالية ؟
يمكننا تمثيل الأرباح بالمربع الكبير . وعليه فان (100) مربع تمثل الأرباح الحالية أي 32.900 وبالتالي فالمربع الصغير يمثل 32.900 ÷ 100 =329 أما الأرباح تمثل 76 مربعا في ألسنه التالية هي 76 × 329= 25004 ريال .
وعليه فان إجمالي الإرباح =
32900+ 25004= 57904 ريالاً
والرسم التالي يوضح الفكرة :
مثال (9)
تعتبر التخفيضات من التطبيقات على دروس النسبة المئوية فإذا أعلنت إحدى المكتبات عن تخفيضات قدرها 30% على الأقلام .وكان سعر القلم قبل التخفيض (95) ريال فكم يكون سعر القلم بعد التخفيض ؟
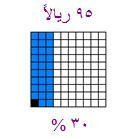
المربع الكبير =95 وبالتالي :
المربع الواحد = 95÷ 100 =0.95 ريال
وبالتالي فان (30) مربعا = 0.95 × 30=28.5
وتطرح من قيمة القلم الأساسي
وعليه يصبح السعر الجديد بعد التخفيض 95- 28.5 = 66.5 .
مثال (10)
كان سعر أحد الأثواب (60) ريالاً ثم أعلن صاحب المحل عن تخفيض على سعر هذا الثوب بما مقدار (20%) . فكم يكون سعر هذا الثوب بعد التخفيض ؟
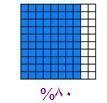
المربع الواحد =60 ÷ 100=0.6 ريال
نحسب قيمة الثوب بعد تخفيضه (20%) من سعره أي أن المبلغ المدفوع في هذه الحالة هو (80%) وهو ما يعادل (80) مربعًا صغيراً ومن ثم فان سعر الثوب بعد التخفيض هو:
80× 0.60= 48 ريال
مثال (11)
إذا أعلنت إحدى المكتبات عن تخفيض قدره(10%) على سعر أحد الأقلام فإذا دفع رجل (99) ريالا ثمنا للقلم بعد التخفيض فكم كان سعره قبل التخفيض ؟
هذا النوع من التطبيقات على النسبة المئوية تحدد فيه قيمة السلعة بعد تخفيض معين والمطلوب معرفة السعر قبل التخفيض .
وعليه فما دفعه الرجل يمثل (90%) من القيمة ألا صليه للقلم .وبالتالي فان :
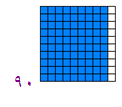
مربعا صغيرا تمثل 99ريال
والمربع الصغير يمثل 99÷ 90=1.1
والمربع الكبير يمثل 1.1× 100=110
مثال (12)
اشترى رجل أرضا بمبلغ معين ثم باعها بمبلغ 650000 ريال فإذا ربح 325% من سعر الأرض فبكم اشتراها ؟
قد يكون هذا النوع من التطبيقات من اصعب الأنواع وبالرغم من ذلك يمكن حلها بنفس الطريقة على النحو التالي :
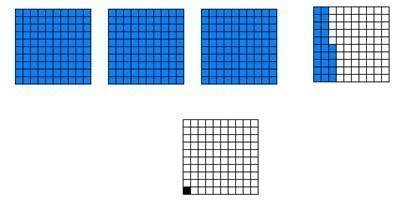
وبالتالي فان 325 مربعا تمثل سعر البيع أي أن كل مربع يساوي 650000÷ 325=2000
وبالتالي فالسعر الأصلي هو 2000×100=200000