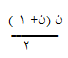
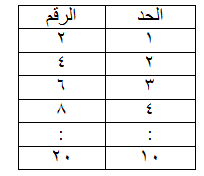
مجموعة الأعداد
يمكن تقسيم الأعداد إلى مجموعتين لتسهيل دراستها وهتين المجموعتين هما
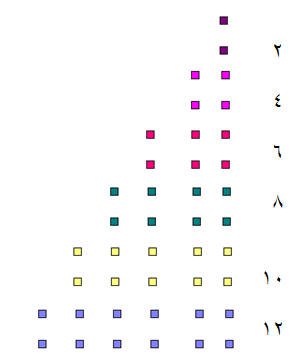
أولاً : الأعداد الزوجية

هل يمكن توزيع كل مجموعة إلى صفين متساويين في العدد ؟ لماذا ؟
مثلاً : العدد 10 يتم تقسيمه على 2 فنجد أنه ينقسم إلى خمسة مجموعات تحتوي كل مجموعة على مربعين ، وليس هناك باقي
أي : -
10 ÷ 2 = 5
إذن العدد 10 عدد زوجي


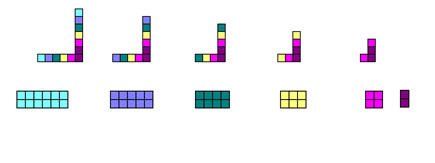
يمكن تمثيل الأعداد الزوجية بقطع دينز كحرف ل أ و كمستطيلات أحد بعديها 2 :
2 × 1
2× 2
2 × 3 …… وهكذا
ما هو الحد العاشر الزوجي ؟
لابد من معرفة القاعدة العامة للأعداد الزوجية من أجل معرفة الحد العاشر الزوجي
نعلم أننا نستطيع تمثيلها بقطع دينز كالتالي

نحصل على مستطيل مكتمل أحد بعديه 2 وعدد القطع في كل صف كالتالي
الأول ( 1 ، 1 )
الثاني ( 2 ، 2 )
الثالث (3 ، 3 )
الرابع ( 4 ، 4 ) .. وهكذا
العاشر ( 10 ، 10 )
بالتالي
القانون العام لإيجاد الأعداد الزوجية = 2 ن
للتأكد إذن ن = 2ن
للتأكد
الحد الأول = 2 (1) = 2
الحد الثاني = 2 (2) = 4
الحد الثالث = 2 (3) = 6
الحد لرابع = 2 (4) = 8
وهكذا
الحد العاشر = 2 (10 ) = 20
بالتالي الحد الزوجي العاشر = 20
ما هو مجموع الأعداد الزوجية ؟
لو أردنا جمع الحد الأول + الحد الثاني ( ح1 + ح2 ) = ؟

نحصل على مستطيل 2 × 3
لو أردنا جمع الحد الأول + الحد الثاني + الحد الثالث ، ( ح1+ ح2 +ح3 )= .....؟

نحصل على مستطيل 3 × 4
لو أردنا جمع الحد الأول + الحد الثاني + الحد الثالث + الحد الرابع ، ( ح1 +ح2 + ح3 +ح4)= .......؟

نحصل على مستطيل 4 × 5 وهكذا .
بالتالي :
ح1 + ح2 = مستطيل ( 2 × 3 )
ح 1 + ح2 + ح3 = مستطيل ( 3 × 4 )
ح1 + ح2 + ح3 + ح 4 = مستطيل ( 4 × 5 )
وهكذا 000000
لو أردنا جمع الحدود من الحد الأول إلى الحد العاشر يكون
ح1 ح10 = مستطيل ( 10 × 11 ) = 110
![]() وهو
نفس الناتج لو استخدمنا قانون
وهو
نفس الناتج لو استخدمنا قانون

مجموع الحدود العشرة الزوجية الأولى
=
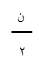 (
الحد الأول + الحد
الأخير )
(
الحد الأول + الحد
الأخير )

=
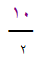 ( 2 + 20 ) = 5 (22) = 110
( 2 + 20 ) = 5 (22) = 110
___________________________________---
ثانياً : الأعداد الفردية
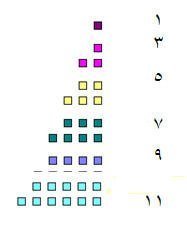
هل يمكن توزيع كل مجموعة إلى صفين متساويين في العدد؟ لماذا
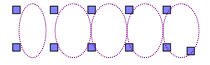
مثلاً :
لنتعرف على العدد 11 هل هو العدد الفردي أي هل إذا قسم على 2 كان ناتج القسمة بباقي .
11 ÷ 2 = 5 والباقي 1
نحصل على خمسة مجموعات في كلاً منها مكعبين ويبقى لدينا مكعب واحد بالتالي هو عدد فردي
بالتالي

يمكن تمثيل الأعداد الفردية كحرف ل أو مستطيلات غير مكتملة كالتالي :
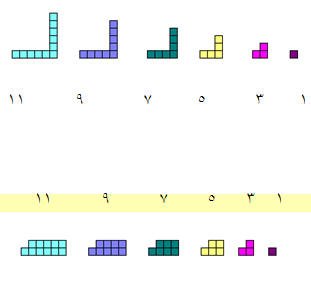
ما هو الحد العاشر الفردي ؟
من أجل معرفة الحد العاشر الفردي لابد من معرفة القاعدة العامة للأعداد الفردية نعلم أننا نستطيع تمثيل الأعداد الفردية بقطع دينز كالتالي :

وكأني ابني مستطيل غير مكتمل أحد بعديه 2 وعدد القطع في كل صف
الأول ( 1 ، 0 )
الثاني ( 2 ، 1 )
الثالث ( 3 ، 2 )
الرابع ( 4 ، 3 )
العاشر(10 ، 9 )
بالتالي :
القانون العام لإيجاد الأعداد الفردية = ( 2ن – 1 )
بالتالي ن = 2ن – 1
للتأكد :-
الحد الأول = 2 (1) –1 = 1
الحد الثاني = 2 (2) –1 = 3
الحد الثالث = 2 (3) –1 = 5
الحد الرابع = 2 (4) – 1 = 7
وهكذا 00000000000
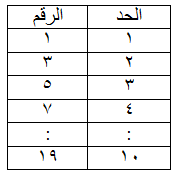
أذن الحد العاشر = 2 ( 10 ) – 1 = 19
بالتالي الحد الفردي العاشر = 19
ما هو مجموع الأعداد الفردية ؟
لو أردنا جمع الحد الأول + الحد الثاني, ( ح1 + ح2 ) = ....؟

نحصل على مربع طوله 2 وعرضه 2 ومساحته = 2× 2 = 2 =4
لو أردنا جمع الحد الأول + الحد الثاني + الحد الثالث, ( ح1 +ح2+ح3)= .....؟
نحصل على مربع طوله 3 وعرضه 3 ومساحته = 3× 3= 3 = 9
لو أردنا جمع الحد الأول + الحد الثاني + الحد الثالث + الحد الرابع , (ح1+ح2+ح3+ح4)=؟
نحصل على مربع طوله 4 وعرضه 4 ومساحته=4×4 =24= 16
بالتالي
ح1 + ح2 = 2
ح1 + ح2 + ح3 = 3
ح1 + ح2 + ح3 + ح4 = 4
ح1 + ح2 + ح3 + ح4 + ح5 = 5
ولو أريد جمع الحدود من الحد الأول إلى الحد العاشر يكون =210 = 10 × 10 = 100
وهو نفس الناتج استخدمه القانون
مجموع الحدود العشرة الأولى الفردية
![]()
=
 ( الحد الأول + الحد الأخير )
( الحد الأول + الحد الأخير )

=
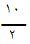 ( 10 + 19 )
( 10 + 19 )

=
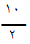 (20 ) = 5×20= 100
(20 ) = 5×20= 100
وهو نفس الناتج السابق .
مجموع العشرة حدود الأولى ( الزوجية , الفردية )
نعلم أن مجموع العشرة حدود الزوجية الأولى = 110
ونعلم أن مجموع العشرة حدود الفردية الأولى = 100
ولإيجاد مجموع العشرة حدود من الأعداد المتتالية يمكن إيجادها بالقانون السابق :
 ـــــ
( ح1 + ح2 ) = ـــــ ( 1 + 10 ) = 5 ( 11 ) = 55
ـــــ
( ح1 + ح2 ) = ـــــ ( 1 + 10 ) = 5 ( 11 ) = 55
يمكن أن نجعل التلميذة تستنتج العلاقة بنفسها :-
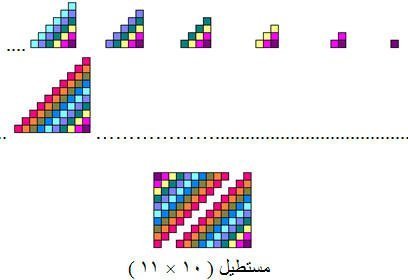
عند جمع عشرة حدود متتالية احصل على الشكل السابق وإذا كررة نفس الشكل وقمة بنقلة احصل على مستطيل ( 10 × 11 )
مساحته = 10 × 11 = 110
 وإذا
أردن مجموع الحدود العشرة المتتالية مرة واحدة فقط بالتالي :
وإذا
أردن مجموع الحدود العشرة المتتالية مرة واحدة فقط بالتالي :
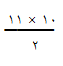 =
= 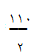 = 55
= 55
بالتالي فإن مجموع العشرة حدود المتتالية = 55
وهو نفس الرقم الذي حصلنا عليه من القانون السابق .

وتكون الصيغة العامة لمجموع الأعداد المتوالية على النحو التالي :