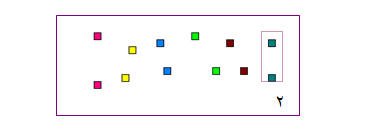
العدّ

لقد اطلع العرب على حساب الهنود فأخذوا عنه نظام الترقيم، إذ أنهم رأوا أنه أفضل من النظام الشائع بينهم وكان لدى الهنود أشكال عديدة للأرقام، هذب العرب بعضها وكونوا من ذلك سلسلتين، عرفت إحداهما بالأرقام الهندية وهي التي تستعملها هذه البلاد وأكثر الأقطار العربية والإسلامية وهي ( 1 , 2 , 3 , 4، 5 , 6 , 7 , 8 , 9 ) وعرفت الثانية بالأرقام الغبارية  ، وقد انتشر استعمالها في بلاد الغرب والأندلس، وليس المهم هنا تهذيب العرب للأرقام وتوفيقهم في اختيار هاتين السلسلتين أو إدخالهما إلى أوربا بل المهم هو إيجاد طريقة جديدة لها وهي طريقة الإحصاء العشري ، واستعمال الصفر لنفس الغاية التي نستعملها الآن .

وكان الهنود يستعملون ( سونيا ) أو الفراغ لتدل على معنى الصفر، ثم انتقلت هذه اللفظة الهندية إلى العربية باسم ( الصفر ) ومن  المعروف أن لأرقام الرومانية أشكال عديدة بحيث يصعب تعلمها بسهولة ، ولما جاء العرب شعروا بصعوبتها فنقبوا في الأرقام الهندية فوجدوا أن فكرتها أفضل بكثير من السابقة فأخذوا عن الهنود أرقامهم بعد أن طوروها وشذبوها لتكون أكثر فعالية ، ولهذه الأرقام العديد من المزايا منها.

أنها تقتصر على عشرة أشكال بما فيها الصفر، ومن هذه الأشكال يمكن تركيب أي عدد مهما كان  كبيرا بينما الأرقام الرومانية تحتاج إلى أشكال عديدة وتشتمل على أشكال جديدة للدلالة على بعض الأعداد ومن مزاياها أيضا أي الأرقام العربية أو الهندية  أنها تقوم على النظام العشري، وعلى أساس القيم الوضعية بحيث يكون للرقم قيمتان: قيمة في نفسه، كقيمة الأربعة في العدد 4 ، وقيمة بالنسبة إلى المنزلة التي يقع فيها، كقيمة الثلاثة في العدد 234 وهي ثلاثين ولعل من أهم مزايا هذا النظام هو إدخال الصفر في الترقيم واستعماله في المنازل الخالية من الأرقام ، ولسنا بحاجة إلى أنه لولا الصفر واستعماله لما فاقت الأرقام العربية والهندية غيرها من الأرقام ولما كانت لها أية ميزة ، بل لما فضلتها الأمم على الأنظمة الأخرى المستعملة في الترقيم .

وللصفر فوائد أخرى، فلولاه لما استطعنا أن نحل كثيرا من المعادلات الرياضية من مختلف الدرجات بالسهولة التي نحلها بها الآن، ولما تقدمت فروع الرياضيات تقدمها المشهود ، وكذلك لم تتقدم المدنية هذا التقدم العجيب .

  الترتيب والتسلسل 

من الضروري أن تفهم التلميذة العلاقة بين الترتيب ( التصنيف ) فعند عندها للأشياء يجب أن ترتبها حتى تتمكن من عد كل شئ على حدة .

وسيتم ترتيب ( تصنيف ) الأشياء حسب الحجم ، الطول ، اللون وهكذا .

" ولقد أكد بياجيه على أن الترتيب يقود لمعرفة العدد وأن معرفة العدد يقود إلى الترتيب "

   الأعداد من 1 – 9

ويمكن تقديم طريقة العد بثلاثة طرق :

( أ ) التصنيف :

نعرض مجموعة من قطع دينز ونطلب من التلميذات تصنيفها إلى مجموعات لها العدد نفسه من القطع  .

مثال (1)

كون مجموعات عدد عناصر كل مهنا يساوي عدد عناصر المجموعة المعطاة ثم اكتبي العدد :-

نلاحظ هنا التلميذة بأن كل مجمعة مكونة من وحدتين ذات لون واحد قد ربطة بالعدد (2), وهكذا تتعرف التلميذة على العدد وكتابته ويكون ذلك بطريقة محسوسة وملموسة أمامها وتستطيع عدها ولمسها , وهكذا نفعل مع بقية الأعداد مع بقية الأعداد  .

(ب) العلاقة أكثر بواحد

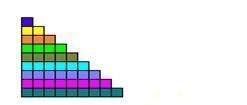
يعرض المعلم قطعة في الو حايد  وتطلق عليها الرقم (1) ثم تضيف عنصر آخر إلى هذه المجموعة بلون مختلف ثم نكتب الرقم

(2) وهكذا مع بقية الأعداد حتى الرقم (9)

ثم يسأل المعلم التلاميذ :

ما هي المجموعة المكونة من عنصرين ؟

ما هي المجموعة المكونة في ثلاثة عناصر ؟

أي المجموعتين أكثر من المجموعة الثانية بواحد ؟

أي المجموعتين أقل من المجموعة الثانية بواحد ؟

( جـ) ملء الأشكال :

كما ذكرنا في السابق يمكن الاستفادة من قطع دينز في تقديم مفهوم العدّ عن طريق ملء الأشكال المرسومة وعدّ القطع المستخدمة في ذلك .

مثال (1)

أملئ الشكل التالي بقطع دينز المناسبة وكم قطعة من الو حايد, الأصابع , المربعات نحتاج .

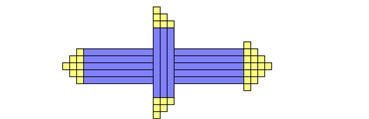
مثال (2)

استخدمي إحدى عشرة قطعة من الأصابع وست عشر قطعة من الوحايد لتغطية الشكل التالي .