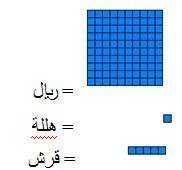
النقود وتحويل النقود
الكثير من التلاميذ يجدون صعوبة في فهم أن
الريـــال = 100 هلله
القـــرش = 5 هلالات
الريـــال = 20 قرشاً
وبإمكان قطع دينز أن تقدم هذا الدرس للتلاميذ بشكل أكثر سهولة بأن نفرض أن :

بالتالي فإن :
الريــــال = 100 هلله
القــــرش = 5 هلالات
الريـــــال = 20 قرشاً
 مثال
(1)
مثال
(1)
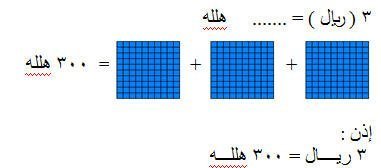
مثال (2)

مثال 3

جمع النقود
مثال (1)
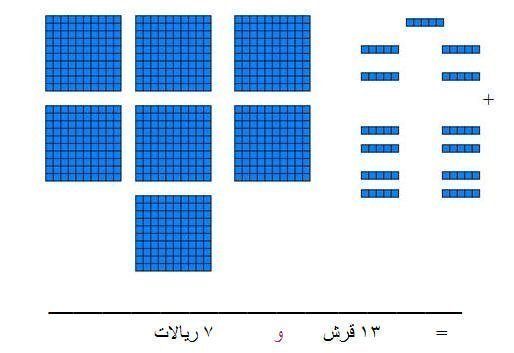
اجمع
5 قروش 3 ريالات
+ 8 قروش 4 ريالات
ـــــــــــــــــــــــــــــــــــــــــــــــــــــ
=
 مثال
(2)
مثال
(2)
12 قرشاً 4 ريالات
+ 8 قروش 5 ريالات
ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
=
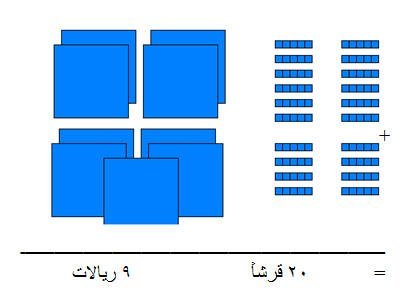
وحيث أن كل 20 قرشاً = (1) ريال , أصبح المجموع الأخير
4 ريالات و 12 قرشاً + 5 ريالات و 8 قروش = 10 ريالات
وهو ما يعرف بتحويل النقود ويأخذ في الصف الثالث ابتدائي .
طرح النقود
 مثال
مثال
اطرح
6 قروش 5 ريالات
- 4 قروش 3 ريـــال
ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
=
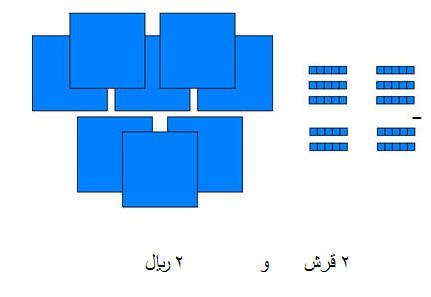
نشاط
(1)
6 ريالات = ............ قرشاً
7 قروش = ............. هللة
5 ريالات = .............هللة
(2)
38 قرشاً = ........ ريال و........ قروش
50 قرشاً = ........ ريال و........ قروش
(3)
اجري عمليات الجمع التالية :-
11 قرشاً 5 ريالات
+ 4 قروش 12 ريال
ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
=............................................
12 قرشاً 8 ريالات
+ 5 قروش 7 ريالات
ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
=.............................................
(4)
اطرحي
18 قرشاً 50 ريال
- 15 قرشاً 27 ريال
ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
=
الضرب
هناك طريقتين يمكن استخدامها لشرح عملية الضرب بقطع دينز.
الطريقة الأولى
في حقيقة الأمر يعتبر الضرب عملية تكرار للجمع لذا لابد من أن تسبق عملية الضرب عملية تمثيل العدد باستخدام مكعبات دينز .
مثال (1)
لضرب 3 × 2
نمثل العدد 3 ( مرتين )

أو
نمثل العدد 2 ( ثلاث مرات )

ونلاحظ أن :-
الناتج هو نفسه في المرتين وهو 6 قطع لأن الضرب عملية أبدالية لا تتأثر بالترتيب .
3 × 2 = 6
2 × 3 = 6
مثال (2)
لضرب 24 × 3 نقول بتمثيل 24 ثلاث مرات كما هو موضح في الشكل التالي :-
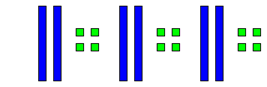
ثم نرتبها في الجدول :
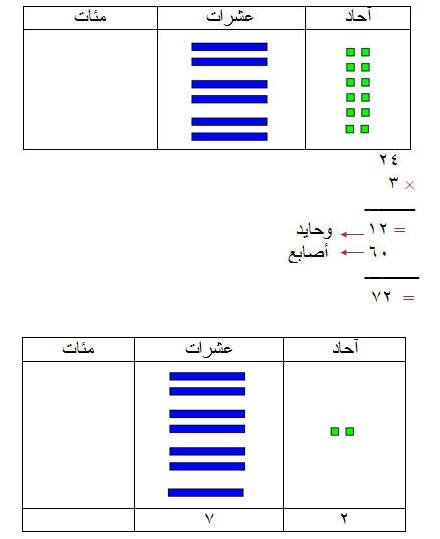
مثال (3)
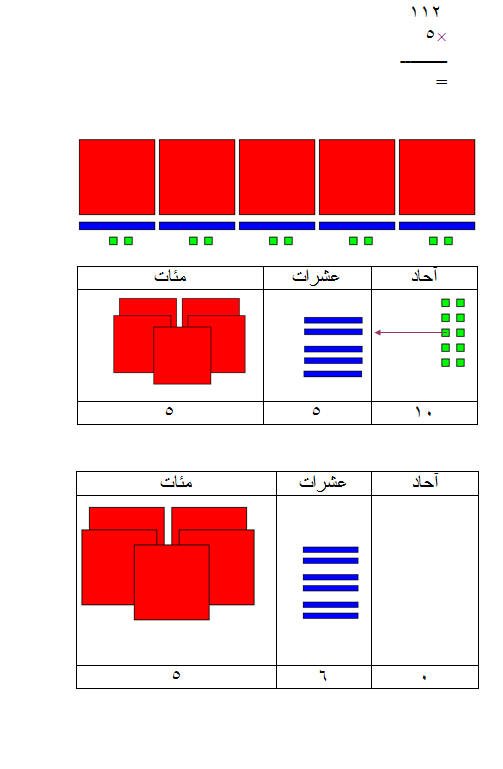
ويمكن تلخيص عملية الضرب في التالي :
1) تمثيل الأعداد .
2) ترتبها في الجدول .
3) جمع الوحايد ومقايضتها بأصبع إذا احتاج الإمر إلى ذلك .
4) جمع الأصابع ومقايضتها بمربع إذا احتاج الأمر إلى ذلك .
5) جمع المربعات ومقايضتها بمكعب إذا احتاج الأمر إلى ذلك .
الطريقة الثانية
نكون مستطيل أحد بعديه أحد العدديين المضروبين في بعضهما والبعد الثاني العدد الثاني المضروب فيه ومساحة هذا المستطيل هي حاصل ضرب هذين العددين.
مثال (1)
6 × 7 = ......
نكون مستطيل احد بعديه 6 والآخر 7 ومساحته تكون ناتج حاصل الضرب كالتالي :
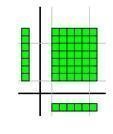
بالتالي يكون ؛-
6 × 7 = 42
مثال (2)
13 × 2 = .......
بالتالي : 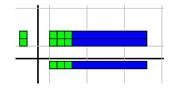
13
× 2
ـــــــــــــ
![]() = 6 وحايد
= 6 وحايد
20 اصابع
ـــــــــــــــ
= 26
مثال (3 )
23 × 32 = .......
