أولاً : التناظر " التماثل "
ينقسم إلى قسمين هما
أ) التناظر حول نقطة 0
ب) التناظر حول محور 0
أ: التناظر حول محور
التناظر : هو التماثل أي إيجاد الشكل المطابق له تماماً
فيمكن أن تردك التلميذة مفهوم التناظر بطريقة محسوسة حيث تتم مقارنة كل قطعة بنظيرتها ومن ثم إيجاد نظير الشكل المكون من عدة قطع
مثال (1)

تقدم المعلمة للتلميذات ورقة رسم عليها خط عمودي في منتصفها يمثل محور التناظر وليكن هنا س ص وتكون في قطع دينز شكلين متناظرين حول هذا المحور فتدرك التلميذة بأن الشكل الأول ينطبق على الشكل الثاني .
مثال (2)
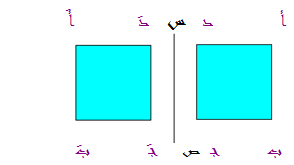
نلاحظ من الشكل السابق :
أن نظير النقطة أ حول محور س ص في المستوى هي النقطة أَََََ وكذلك
أن نظير النقطة ب حول محور س ص في المستوى هي النقطة بَ وكذلك
أن نظير النقطة جـ حول محور س ص في المستوى هي جـَ وكذلك
أن النظير النقطة د حول محور س ص في المستوى هي دَ 0
بالتالي :

مثال (3)
وبعد أن يعرض المعلم على التلميذ مجموعة من الأشكال ونظائرها سوف يستنتج التلميذ أنة :

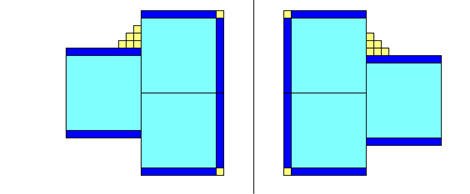
خصائص التناظر حول محور :
من الأمثلة السابقة تستطيع التلميذة أن تستنتج خصائص التناظر حول محور يحافظ :
1- على الأطوال
2- على الزوايا
3- على التعامد
ب - التناظر حول نقطة
يمكن تمثيل التناظر حول نقطة بقطع دينز كما في المثال التالي :
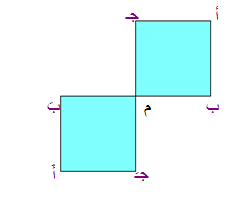
من الشكل السابق ومع المناقشة مع التلميذات أن نستنتج التالي :

خصائص التناظر حول نقطة
1) يحافظ على الأطوال
2) يحافظ على الزوايا
3) يحافظ على التعامد
العلاقة بين التناظر حول محور التناظر حول نقطة
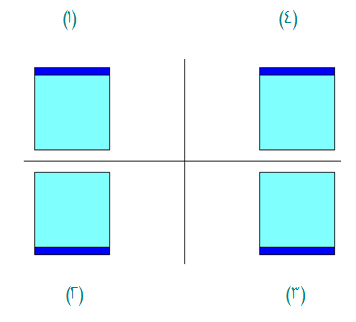
الشكــل(1) بإيجاد نظيره حول النقطة م يكون الشكل (3) .
نظير شكل(1) بالتناظر حول المحور السيني هو الشــكل(3) .
نظير شكل(2) بالتناظر حول المحور الصادي هو الشكـل( 3) .
إذن :


أما التناظر حول المحور الصادي فهو عبارة عن دوران بـ( 180 ْ) أو تناظر حول نقطة وتناظر حول المحور السيني .
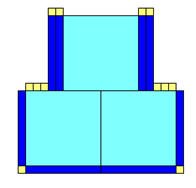
كون الشكل التالي من قطع دينز ثم أوجد نظيره حول محور السينات
 ثانياً
: الإنسحاب
ثانياً
: الإنسحاب
هو نقل الشكل من مكان إلى آخر إلى أسفل أو أعلى أو إلى اليمين أو اليسار ، ويبقى الشكل كما هو 0
ويمكن أو نوضح ذلك بقطع دينز بان نكون من هذه القطع شكل ما ويوضع على سطح مستوى وتتم إزاحة الشكل ( سحبه ) باتجاه معين وبمسافة معينة فنلاحظ أن الشكل الناتج هو نفس الشكل, كما في الشكل التالي :
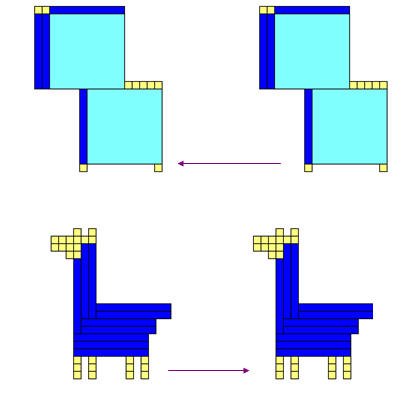
1) المنحنى : ويحدده المستقيم الذي يحصل الانسحاب بموازاته 0
2) ا لاتجاه : وهو طريقة التوجه على المنحنى 0
3) المقياس : وهو المسافة بين نقطة وصورتها بالإنسحاب 0
بالتالي :

ويمكن أن تستنتج التلميذة خصائص الإنسحاب من خلال العرض فنجد أنها تمثل نفس خصائص التناظر 0
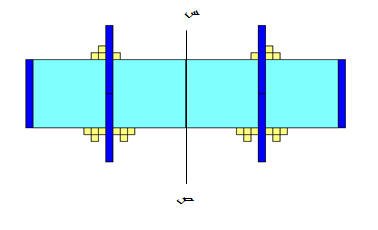
كما يمكن إثبات أن تركيب تناظرين حول محورين متوازيين هو انسحاب كما في الشكل التالي :
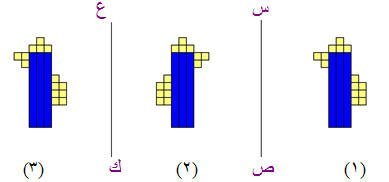
وهو نفسه الانسحاب للشكل (1) فنحصل على الشكل (3)
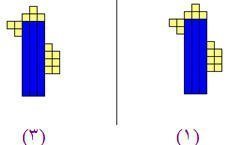
أي الأشكال التالية أجرينا عليها انسحاب
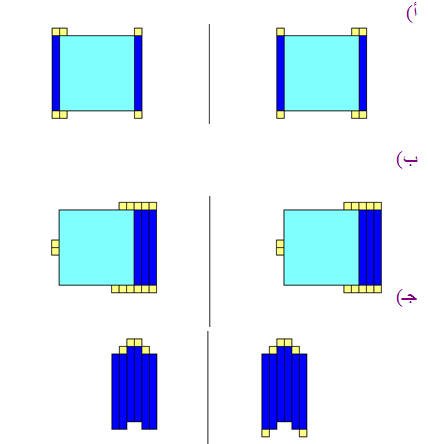
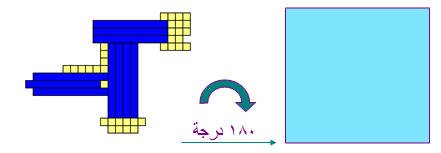
ثالثاً : الدوران
هو تدوير الشكل حول نقطة معينه بمقياس محدد ( زاوية معروف مقدارها ) في أحد الاتجاهين الموجب أو السالب 0
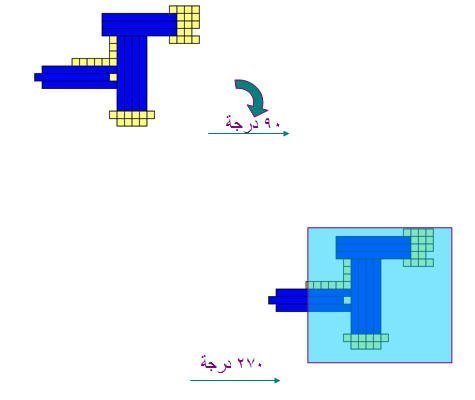
ويمكن توضيح ذلك بقطع دينز حيث نكون شكل ونضعه على سطح مستوى ثم نجري لهذا الشكل دوران بمقدار معين في أحد الاتجاهات كما في الأشكال التالية :
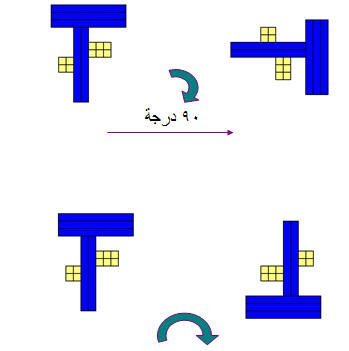
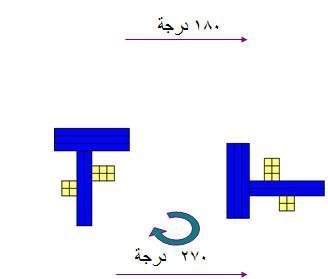
كما يمكن للتلميذات استنتاج أن الدوران ما هو إ‘لا تناظر حول محورين متعامدين و ن مركز الدوران زاويته ضعف الزاوية بين المحورين 0
كما في الشكل التالي :
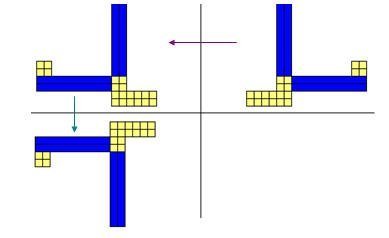
نشاط
(1) أجري دوران للأشكال التالية في اتجاه عقارب الساعة :