 مثال
(1)
مثال
(1)
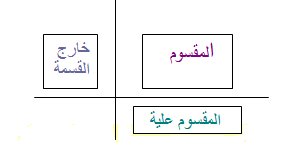
القسمة
الطريقة الأولى
يمكن أن نعتبر القسمة على أنها تجزئه المقسوم إلى عدد مرات المقسوم عليه ( أجزاء متساوية ) ومعرفة العدد الناتج . وهي عملية عكسية للضرب أوهي عملية طرح متكرر .
 مثال
(1)
مثال
(1)
6 ÷ 2 = .......
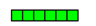
كم عدد القطع التي نحص عليها في كل مجموعة لو قسمنا الستة ألي جزئيين متساويين ؟

خارج قسمة 6 ÷ 2 = 3
وبنفس الطريقة يمكن قسمة
6 ÷ 3 = .......

خارج قسمة 6 ÷ 3 = 2
وهي قسمة بدون باقي قاعدتها تعرف كالتالي :-
المقسوم ÷ المقسوم عليه = خارج القسمة
ويمكن التأكد من هذه القسمة في القانون
المقسوم = المقسوم عليه × خارج القسمة
6 = 2 × 3 في الحالة الأولى
6 = 3 × 2 في الحالة الثانية
مثال (2)
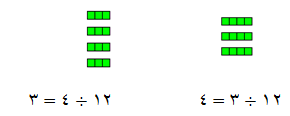
وللتأكد من الناتج :
12 = 4 × 3 أو 12 = 3 × 4
 مثال
(3)
مثال
(3)
13 ÷ 3 = ......
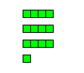
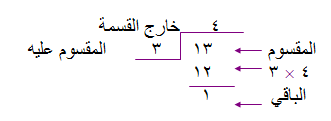
مثال ( 4 )
9 6 3 ÷ 3 = ......
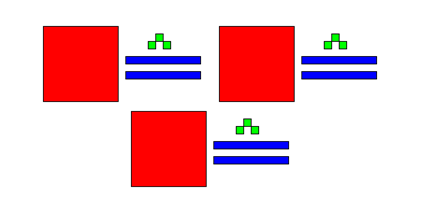
÷ 3 = ( 9 + 60 + 300 ) ÷ 3
300 ÷ 3 = 100 , 60 ÷3 = 20 , 9÷3=3
100 + 20 + 3 = 123
ثم نعلم التلميذ العملية هذه :-
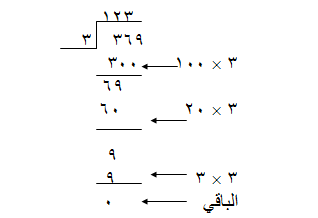
مثال (5 )
453 ÷ 3 = ……
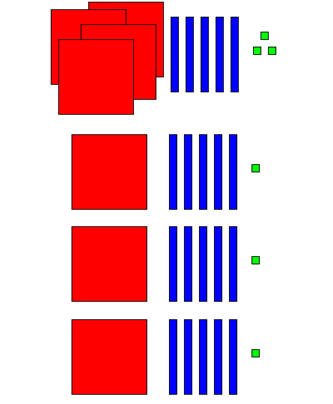
453 ÷ 3 = (3 + 50 + 400 ) ÷ 3
=( 3 + 150 + 300 ) ÷ 3 ( بعد فك المائة )
=( 3 ÷ 3 )+( 150 ÷ 3 )+( 300 ÷ 3 )
= 1 + 50 + 100
= 151
يمكن القيام تمثلها عل النحو التالي :
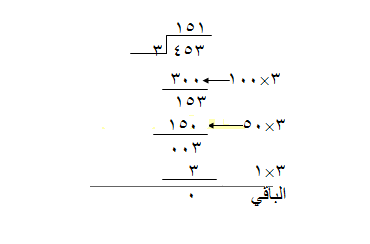
وللتأكد من عملية القسمة نعوض في القاعدة :
المقسوم = المقسوم عليه × خارج القسمة + الباقي
453 = 3 × 151
= 453
الطريقة الثانية
لقسمة عدديين علينا تمثل المقسوم والمقسوم عليه ثم بناء مستطيل أحد بعديه المقسوم عليه ومساحة هذا المستطيل تساوي المقسوم وهذه الطريقة تقرب مفهوم المساحة أي حاصل ضرب البعدين تعطي المساحة الداخلية وهي هنا المقسوم .
 مثال
(1)
مثال
(1)
9 ÷ 3 =.......
نبني مستطيل مساحته 9 واحد بعدية 3 كالتالي :
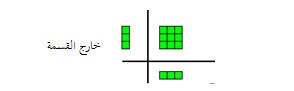
بالتالي فإن خارج القسمة كما هو واضح من الرسم = 3
مثال (2)
276 ÷ 23 = ......
نمثل 276
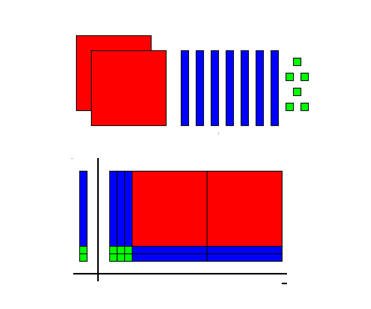
بالتالي فإن خارج القسمة = 12
276 ÷ 23 = 12
وهي قسمة بدون باقي
مثال (3)
105 ÷ 5 = ……
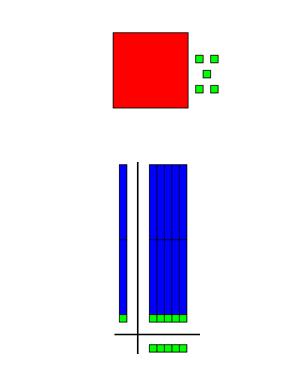
لجئنا هنا لفك المائة إلى 10 أصابع وفك الثلاث أصابع إلى وحايد ثم أضفنا 2 من الو حايد الموجودة سابقا لإكمال بناء المستطيل وعلية
105 ÷ 5= 21
مثال (4)
42 ÷ 10 = ……
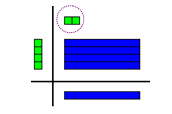
وعملية 42 ÷ 10 = 4 والباقي 2
مثال (5)
272 ÷ 11= ……
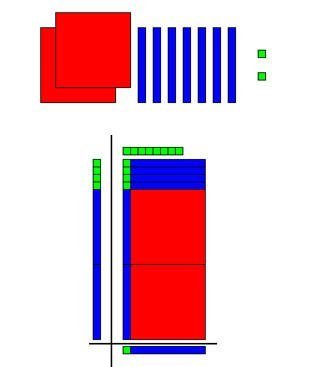
وعملية 272 ÷ 11 = 24 والباقي 8
وللتأكد من صحة القسمة نعوض في نفس القاعدة السابقة
المقسوم = المقسوم عليه × خارج القسمة + الباقي
272 = 11 × 24 + 8
= 264 + 8
= 272
 نشاط
نشاط
أوجد عمليات القسمة التالية :
(1) 15 ÷ 3 = .......
(2) 132 ÷ 12 = .......
(3) 60 ÷ 24 = .......