المتطابقات

يستفاد  من اللوحة الملونة أيضا في تدريس العديد من المتطابقات وخصوصاً بعد أن فهم الطالب عمليات الجمع والطرح والضرب والقسمة  والمساحات ومفهوم بقاء المساحة  حيث يستفيد منها في حل المتطابقات

أمثلة لبعض المتطابقات:

الفرق بين مربعين

س2 – ص2

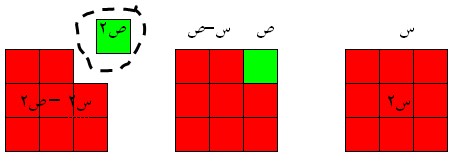
كما يتضح من الشكل أن المربع الأحمر طول ضلعه س  أي مساحته س2

والمربع الأخضر طول ضلعه ص أي مساحته ص2

وفي حالة الطرح  نستقطع الجزء الأخضر من الأحمر  والجزء المتبقي 

هو  س2 – ص 2

ومن مفهوم بقاء المساحة فإن الطالب يستطيع نقل الضلع س - ص  ليكون شكل مستطيل كما في الشكل

حيث المستطيل الناتج طوله س + ص  وعرضه س-ص

فتكون مساحته (س + ص) ( س – ص )

أي أن

مربع مجموع حدين

(س + ص ) 2

يمكن توضيحها باستخدام اللوحة الملونة برسم مربع طول ضلعه س + ص

كما في الشكل التالي :

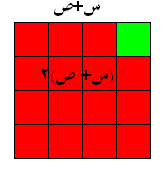
فالشكل الكلي مربع طول ضلعه س+ص  فتكون مساحته (س+ص)2

ومن مفهوم بقاء المساحة فإن مساحة المربع تساوي مجموع مساحات الأجزاء المكونة له والتي كما يتضح مساحاتها

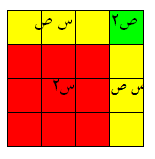
س2  ، س ص ، س ص  ، ص2

أي أن :

(س+ص)2 = س2 + 2س ص + ص2