9        مفهوم العدد الزوجي والعدد الفردي

إن نظرية العدد فرع قديم من فروع الرياضيات، وتبنى على العمليات الأساسية، وتتضمن أنماطاً وعلاقات بين الأعداد، وقد تدّرس للتلاميذ ويستظهروها بشكل آلي، وقد تمر بعض المفاهيم التي يجب

 

 أن يدركها التلاميذ بإتقان، لكي يبنى عليها مفاهيم وحقائق وتعميمات أكثر تعقيداً، و من المفيد للمعلمين أن يكونوا ملمين ببعض الأفكار عن نظرية العدد مثل العدد الفردي والزوجي والعدد الأولي والعدد

 

 غير الأولي وغيرها.

أ- مفهوم العدد الزوجي والعدد الفردي:  

  يقدم مفهوم العدد الزوجي على أنه عدد يقبل القسمة على 2 دون باق، ويقدم العدد الفردي على أنه عدد لا يقبل القسمة على 2 دون باق.

 

 

  لمعرفة العدد 8 أن كان زوجياً أم فردياًً، تشكيل قطاراً من القطع الحمراء أسفل القطعة البنية، فإذا تطابقت أطوال القطع الحمراء مع القطعة البنية يكون العدد 8 زوجي، وإن لم تتطابق يكون العدد 8 فردي.

         

                                

 

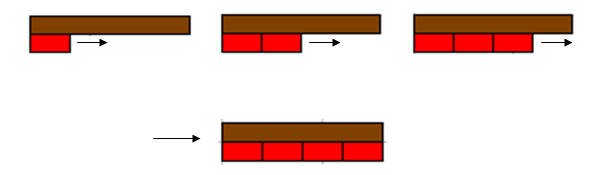
من الملاحظ أن أربعة قطع حمراء تطابقت مع قطعة واحدة بنية لذلك العدد (8) عدد زوجي.

ولمعرفة العدد 5 أن كان فردياً أم زوجياً، تشكيل قطاراً من القطع الحمراء أسفل القطعة الصفراء، فإذا تطابقت أطوال القطع الحمراء مع القطعة الصفراء  يكون العدد 5 زوجي، وإن لم تتطابق يكون العدد 5 فردي.

                                   

                                      

من الملاحظ أن القطعتين ذات اللون الأحمر تقل عن القطعة الصفراء، وإذا وضعت قطعة ثالثة تزيد عن الصفراء. أي أن العدد (5) هو عدد فردي.

 

فبهذه الطريقة يمكن معرفة بقية الأعداد الزوجية والفردية , فلمعرفة العددين (14 ,15) أيهما الزوجي وأيهما الفردي , يتّبع الآتي :

 

                                 أولاً :  تمثيل العدد 14

 

                  

                       ثم تشكيل قطاراً من القطع الحمراء بأسفله

                  

من الملاحظ أن القطع الحمراء تطابقت مع قطع العدد14 فذلك يعني أن العدد14يقبل القسمة على2بدون باقٍ

                            إذاً فالعدد 14 هو عدد زوجي .

 

 

 

                                ثانياً : تمثيل العدد 15

 

               

                      ثم تشكيل قطاراً من القطع الحمراء أسفله

 

            

          من الملاحظ أن القطع الحمراء زادت ولم تتطابق مع قطع العدد 15

 

               

                      والملاحظ هنا أنها نقصت ولم تتطابق أيضاً

                فذلك يعني أن العدد 15 لايقبل القسمة على 2 بدون باقي

                            إذاً فالعدد 15 هو عدد فردي .