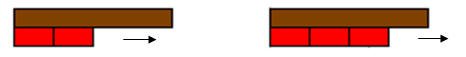7          القسمة بدون باقٍ

 يقدم مفهوم القسمة عن طريق تجزئة المقسوم إلى مجموعات جزئية متساوية، بحيث يكون عدد عناصر كل مجموعة يساوي المقسوم عليه، وناتج القسمة هو عدد المجموعات الجزئية المتساوية،

وقد يقدم المفهوم على أنه طرح متكرر لنفس مقدار المقسوم عليه، أو يمكن تقديمها على أنها عملية معاكسة لعملية الضرب، يمثل المقسوم حاصل ضرب ناتج القسمة والمقسوم عليه.

                            أولاً : القسمة بدون باقِ :

                                   لقسمة 8 ÷ 2 =

ومعنى ذلك : الثمانية كم فيها اثنين أو كم اثنين توجد في الثمانية

ولتمثيل ذلك بأخذ القطعة بنية اللون لتمثيل المقسوم وهو العدد (8) .

                                                                                          

ثم أخذ القطعة الحمراء لتمثيل المقسوم عليه وهو العدد (2) .

ثم وضع القطعة الحمراء أسفل القطعة البنية من الناحية اليسرى .

و تكرار وضع القطع الحمراء تحت القطعة البنية...       

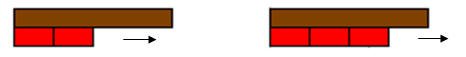
إلى أن تساوى مجموعة القطع الحمراء مع القطعة البنية في الطول.

فنسأل السؤال التالي : من كم قطعة حمراء تتكون القطعة البنية؟

 فيكون الجواب : (4 قطع حمراء) ,أي أن القطعة البنية يمكن أن تتجزأ إلى (4قطع حمراء) .

                          مما يعني أن    8 ÷ 2 = 4

فنسأل السؤال التالي : من كم قطعة حمراء تتكون القطعة البنية؟

 فيكون الجواب : (4 قطع حمراء) ,أي أن القطعة البنية يمكن أن تتجزأ إلى (4قطع حمراء) .

                          مما يعني أن    8 ÷ 2 = 4

                    كما يمكن تمثيل 8 ÷ 2 =

بطريقة أخرى وهي : طرح متكرر من المقسوم بمقدار المقسوم عليه .

بأخذ القطعة البنية لتمثيل المقسوم وهو العدد (8) .

ثم أخذ القطعة الحمراء لتمثيل المقسوم عليه (2) .

ثم تغطية القطعة البنية (المقسوم) بقطع من الحمراء (المقسوم عليه) .

  بقطعة

ثم  بقطعتين

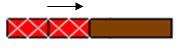
ثم بثلاث قطع

   حتى يتم تغطيتها بالكامل

فنسأل السؤال التالي : كم قطعة حمراء استخدمنا لتغطية القطعة البنية بالكامل؟

                             فيكون الجواب : (4 قطع حمراء) .

                  أي أن القطعة البنية يمكن أن تتجزأ إلى (4قطع حمراء) .

                             مما يعني أن    8 ÷ 2 = 4

 

 

ولقسمة    8 ÷ 4 =

بأخذ القطعة البنية لتمثيل المقسوم وهو العدد (8) .

                                                                           

                 ثم أخذ القطعة الزهرية لتمثيل المقسوم عليه وهو العدد (4) .                

                                                                                                      

                  تكرار وضع القطع الزهرية تحت القطعة البنية...

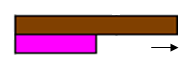
              إلى أن تساوى مجموعة القطع الزهرية مع القطعة البنية في الطول.               

               فنجد أن القطعة البنية يمكن أن تتجزأ إلى (قطعتين زهريتين) .

                       مما يعني أن 8 ÷ 4 = 2

كما يمكن تمثيل 8 ÷ 4 =

بطريقة: الطرح متكرر من المقسوم بمقدار المقسوم عليه .

                    بأخذ القطعة البنية لتمثيل المقسوم وهو العدد (8) .

                         

              ثم أخذ القطعة الزهرية لتمثيل المقسوم عليه وهو العدد (4) .                

                                    

        و بتغطية القطعة البنية (المقسوم) بقطع من الزهرية (المقسوم عليه) .

                                   

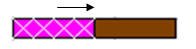
          من الملاحظ احتجنا إلى قطعتين زهريتين لتغطية القطعة البنية بالكامل

                              مما يعني أن 8 ÷ 4 = 2

ولقسمة    27 ÷ 9 =

           بأخذ قطعتين برتقالية وقطعة سوداء لتمثيل المقسوم وهو العدد (27)

               ثم أخذ القطعة الزرقاء لتمثيل المقسوم عليه وهو العدد (9) .                

                            

              ثم تكرار وضع القطع الزرقاء تحت القطع الممثلة للعدد(27)..

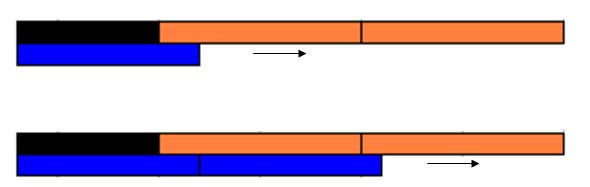
         إلى أن تساوى مجموعة القطع الزرقاء مع القطع الممثلة للعدد(27) في الطول.                

          من الملاحظ أن القطع الممثلة للعدد(27) يمكن أن تتجزأ إلى (ثلاث قطع زرقاء) .

                       مما يعني أن 27 ÷ 9 = 3

كما يمكن تمثيل 27 ÷ 9 =

بطريقة: الطرح متكرر من المقسوم بمقدار المقسوم عليه .

               بأخذ قطعتين برتقالية وقطعة سوداء لتمثيل المقسوم وهو العدد (27)

    

                 ثم أخذ القطعة الزرقاء لتمثيل المقسوم عليه وهو العدد (9) .                

                            

           وتغطية المقسوم (27) بقطع من الزرقاء المقسوم عليه(9) .

                                           بقطعة

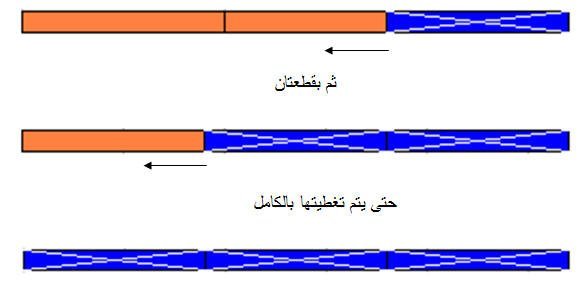
من الملاحظ احتجنا إلى ثلاثة قطع زرقاء لتغطية العدد(27) بالكامل

                              مما يعني أن 27 ÷ 9 = 3

 

لقسمة 56 ÷ 8 =

وضع مجموعة من القطع بنية اللون على شبكة التربيع ، إلى أن تكون مستطيلاً أحد أطوال ضلعيه (8) ومجموع المربعات التي تغطيها (56) مربعاً من مربعات شبكة التربيع .

                                                  

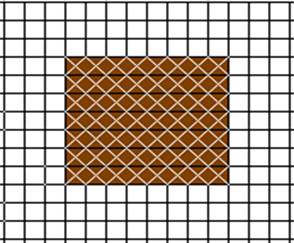
بما أن القطعة البنية (8) تمثل أحد أبعاد المستطيل الظاهر بالشكل , حيث أنها اشتملت على ثمانية أعمدة  , لتغطية (56) مربعاً .

إذاً : كم عدد القطع البنية التي تم استخدامها لتغطية (56) مربعا على شبكة التربيع ؟

أو ماهو عدد الصفوف التي شملتها هذه القطع كما في الشكل السابق؟

أو ماهو البعد الآخر لهذا الشكل ؟ أي كم مربعاً طول الضلع الآخر للشكل ؟             

فيكون الجواب :7قطع أو 7 صفوف أو 7 مربعات .

                       وهذا يعني أن  56 ÷  8  = 7