نظرية
العدد
نظرية
العدد فرع
قديم جداً من
فروع
الرياضيات
وتبنى على
العمليات
الأساسية
وتتضمن أنماطاً
وعلاقات بين
الأعداد .
ومن
المفيد
للمعلمين أن
يكونوا ملمين
ببعض الأفكار
عن نظرية
العدد مثل
الأعداد
الأولية القواسم
والمضاعفات
وغيره حتى
يقدروا على مساعدة
تلاميذهم على
فهم موضوعات في
رياضيات المرحلة
الابتدائية
فهو يحتاج إلى
القاسم المشترك
الأكبر
لكتابة
الكسور في
أبسط صورة و
إلى المضاعف
المشترك
الأصغر
لتوحيد
المقامات في
جمع وطرح
الكسور
الأهداف:
1.
أن
يعطي الطالب
تعريفاً
لمفهوم العدد
الأولي .
2.
أن
يوضح الطالب
مفهوم العدد
الأولي
باستخدام
مكعبات دينز.
3
. أن يوضح
الطالب كيفية
إيجاد قواسم
عدد معين باستخدام
مكعبات دينز.
4
.أن يوضح
الطالب كيفية
إيجاد القاسم
المشترك
الأكبر
لعددين أو
أكثر
باستخدام
مكعبات دينز.
5 .أن يذكر
الطالب مسائل
تطبيقية علي
القاسم المشترك
الأكبر.
6 .أن
يستخدم
الطالب
مكعبات دينز
لإيجاد عدد
معين من
مضاعفات عدد
ما
7
.أن يستخدم
الطالب
مكعبات دينز
لإيجاد
المضاعف
المشترك
الأصغر
لعددين أو أكثر
8
.أن يستخدم
الطالب
مكعبات دينز
لإيجاد
مضاعفات
العشرة
ومضاعفات المئة
9
.أن يذكر
الطالب مسائل
تطبيقية علي
المضاعف المشترك
الأصغر
10.أن
يشرح الطالب
عملية إيجاد
القاسم
المشترك
الأكبر
والمضاعف
المشترك
الأصغر
للعددين بأكثر
من طريقة.
11.أن
يشرح الطالب
عملية إيجاد
المضاعف
المشترك
الأصغر
لعددين عند
معرفة
قاسمهما
المشترك الأكبر
الوسائل
التعليمية :
مكعبات
دينز -
مذكرة الوحدة
الدراسية
المقترحة -
السبورة
العرض
:
الأعداد
الأولية
الأعداد
الأولية هي
الأعداد التي
يقسمها عددان
فقط بدون باق
والعددان هما
العدد واحد والعدد
نفسه ,أو نقول
ان العدد
الأولي هو
العدد الذي له
عاملان فقط
ومختلفان
وهما الواحد
والعدد نفسه.
مع ملاحظة ان
العدد واحد
ليس أوليا لأن
له قاسم واحد
فقط وان العدد
2 هو العدد
الزوجي
الأولي
الوحيد
يمكن
تقديم مفهوم
العدد الأولي
باستخدام مكعبات
دينز
بأنه العدد
الذي لا يمكن
منه بناء سوى
مستطيل واحد
فقط بعداه
الواحد
والعدد نفسه .
ويمكن تدريس
الأعداد
الأولية
باستخدام
مكعبات دينز
وذلك عن طريق
بناء اكبر عدد
ممكن من
المستطيلات
المختلفة من
مكعبين
وثلاثة
مكعبات وأربعة
وهكذا
فالأعداد
التي لا يمكن
بناء أكثر من
مستطيل واحل
لكل عدد ,
بعداه العدد
نفسه والواحد
تسمى الأعداد
الأولية
مثل
5,3,2
![]()
![]()
![]()
2
3
5
أما
الأعداد التي
يمكن أن نبني
منها أكثر من
مستطيل فهي
أعداد ليست
أولية
مثل
9,6,4
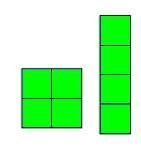
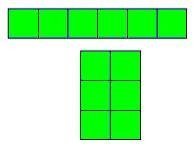
4×1
, 2×2
6×1
,3×2
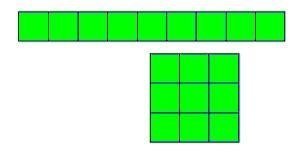
1×9 ,3×3
القواسم
( العوامل) والقاسم
المشترك
الأكبر
قواسم
عدد ( أو
عوامله)
هي الأعداد
التي تقسمه
دون باق
يمكن
دراسة قواسم
العدد بطريقة
ملموسة باستخدام
مكعبات دينز
وذلك عن طريق
بناء
مستطيلات
مختلفة بعدد
من المكعبات
تساوي العدد
المراد إيجاد قواسمه
وتسجيل بعدي
المستطيل في
كل مرة حيث ان
أبعاد
المستطيلات
المتكونة هو
قواسم العدد
فلإيجاد
قواسم العدد 6
تستخدم 6
وحدات
لبناء اكبر
عدد ممكن من
المستطيلات
وتسجيل بعدي
المستطيل في
كل مرة
نلاحظ
أننا نستطيع
بناء
مستطيلين
أبعادهما
(
1×6)

(
2×3)
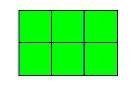
فالعدد
6 قواسمه
هي 6,3,2,1
مع
ملاحظة ان
المستطيل (
2×3) هو
نفسه
المستطيل (
3×2)
وللتأكد يمكن
مقارنتهما
بوضع أحدهما
فوق الآخر

بالمثل
تستخدم 12
مكعبا لإيجاد
قواسم العدد 12
وذلك ببناء
اكبر عدد ممكن
من
المستطيلات
المختلفة على
النحو التالي

(
1×12)
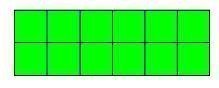
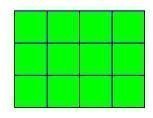
(
2× 6)
( 3×4)
إذن
أبعاد المستطيلات
السابقة هي
(
1×12) ( 2× 6) (
3×4)
قواسم
العدد 12 هي 12,6,4,3,2,1
لإيجاد
قواسم عدد
نكتب كل
عمليات الضرب
التي ناتجها
العدد نفسه.
العوامل التي
تظهر هي قواسم
العدد.
القاسم
المشترك
الأكبر
يمكن
إيجاد القاسم
المشترك
الأكبر
لعددين أو
أكثر
باستخدام
مكعبات دينز
وذلك عن طريق
إيجاد قواسم
كل عدد,
ومن ثم تحديد
القواسم
المشتركة
بينهم وتحديد
القاسم
المشترك
الأكبر بينهم
فمثلا
لإيجاد
القاسم
المشترك
الأكبر للعددين
6 , 9
نوجد
قواسم العدد 6
ببناء اكبر
عدد ممكن من
المستطيلات
من 6 وحدات
وتسجيل بعدي
المستطيل في كل
مرة

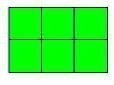
(
1×6)
( 2×3)
نلاحظ
ان قواسم
العدد 6 هي 6,3,2,1
وبالمثل
بالنسبة
للعدد 9 حيث
نقوم ببناء
المستطيلات
التالية


(1
× 9) (3× 3)
ومنه
قواسم العدد 9
هي 9,3,1
القواسم
المشتركة بين
العددين هي3,1
والقاسم
المشترك
الأكبر
للعددين 3
القواسم
المشتركة
لعددين هي
الأعداد التي
يقسم كل واحد
منها هذين
العددين
وأكبرها يسمى القاسم
المشترك
الأكبر.
مسائل
تطبيقية علي
القاسم
المشترك
الأكبر
1 ) دلة
للقهوة تسع 48سل ,
وإبريق للشاي
يسع 72
سل , نريد أن
نسكب كلاً من
القهوة
والشاي في
أكواب لها
السعة نفسها .
ما عدد
الأكواب
المستخدمة
إذا كانت سعة
الكوب الواحد
هي أكبر سعة ؟
2 )
أراد شخص أن
يوزع 540 كغم من
الأرز , و280 كغم من
السكر على عدد
من الأسر , ما
أكبر عدد من الأسر
ممكن توزيع
الأرز والسكر
عليها بالتساوي
؟ وما
نصيب كل أسرة
من كلا
النوعين ؟
3)
لفٌتان من
القماش
طولاهما : 84 م , 60 م ,
قصصنا اللفتين
إلى قطع
متساوية
الطول.
ما طول القطعة
الواحدة ؟
وما عدد قطع
كل من اللفتين
؟
4 ) بنى
متعهد بناءين
, ارتفاعهما : 20 م
, 24 م معتمداً الشرطين
التاليين
- طوابق
البناءين
لهما
الارتفاع
نفسه .
- اعتماد
أقل عدد ممكن
من الطوابق .
ما
ارتفاع
الطابق ؟
وما عدد
الطوابق في كل
من البناءين ؟
المضاعفات
والمضاعف
المشترك
الأصغر
يستخدم
الأطفال فكرة
المضاعف
عندما يبدأون
في التفكير في
الجمع
المتكرر
والضرب ,
فمثلا
كل من الأعداد
10,8,6,4,2,مضاعفات
العدد اثنين وبالمثل
12,9,6,3 مضاعفات
العدد 3
يمكن
إيجاد عدد من
مضاعفات عدد
معين باستخدام
مكعبات دينز
ببناء
مستطيلات
مختلفة على أن
يكون احد بعدي
كل مستطيل هو
العدد المطلوب
إيجاد
مضاعفاته
والبعد الآخر
يمثل رقم المضاعف
( أي
المضاعف
الأول
والثاني
وهكذا )للعدد
المطلوب
إيجاد
مضاعفاته
بينما عدد
المكعبات تمثل
المضاعف
فالمضاعف
الرابع للعدد
3 هو مستطيل
احد بعديه 4
والآخر 3
وبالتالي
يتكون من12
مكعب أي أن
المضاعف
الرابع للعدد
3 هو 12
ولإيجاد
المضاعفات
الأربعة
الأولى للعدد
3 نبني
مستطيلات
مختلفة على أن
يكون احد بعدي
المستطيل 3
مكعبات
والبعد الآخر
(4,3,2,1) يمثل
رقم المضاعف
وعدد
المكعبات في
كل مستطيل
تمثل المضاعف
على النحو
التالي
![]()

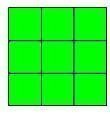

3×1
3×2
3×3
3×4
فالمضاعف
الأول 3×1=3
مكعبات
والمضاعف
الثاني 3×2=6
مكعبات
والمضاعف
الثالث 3×3=9
مكعبات
والمضاعف
الرابع 3×4=12
مكعب
مضاعفات
العدد 3 هي 12,9,6,3
وبالمثل
يمكن إيجاد
مضاعفات
العدد 4
كالتالي
![]()



4×1
4×2 4×3
4×4
مضاعفات
العدد 4 هي 16,12,8,4
نحصل
على مضاعفات
عدد عندما
نضربه بكل من
الإعداد
الصحيحة 1, 2, 3, ....
المضاعف
المشترك
الأصغر
يمكن
إيجاد
المضاعف
المشترك
الأصغر
لعددين أو
أكثر
باستخدام
مكعبات دينز
بإيجاد عدد من
المضاعفات
الأولى لكل
عدد حتى يتم
الحصول على
مضاعف مشترك,
فلإيجاد
المضاعف
المشترك
الأصغر
للعددين 5,3
يتم
إيجاد مضاعف
العدد 3 على
النحو التالي
![]()



3×1
3×2
3×3
3×4

3×5
مضاعف
العدد 3 هو 15,12,9,6,3
وبالمثل
مضاعفات
العدد 5



5×1
5×2
5×3
وهي
15,10,5
ومنه
المضاعف
المشترك
الأصغر
للعددين هو 15
أما
مضاعفات
العشرة فيمكن
تمثيلها
بالأصابع
فالمضاعف
الأول للعشرة
يمثل بإصبع
![]()
10
والمضاعف
الثاني بإصبعين
والثلاثة
بثلاثة أصابع
وهكذا


20
30
40
ومضاعفات
100 تمثل
بالمربعات
فالمربع يمثل
المضاعف
الأول 100
ومربعين
يمثلان
المضاعف
الثاني لـ 100 وهكذا



100
200
300
مسائل
تطبيقية علي
المضاعف
المشترك
الأصغر
1
) ثلاثة
من الطلاب
تقابلوا عند
الطبيب , فطلب
من الأول
مراجعته كل 5
أيام ومن
الآخر كل 4
أيام ومن
الثالث كل 3
أيام .
والمطلوب
معرفة الموعد
الذي
يتقابلون فيه
للمرة
الثانية.
2
) بدأ
طالبان
الدوران حول
مضمار , إذا
كان الأول
يستغرق 8
دقائق
للدوران دورة
كاملة , بينما
يستغرق الثاني
6 دقائق , فبعد
كم دقيقة
يلتقيان عند
نقطة
البداية؟
3
) يمكننا
قص حبل إلي
عدد صحيح من
القطع وذلك في
إحدى
الحالتين
-
إذا كان طول
القطعة
الواحدة 12 م .
-
إذا كان طول
القطعة
الواحدة 16 م .
ما
طول أقصر حبل
يحقق الشرطين
أعلاه؟
4
) قرر أحد
المطاعم في
يوم افتتاحه
منح وجبة إفطار
مجانية لمن
يحمل الأرقام ( 5 , 10 ,
15 , ....)
ووجبة عشاء
مجانية لحامل
الأرقام (
12 , 24 , 36 , ...) ما
رقم أول شخص
يحصل على
الوجبتين ؟
إيجاد
القاسم
المشترك
الأكبر
والمضاعف المشترك
الأصغر للعددين
يمكن
إيجاد القاسم
المشترك
الأكبر
والمضاعف
المشترك
الأصغر
للعددين 35 , 60
بالطرق
التالية:
1) نحلل
العدد 35 إلى
عوامله
الأولية
كالتالي
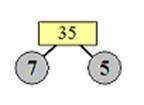
العوامل
الأولية
للعدد 35 هي : 5 , 7
ثم
نكتب نتيجة
التحليل كما
يلي
35
= 5 × 7
ثم
نحلل العدد 60
عوامله
الأولية بأي
من الطرق التالية:
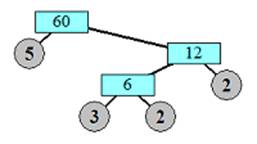

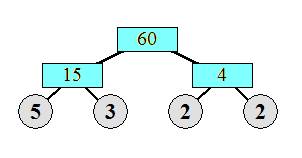


العوامل
الأولية
للعدد 60 هي : 2, 3 , 5
ثم
نكتب نتيجة
التحليل كما
يلي
60
= 2 × 2 × 3 × 5
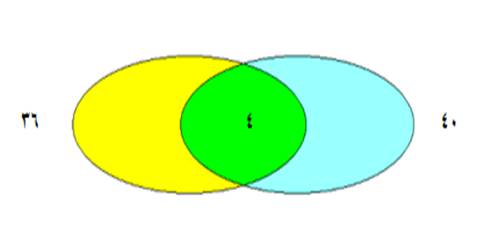
نلاحظ
أن هناك عوامل
مشترك بين
العددين وعوامل
خاصة لكل عدد
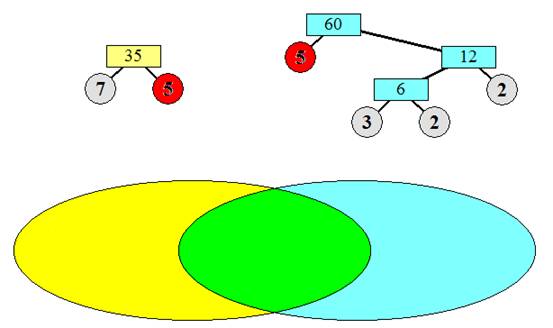
المجموعة
الزرقاء تمثل
عوامل العدد 60
والمجموعة
الصفراء تمثل
عوامل العدد35
أما العوامل
المشتركة
بينهما
فيمثله تقاطع المجموعتين
وهي المجموعة
الخضراء


القاسم
المشترك
الأكبر
للعددين 35 , 60 هو 5
المضاعف
المشترك
الأصغر
للعددين 35 , 60 هو 2 × 2 × 3 × 5 × 7 = 420
2
)
ويمكن
إيجاد القاسم
المشترك
الأكبر و
المضاعف
المشترك
الأصغر للعددين35
, 60 بالطريقة
التالية:
|
60 |
35 |
5 |
|
12 |
7 |
|
نتوقف
لأن ليس
بينهما قاسم
مشترك غير
الواحد
5
القاسم
المشترك
الأكبر
للعددين 35 و 60
12 × 7 × 5 = 420
المضاعف
المشترك
الأصغر
للعددين 35 و 60
مع
ملاحظة انه
يمكن تعميم القاعدة
السابقة على
ثلاثة أعداد
أو أكثر علي النحو
التالي
|
12 |
18 |
16 |
2 |
|
6 |
9 |
8 |
|
حيث
2 قاسم مشترك
للأعداد
الثلاثة
ولأنه لا يوجد
قاسم مشترك
آخر للأعداد
الثلاثة نبحث
عن قاسم مشترك
لعددين لنجد
أن العدد 2
قاسم مشترك
للعددين 6
و 8 مع
إبقاء العدد
الآخر كما هو وهو 9
|
12 |
18 |
16 |
2 |
|
6 |
9 |
8 |
2 |
|
3 |
9 |
4 |
|
ثم
نلاحظ انه
يوجد قاسم
مشترك بين 9 و 3 وهو
3
|
12 |
18 |
16 |
2 |
|
6 |
9 |
8 |
2 |
|
3 |
9 |
4 |
3 |
|
1 |
3 |
4 |
|
إذن
المضاعف
المشترك
الأصغر
للأعداد
الثلاثة هو 3 ´ 4 ´ 3 ´ 2 ´ 2 =144
وباستخدام
أشكال
فن وبتحليل
كل عددين مع
بعض نلاحظ أن
|
12 |
16 |
2 |
|
16 |
18 |
2 |
|
12 |
18 |
2 |
|
6 |
8 |
2 |
|
8 |
9 |
|
|
6 |
9 |
3 |
|
3 |
4 |
|
|
|
|
|
|
2 |
3 |
|
نلاحظ
أن 2 قاسم
مشترك
للأعداد
الثلاثة لذلك
نضعه في منطقة التقاطع
للدوائر
الثلاث
ونلاحظ
أن العدد 3
قاسم مشترك
للعددين 18 و 12
لذلك نضعه في
منطقة تقاطعهما
ونلاحظ
أن العدد 2
قاسم مشترك
للعددين 16 و 12
لذلك نضعه في
منطقة تقاطعهما
في
الدائرة التي
تمثل 16 يوجد بها 2 × 2
= 4 لذلك
تكتب في الجزء
الخاص بها
4 ليصبح 2 × 2 × 4 =16
بالمثل
في الدائرة
التي تمثل 18
يوجد بها 2 × 3 إذن هي
تحتاج إلي 3
ليصبح
المجموع 18
أما
الدائرة التي
تمثل 12 يوجد بها 2 × 2
× 3 =12
والشكل
التالي يوضح
الفكرة
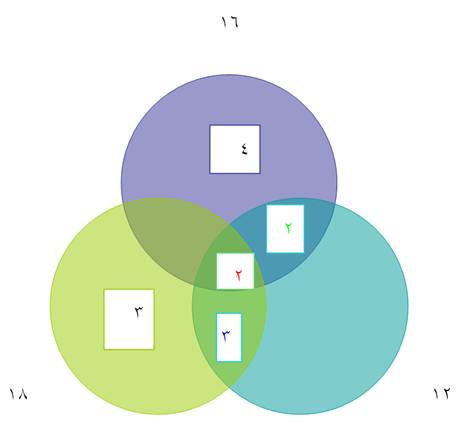
حيث
المضاعف
المشترك هو
حاصل ضرب
الأعداد التي
داخل الدوائر
4
´ 2´ 2´ 3´ 3 =144
أو
نقول 2
قاسم مشترك
للإعداد
الثلاثة

وبقسمة
كل عدد خارج
الدوائر (
18 , 16 , 12 ) علي 2 نحصل
علي ( 9,
8 , 6 )ونكتب
نتيجة القسمة
خارج الدوائر
بالشكل التالي:
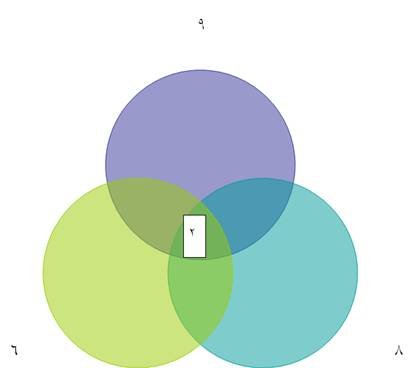
وبالنظر
للأعداد خارج
الدوائر
نلاحظ أن هناك
قاسم مشترك
بين 9 و 6 وهو 3
كما
يوجد قاسم
مشترك بين 6 و 8
وهو 2
لذلك
نأخذ احد هذين
القاسمين
وليكن 3 ونضعه
في منطقة
تقاطع
الدائرتين
اللتين
يمثلان 9و 6
ونكتب نتيجة
قسمة كل عدد
منهما ( 9 و6 ) علي
3 خارج
الدائرة علي
النحو التالي

وبالمثل
بالنسبة
للعددين 2و
8 حيث يوجد
قاسم مشترك
بينهما وهو
العدد
2
حيث
يمثل العدد 2
في منطقة
تقاطعهما ونتيجة
قسمتهما علي 2
خارج الدائرة
علي النحو التالي:

وبضرب
الأعداد داخل
الدائرة
وخارجها نحصل
علي المضاعف
المشترك
الأصغر
مع
ملاحظة انه لو
أخذنا في
الخطوة
الثانية القاسم
المشترك
للعددين 6و
8 بدلاً من
القاسم
المشترك
للعددين 6و9
لحصلنا علي
نفس النتيجة
وهي كالتالي

حيث
2 قاسم مشترك
للعددين 6و8
لذلك نضعه في
تقاطع
الدائرتين
اللتين تمثلهما
وخارج كل
دائرة نتيجة
قسمة كل منهما
علي 2 والشكل
التالي يوضح
ذلك
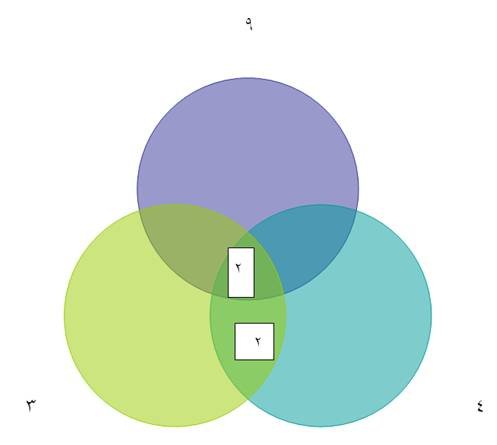
وبالمثل
بالنسبة لـ 9 و 3
وبالمثل
|
24 |
27 |
18 |
3 |
|
8 |
9 |
6 |
2 |
|
4 |
9 |
3 |
3 |
|
4 |
3 |
1 |
|
المضاعف
المشترك
الأصغر
للإعداد هو 4 ´ 3 ´ 3 ´ 2 ´ 3 = 216
وباستخدام
أشكال فن

المضاعف
المشترك
الأصغر هو 3 ´ 3´ 3´ 2 ´ 4 = 216
أو
نقول نكتب
الأعداد
المراد إيجاد قواسمها
كالتالي
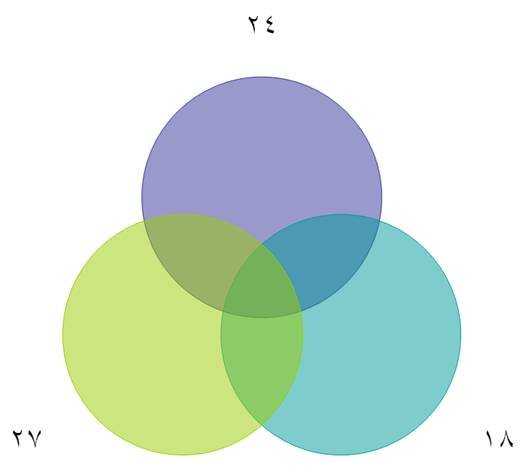
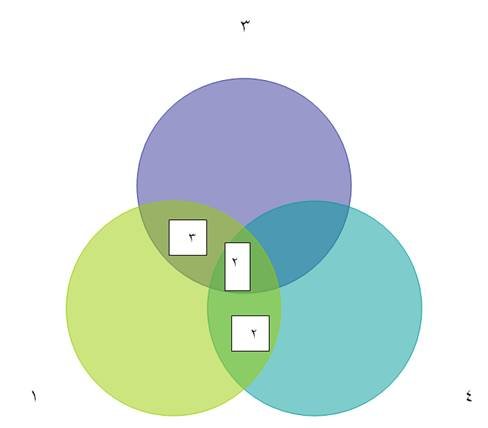
يكتب
القاسم
المشترك
للأعداد
الثلاثة داخل تقاطع
الثلاث
دوائر مع
كتابة حصل قسمة
كل عدد عليه
خارج الدائرة
كالتالي
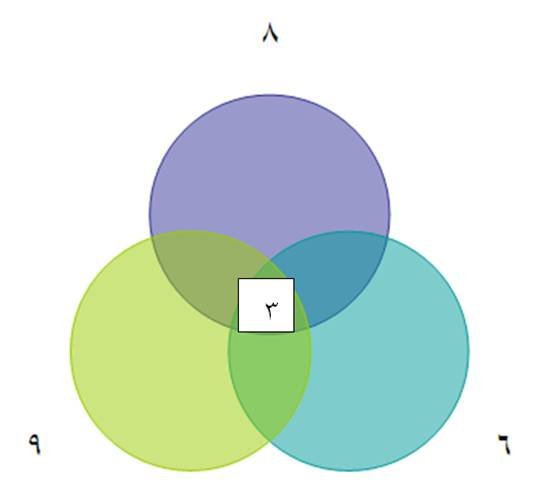
ثم
يبحث عن قاسم
مشترك لعددين
ويكتبه
داخل تقاطع
الدائرتين
التي
تمثلهما وحاصل
القسمة خارج
الدائرة
إما ان
يختار 6و 8 أو 9 و6
ففي هذه
الحالة نختار 6و8

والمثل
بين العددين 3و9

وبضرب
الأعداد داخل
الدوائر
وخارجها نحصل
علي المضاعف
المشترك
الأصغر
والمثل
لإيجاد
القاسم
المشترك
الأكبر والمضاعف
المشترك
الأصغر
للعددين 36 , 40
1)

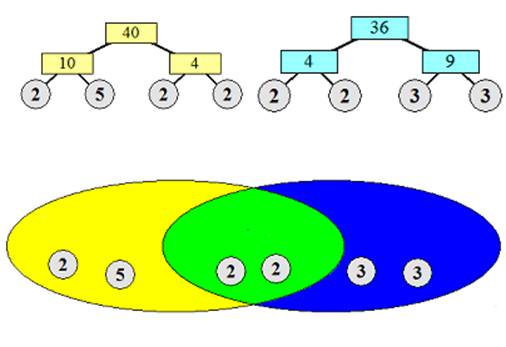
نلاحظ
أن القاسم
المشترك
الأكبر
للعددين هو 2 × 2 = 4
والمضاعف
المشترك
الأصغر
للعددين هو 3 × 3 × 2 × 2 × 5 × 2 = 360
2
)
ويمكن
إيجاد القاسم
المشترك
الأكبر و
المضاعف
المشترك
الأصغر للعددين35
, 60 في خطوة
واحدة
بالطريقة
التالية:
|
40 |
36 |
2 |
|
20 |
18 |
2 |
|
10 |
9 |
|
نتوقف
لأن ليس
بينهما قاسم
مشترك غير
الواحد
2 × 2 = 4
القاسم
المشترك
الأكبر للعددين
36 و 40
10×
9 × 2 × 2 = 360
المضاعف
المشترك
الأصغر
للعددين 36 و 40
3
)
ويمكن
إيجاد القاسم
المشترك
الأكبر و
المضاعف
المشترك الأصغر
للعددين35 ,
60 بالطريقة
التالية:
نحلل
العددين إلى
عواملهما
الأولية
كالتالي :
|
36 |
2 |
|
|
18 |
2 |
|
|
9 |
3 |
|
|
3 |
3 |
|
|
1 |
|
|
|
2 2 |
||
|
36 = 2 × 3 |
||
|
40 |
2 |
|
20 |
2 |
|
10 |
2 |
|
5 |
5 |
|
1 |
|
|
3 |
|
40 = 2 × 5 |
وحيث
أن
القاسم
المشترك
الأكبر
لعددين هو
حاصل ضرب قوى
العوامل
الأولية
المشتركة فقط
والتي لها الأس
الأصغر
و
المضاعف
المشترك
الأصغر
لعددين هو
حاصل ضرب قوى
العوامل
الأولية
للعددين
والتي لها
الأس الأكبر
وعلية
فان المضاعف
المشترك
الأصغر
للعددين 40 , 36 هو
|
2
3 |
|
3 × 2 × 5 |
=
9 ×
8 × 5
=
360
والقاسم
المشترك
الأكبر
للعددين 40 , 36 هو
|
2 |
|
2 |
=
4
ولتوضيح
إيجاد القاسم
المشترك
الأكبر لعددين
بوجود أكثر من
عامل أولي
مشترك نأخذ
العددين 36 , 90
حيث
نحلل العدد 90
|
90 |
2 |
|
|
45 |
3 |
|
|
15 |
3 |
|
|
5 |
5 |
|
|
1 |
|
|
|
2 |
|
||
|
90 = 2 ×
3 ×5 |
|
||
القاسم
المشترك
الأكبر
لعددين هو
|
2 1 |
|
3 ×
2 |
=
9 × 2
=
18
4
)
كما
يمكن إتباع
الطريقة
التالية
لإيجاد
المضاعف
المشترك
الأصغر
للعددين 40 , 36
-
نحلل العددين
سوياً كما يلي
:
-
نحدد أصغر عدد
أولي يقسم أحد
العددين على
الأقل.
-
نكتب ناتج
القسمة
الممكنة
ونحافظ على
العدد الذي لا
يقبل القسمة .
- نكرر
العملية حتى
نحصل على : 1 , 1
|
36 |
40 |
2 |
|
18 |
20 |
2 |
|
9 |
10 |
2 |
|
9 |
5 |
3 |
|
3 |
5 |
3 |
|
1 |
5 |
5 |
|
1 |
1 |
|
\المضاعف
المشترك
الأصغر
للعددين هو : 2 ×
2 × 2 × 3 × 3 × 5 = 360
إيجاد
المضاعف
المشترك
الأصغر
لعددين عند معرفة
قاسمهما
المشترك
الأكبر
1
-
باستخدام
أشكال فن (Vinn diagrams)
يمكن
تمثيل القاسم
المشترك
الأكبر
للعددين 40 , 36 في
منطقة
التقاطع لدائرتين
احدهما تمثل
العدد الأول
والأخرى تمثل
العدد الثاني
كالتالي :
خارج
قسمة العدد
الأول على
القاسم
المشترك الأكبر
يكتب داخل
الدائرة
الأولى ,
وخارج قسمة
العدد الثاني
على القاسم
المشترك
الأكبر يكتب
داخل الدائرة
الثانية كما
يلي :

حاصل
ضرب الأعداد
الثلاثة التي
داخل الدائرتين
هو المضاعف
المشترك
الأصغر
للعددين 36,40
وعليه
فان المضاعف
المشترك
الأصغر
للعددين 40 , 36 هو 10 × 4 × 9 = 360
2
- هناك
طريقة حسابية
مجردة يمكن بها إيجاد
المضاعف
المشترك
الأصغر
لعددين عند معرفة
قاسمهما
المشترك
الأكبر في
المعادلة التالية
:
حاصل
ضرب العددين = القاسم
المشترك الأكبر×
المضاعف المشترك
الأصغر
مما
يعني أن
المضاعف
المشترك
الأصغر =
حاصل ضرب
العددين ÷
القاسم
المشترك
الأكبر
وعليه
فان
المضاعف
المشترك
الأصغر للعددين
40, 36
=
( 36 × 40 ) ÷ 4
=
360
التقويم
1.
أعط
تعريفاً
لمفهوم العدد
الأولي ؟
2.
وضح مفهوم
العدد الأولي
باستخدام مكعبات
دينز؟
3.
.
وضح
كيفية إيجاد
قواسم عدد
معين باستخدام
مكعبات دينز؟
4.
.وضح كيفية
إيجاد القاسم
المشترك الأكبر
لعددين أو
أكثر
باستخدام
مكعبات دينز؟
5.
.أذكر
مسائل
تطبيقية علي
القاسم
المشترك الأكبر؟
6.
.استخدم
مكعبات دينز
لإيجاد عدد
معين من
مضاعفات عدد
ما؟
7.
.استخدم
مكعبات دينز
لإيجاد
المضاعف
المشترك
الأصغر
لعددين أو
أكثر؟
8.
.استخدم
مكعبات دينز
لإيجاد
مضاعفات
العشرة
ومضاعفات المئة؟
9.
.أذكر
مسائل
تطبيقية علي
المضاعف
المشترك الأصغر؟
10..اشرح عملية
إيجاد القاسم
المشترك الأكبر
والمضاعف
المشترك
الأصغر
للعددين بأكثر
من طريقة؟
11..اشرح عملية
إيجاد المضاعف
المشترك
الأصغر
لعددين عند
معرفة قاسمهما
المشترك
الأكبر؟